Mathematics P1 Past Paper FEBRUARY/MARCH 2016 - GRADE 12 NATIONAL SENIOR CERTIFICATE
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS P1
FEBRUARY/MARCH 2016
MARKS: 150
TIME: 3 hours
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs et cetera that you have used in determining your answers.
- Answers only will not necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of this question paper.
- Write neatly and legibly.
QUESTION 1
1.1 Solve for x:
1.1.1 x2 -x-12 = 0 (3)
1.1.2 x(x+3) -1 = 0 (Leave your answer in simplest surd form.) (3)
1.1.3 x(4- x)<0 (3)
1.1.4
x = a2+a-2 if a = 888 888 888 888 (2)
a-1
1.2 Solve the following equations simultaneously:
y + 7 = 2x and x2 - Xy+3y2 =15 (6)
1.3 Determine the range of the function y = x+ 1/x, x≠0 and x is real (6)
[23]
Question 2
2.1 Given the following quadratic sequence: -2;0:3; 7;...
2.1.1 Write down the value of the next term of this sequence. (1)
2.1.2 Determine an expression for the nth term of this sequence. (5)
2.1.3 Which term of the sequence will be equal to 322? (4)
2.2
Consider an arithmetic sequence which has the second term equal to 8 and the fifth term equal to 10
2.2.1 Determine the common difference of this sequence. (3)
2.2.2 Write down the sum of the first 50 terms of this sequence, using sigma notation. (2)
2.2.3 Determine the sum of the first 50 terms of this sequence.(3)
[18]
QUESTION 3
Chris bought a bonsai (miniature tree) at a nursery. When he bought the tree, its height was 130 mm. Thereafter the height of the tree increased, as shown below.
| INCREASE IN HEIGHT OF THE TREE PER YEAR | ||
| During the first year | During the second year | During the third year |
| 100 mm | 70 mm | 49 mm |
3.1
Chris noted that the sequence of height increases, namely 100 ; 70: 49 ..., was geometric. During which year will the height of the tree increase by approximately 11,76 mm? (4)
3.2 Chris plots a graph to represent the height h(n) of the tree (in mm) n years after he bought it. Determine a formula for h(n). (3)
3.3 What height will the tree eventually reach? (3)
[10]
QUESTION 4
Given: f(x)=2-x +1
4.1 Determine the coordinates of the y-intercept of f. (1)
4.2 Sketch the graph of f, clearly indicating ALL intercepts with the axes as well as any asymptotes. (3)
4.3 Calculate the average gradient of f between the points on the graph where x = -2 and x= 1. (3)
4.4 If h(x)=3f(x), write down an equation of the asymptote of h.
[8]
QUESTION 5
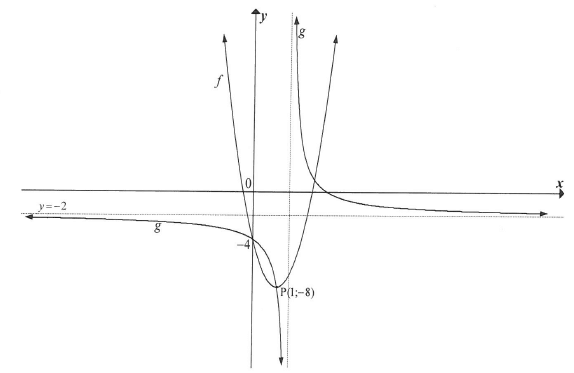
The graphs of the functions f(x) = a(x + p)2 + q and g(x)=k/(x+r) + d
are sketched below.
Both graphs cut the y-axis at - 4. One of the points of intersection of the graphs is P(1 ;-8), which is also the turning point of f. The horizontal asymptote of g is y=-2.
5.1 Calculate the values of a, p and q. (4)
5.2 Calculate the values of k, r and d. (6)
5.3 Determine the value(s) of x in the interval x≤1 for which g(x)≥f(x). (2)
5.4 Determine the value(s) of k for which f(x) = k has two, unequal positive roots. (2)
5.5 Write down an equation for the axis of symmetry of g that has a negative gradient. (3)
5.6 The point P is reflected in the line determined in QUESTION 5.5 to give the point Q. Write down the coordinates of Q. (2)
[19]
QUESTION 6
Given: f(x) = 1/4x2, x ≤ 0
6.1 Determine the equation of f-1 in the form f-1(x) = ... (3)
6.2 On the same system of axes, sketch the graphs of f and f-1. Indicate clearly the intercepts with the axes, as well as another point on the graph of each of f and f-1 (3)
6.3 Is f-1 a function? Give a reason for your answer. (2)
[8]
QUESTION 7
7.1 Diane invests a lump sum of R5 000 in a savings account for exactly 2 years. The investment eams interest at 10% p.a., compounded quarterly.
7.1.1 What is the quarterly interest rate for Diane's investment?
7.1.2 Calculate the amount in Diane's savings account at the end of the 2 years. (3)
7.2 Motloi inherits R800 000. He invests all of his inheritance in a fund which earns interest at a rate of 14% p.a., compounded monthly. At the end of each month he withdraws R10 000 from the fund. His first withdrawal is exactly one month after his initial investment.
7.2.1 How many withdrawals of R10 000 will Motloi be able to make from this fund? (5)
7.2.2 Exactly four years after his initial investment Motloi decides to withdraw all the remaining money in his account and to use it as a deposit towards a house.
(a) What is the value of Motloi's deposit, to the nearest rand?
(b) Motloi's deposit is exactly 30% of the purchase price of the house. What is the purchase price of the house, to the nearest rand?
QUESTION 8
8.1 Determine f'(x) from first principles if f(x)=-x2 +4. (5)
8.2 Determine the derivative of:
8.2.1 y = 3x2 +10x (2)
8.2.2 f(x)=(x-3/x)2
8.3 Given: f(x) = 2x3 - 23x2 +80x - 84
8.3.1 Prove that (x-2) is a factor of f. (2)
8.3.2 Hence, or otherwise, factorise f(x) fully. (2)
8.3.3 Determine the x-coordinates of the turning points of f. (4)
8.3.4 Sketch the graph of f. clearly labelling ALL turning points and intercepts with the axes. (3)
8.3.5 Determine the coordinates of the y-intercept of the tangent to f that has a slope of 40 and touches f at a point where the x-coordinate is an integer.(6)
[27]
QUESTION 9
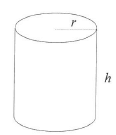
A soft drink can has a volume of 340 cm3, a height of h cm and a radius of r сm.
9.1 Express h in terms of r. (2)
9.2 Show that the surface area of the can is given by A(r) = 2πr2 +680r-1. (2)
9.3 Determine the radius of the can that will ensure that the surface area is a minimum. (4)
QUESTION 10
10.1 Each passenger on a certain Banana Airways flight chose exactly one beverage from tea, coffee or fruit juice. The results are shown in the table below.
| MALE | FEMALE | TOTAL | |
| Tea | 20 | 40 | 60 |
| Coffee | b | c | 80 |
| Fruit juice | d | e | 20 |
| TOTAL | 60 | 100 | a |
10.1.1 Write down the value of a. (1)
10.1.2 What is the probability that a randomly selected passenger is male? (2)
10.1.3 Given that the event of a passenger choosing coffee is independent of being a male, calculate the value of b. (4)
10.2 A Banana Airways aeroplane has 6 seats in each row.
10.2.1 How many possible arrangements are there for 6 people to sit in a row of 6 seats? (2)
10.2.2 Xoliswa, Ances and 4 other passengers sit in a certain row on a Banana Airways flight. In how many different ways can these 6 passengers be seated if Xoliswa and Anees must sit next to each other? (2)
10.2.3 Mary and 5 other passengers are to be seated in a certain row. If seats are allocated at random, what is the probability that Mary will sit at the end of the row? (4)
[15]
Total 150