Mathematics P2 Past Paper FEBRUARY/MARCH 2016 - GRADE 12 NATIONAL SENIOR CERTIFICATE
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS P2
FEBRUARY/MARCH 2016
MARKS: 150
TIME: 3 hours
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs et cetera that you used to determine the answers.
- Answers only will NOT necessarily be awarded full marks.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- An INFORMATION SHEET with formulae is included at the end of the question
paper. - Write neatly and legibly.
QUESTION 1
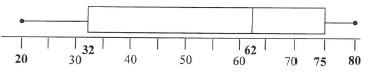
The box and whisker diagram below shows the marks (out of 80) obtained in a History test by a class of nine learners.
1.1 Comment on the skewness of the data, (1)
1.2 Write down the range of the marks obtained. (2)
1.3 If the learners had to obtain 32 marks to pass the test, estimate the percentage of the class that failed the test. (3)
1.4 In ascending order, the second mark is 28, the third mark 36 and the sixth mark 69. The seventh and eighth marks are the same. The average mark for this test is 54.
| 28 | 36 | 69 |
Fill in the marks of the remaining learners in ascending order. (6)
[11]
QUESTION 2
A company recorded the number of messages sent by e-mail over a period of 60 working days. The data is shown in the table below.
| NUMBER OF MESSAGES | NUMBER OF DAYS |
| 10<x<20 | 2 |
| 20<x<30 | 8 |
| 30<x< 40 | 5 |
| 40<x< 50 | 10 |
| 50<x<60 | 12 |
| 60<x< 70 | 18 |
| 70<x< 80 | 3 |
| 80<x<90 | 2 |
2.1 Estimate the mean number of messages sent per day, rounded off to TWO decimal places. (3)
2.2 Draw a cumulative frequency graph (ogive) of the data on the grid provided in the ANSWER BOOK. (4)
2.3 Hence, estimate the number of days on which 65 or more messages were sent. (2)
[9]
QUESTION 3
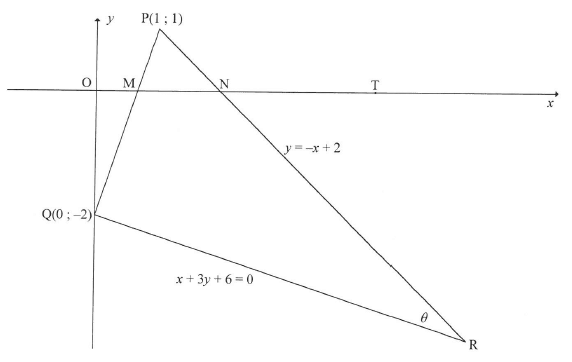
In the diagram below, P(1 ; 1), Q(0;-2) and R are the vertices of a triangle and <PRQ = θ. The x-intercepts of PQ and PR are M and N respectively. The equations of the sides PR and QR are y=-x+2 and x + 3y + 6 = 0 respectively. T is a point on the x-axis, as shown.
3.1 Determine the gradient of QP. (2)
3.2 Prove that PÔR = 90°. (2)
3.3 Determine the coordinates of R. (3)
3.4 Calculate the length of PR. Leave your answer in surd form. (2)
3.5 Determine the equation of a circle passing through P, Q and R in the form (x-a)2 + (y - b)2 =r2 (6)
3.6 Determine the equation of a tangent to the circle passing through P, Q and Rat point P in the form y=mx+c.
3.7 Calculate the size of θ.
QUESTION 4
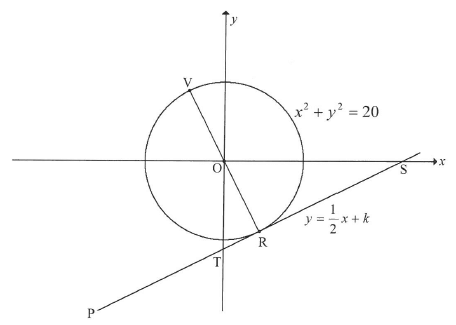
In the diagram below, the equation of the circle with centre O is x2 + y2 = 20. The tangent PRS to the circle at R has the equation y= 1/2x+k. PRS cuts the y-axis at T and the x- axis at S.
4.1 Determine, giving reasons, the equation of OR in the form y = mx + c. (3)
4.2 Determine the coordinates of R. (4)
4.3 Determine the area of OTS, given that R(2;-4). (6)
4.4 Calculate the length of VT. (4)
[17]
QUESTION 5
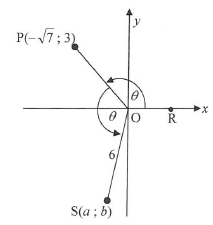
5.1 P(-√7;3) and S(a; b) are points on the Cartesian plane, as shown in the diagram below. POR = POS = θ and OS = 6.
Determine, WITHOUT using a calculator, the value of:
5.1.1 tan θ (1)
5.1.2 sin(-θ) (3)
5.1.3 a
5.2
5.2.1 Simplify 4sinxcosx/(2sin2x - 1) to a single trigonometric ratio. (3)
5.2.2 Hence, calculate the value of WITHOUT using a calculator.(Leave your answer in simplest surd form.)(2)
[13]
QUESTION 6
6.1 Given the equation: sin(x + 60°) + 2cos x = 0
6.1 Show that the equation can be rewritten as tan x = -4 - √3. (4)
6.2 Determine the solutions of the equation sin(x + 60°) + 2cos x = 0 in the interval -180° ≤ x ≤ 180° (3)
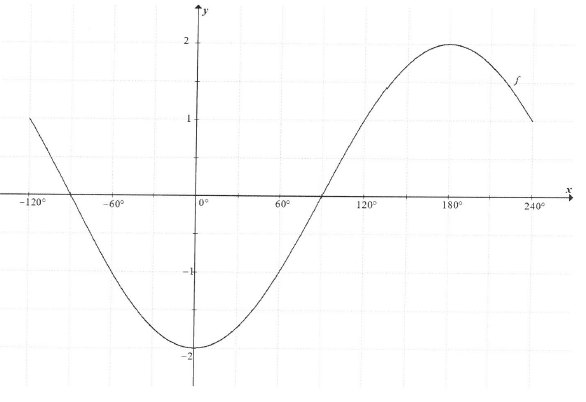
6.3 In the diagram below, the graph of f(x) = -2 cos x is drawn for -120° ≤x ≤ 240°
6.3.1 Draw the graph of g(x) = sin(x + 60°) for -120° ≤x≤ 240° on the grid provided in the ANSWER BOOK. (3)
6.3.2 Determine the values of x in the interval -120° ≤ x ≤ 240o for which sin(x + 60°) + 2cos x > 0.
QUESTION 7
7.1 In the diagram below, ΔPQR is drawn with PQ = 20 - 4x, RQ = x and Q = 60°
7.1.1 Show that the area of ΔPQR = 5√3x - √3x2. (2)
7.1.2 Determine the value of x for which the area of ΔPQR will be a maximum. (3)
7.1.3 Calculate the length of PR if the area of ΔPQR is a maximum. (3)
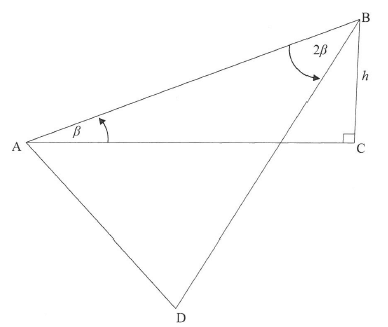
7.2 In the diagram below, BC is a pole anchored by two cables at A and D. A, D and Care in the same horizontal plane. The height of the pole is h and the angle of elevation from A to the top of the pole, B, is β. ABD = 2β and BA=BD.
Determine the distance AD between the two anchors in terms of h. (7)
[15]
Give reasons for ALL statements in QUESTIONS 8, 9 and 10.
QUESTION 8
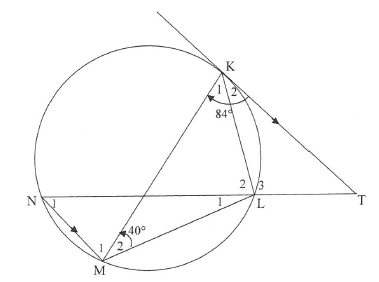
8.1 In the diagram below, tangent KT to the circle at K is parallel to the chord NM. NT cuts the circle at L. ΔKML is drawn. M2, = 40° and MKT = 84o.
Determine, giving reasons, the size of:
8.1.1 K2 (2)
8.1.2 N1 (3)
8.1.3 T (2)
8.1.4 L2 (2)
8.1.5 L1 (1)
8.2 In the diagram below, AB and DC are chords of a circle. E is a point on AB such that BCDE is a parallelogram. DEB = 108° and DAE = 2x + 40°.
Calculate, giving reasons, the value of x. (5)
[15]
QUESTION 9
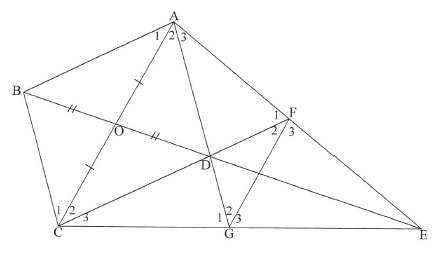
In the diagram below, EO bisects side AC of ΔACE. EDO is produced to B such that BO = OD. AD and CD produced meet EC and EA at G and F respectively.
9.1 Give a reason why ABCD is a parallelogram. (1)
9.2 Write down, with reasons, TWO ratios each equal to ED/DB (4)
9.3 Prove that A1 = F1
9.4 It is further given that ABCD is a rhombus. Prove that ACGF is a cyclic quadrilateral. (3)
[13]
QUESTION 10
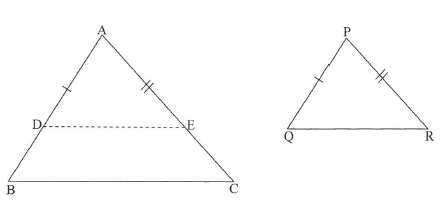
10.1 In the diagram below, ΔABC and ΔPQR are given with A = P, B = Q and Ĉ = R.
DE is drawn such that AD=PQ and AE = PR.
10.1.1 Prove that ΔADE = ΔPQR. (2)
10.1.2 Prove that DE // BC. (3)
10.1.3 Hence, prove that AB/PQ = AC/PR (2)
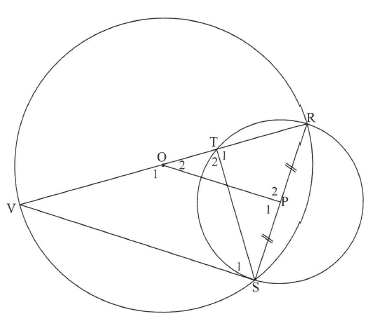
10.2 In the diagram below, VR is a diameter of a circle with centre O. S is any point on the circumference. P is the midpoint of RS. The circle with RS as diameter cuts VR at T. ST, OP and SV are drawn.
10.2.1 Why is OP ⊥ PS? (1)
10.2.2 Prove that ΔROP /// ΔRVS. (4)
10.2.3 Prove that ΔRVS /// ΔRST. (3)
Prove that ST2 = VT. TR. (6)
[21]
TOTAL 150