MATHEMATICAL LITERACY P1
FEBRUARY/MARCH 2016

MARKS: 150

TIME: 3 hours

INSTRUCTIONS AND INFORMATION

1. This question paper consists of FIVE questions. Answer ALL the questions.
2. 
   2.1 Use the ANNEXURES to answer the following questions:
   
   ANNEXURE A for QUESTION 1.2
   ANNEXURE B and ANNEXURE C for QUESTION 3.1
   ANNEXURE C for QUESTION 3.2
   ANNEXURE D for QUESTION 5.2
   
   2.2 Answer QUESTION 5.1.3 on the attached ANSWER SHEET.
   
   2.3 Write your centre number and examination number in the spaces on the ANSWER SHEET. Hand in the ANSWER SHEET with your ANSWER BOOK
3. Number the answers correctly according to the numbering system used in this question paper.
4. Start EACH question on a NEW page.
5. You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
6. Show ALL calculations clearly.
7. Round off ALL final answers appropriately according to the given context, unless stated otherwise.
8. Indicate units of measurement, where applicable.
9. Maps and diagrams are NOT necessarily drawn to scale, unless stated otherwise.
10. Write neatly and legibly.

QUESTION 1

1.1
Audrey started a stokvel on 1 February 2015 to save for the December holidays. She invited 21 friends to join the stokvel. The aim was to continue with the stokvel after 2015.

Guidelines for this stokvel:

• A bank account should be opened and all monies collected should be deposited on the 7 of every month.
• The initial fee to join the stokvel is R250 per member. This initial fee is non-refundable and will be used to continue the stok vel in the future.
• The monthly contribution of each member is R400 and is payable on the 1^st day of every month.
• Members who pay after the 7^th of a month have to pay a fine of 4,75% of the monthly contribution, in addition to the monthly contribution.
• On 20 December 2015 each member will be paid an equal amount of the savings in the account, excluding the initial fees to join, which will be kept in the stokvel account.

During the first meeting all the members paid their initial fees and their first monthly contributions.

1.1.1 Determine the total amount deposited in the bank account after the first meeting. (3)

1.1.2 Lena, a member of the stokvel, had not yet paid her monthly contribution for July by the 7^th.

Calculate the total amount Lena had to pay on 13 July when she made her monthly contribution. (3)

1.1.3 On 20 December 2015 the total amount in the stokvel account was R110 614,84.

Calculate the equal amount that each member received on 20 December 2015, assuming that all the members had paid all their monthly contributions. (4)

1.2 Mrs Mdluli owns fully furnished holiday cottages along the beach. She needs to replace the fridges in 12 of the cottages and obtains a quotation from a furniture store which provides finance. She indicates that she will pay a deposit and agrees to include the extended guarantee, delivery charge and initiation fee as part of the quotation.

ANNEXURE A shows the quotation she received from R&F Finance. Some amounts on the quotation have been omitted.

Use ANNEXURE A to answer the following questions.

1.2.1 Determine the missing value A. (2)

1.2.2 Show how the total value of the goods of R145 787,88 was calculated. (2)

1.2.3 Calculate the percentage deposit that needs to be paid. (3)

1.2.4 Calculate the total VAT amount that is included in the price for ALL the fridges. (3)

1.2.5 Define the term interest in this context.

1.2.6 R&F Finance charges simple interest on their financing deals.

Show how the interest amount of R40 326,29 was calculated. (3)

1.2.7 Calculate the missing value B. (3)

1.2.8 List ALL the extra charges that are not included in this quotation. (3)

1.2.9 Calculate the missing value C. (3)
[34]

QUESTION 2

2.1
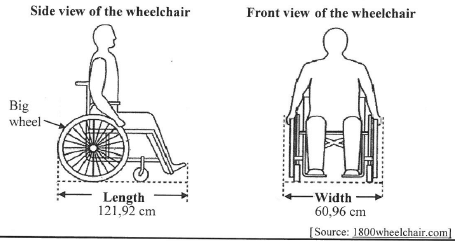
Justin has an injury that requires him to use a wheelchair for a while. He uses the diagrams below to determine certain dimensions of the wheelchair.

Use the diagrams above to answer the following questions,

2.1.1 The outer diameter of the bigger wheel is 54% of the length of the wheelchair.

Determine the length of the outer diameter (rounded off to the nearest mm) of the big wheel. (4)

2.1.2 The big wheel has 24 equally spaced cylindrical spokes attached to the rim, as shown in the picture alongside. The diameter of each spoke is 2 mm. The inner diameter of the rim is 584 mm.

Calculate how far apart the wheel spokes are spaced from each other on the rim.

You may use the following formula:

Circumference of a circle = π x diameter using π = 3,142 (6)

2.1.3 One of the doorway openings in Justin's house is 750 mm wide. Determine, showing ALL calculations, how wide (in mm) the available gap on both sides of the wheelchair is if the wheelchair passes through the doorway opening exactly in the middle.

2.2
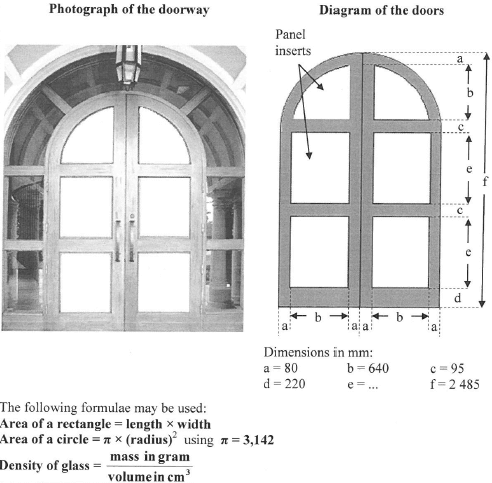
The doorway of a museum is shown in the photograph and diagram below. It has two identical doors that can open to allow for the easy flow of people.

The doors have glass-panel inserts, in the shape of rectangles and quarter circles, embedded in a wooden frame, as shown in the photograph and diagram below.

Use the diagram above to answer the following questions,

2.2.1 Determine the total width, in metres, of the two doors. (3)

2.2.2 Calculate the value of e, the length of the rectangular glass panel inserts. (4)

2.2.3 Calculate the total area (in mm) of ALL the glass-panel inserts. (6)

2.2.4 The total volume of the glass panels is 15 985,408 cm³ and the density of glass is 2,5 g/cm³. Calculate (in kg) the total mass of the glass panels. (4)
[31]

QUESTION 3

3.1
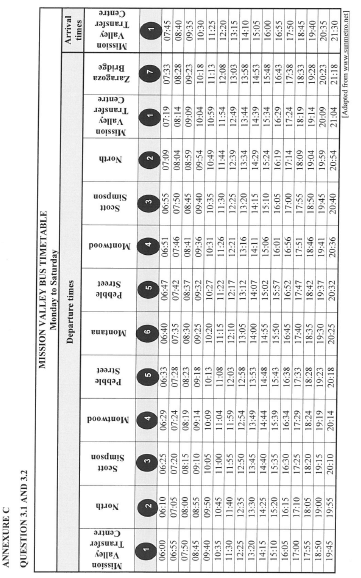
Gonzales lives in Mission Valley and travels by bus to his workplace at the Mission Valley Police Department.

ANNEXURE B shows a route map for the Mission Valley Transfer Centre bus.

The bus route is as follows:

• Starts at the Mission Valley Transfer Centre in George Dieter Street
• Continues along George Dieter Street.
• Turns into Montana Street and then turns into Turner Street (makes a loop).
• Continues back along George Dieter Street.
• Turns into Socorro Street and then turns into Zaragoza Street (makes a loop).
• Ends at the Mission Valley Transfer Centre in George Dieter Street

ANNEXURE C shows a timetable of the Mission Valley Transfer Centre bus. The timetable indicates the time when the bus generally leaves the different bus stops.

Use the route map (ANNEXURE B) and the timetable (ANNEXURE C) to answer the following questions.

3.1.1 Name the bus stop closest to Gonzales's workplace. (2)

3.1.2 Give the general direction of a bus travelling along Turner Street. (2)

3.1.3 Between which TWO bus stops does the route cross only ONE street? (2)

3.1.4 Determine how long it will take a bus to complete a round trip if it departs from the Mission Valley Transfer Centre at 17:55. (2)

3.1.5 Gonzales visited the Department of Human Services. He left the building at 11:52 and arrived at Bus Stop 5 exactly 13 minutes later. Determine how long he had to wait for the next bus to travel directly to Bus Stop 2. (3)

3.1.6 Calculate the time a bus takes to complete the Socorro-Zaragoza loop. (2)

3.2 Use ANNEXURE C to answer the following question.

A bus travelling at an average speed of 43 km/h departs from Bus Stop 3 at 08:15 and arrives at Bus Stop 5 at 08:23.

Calculate the distance, in km, between these two bus stops.

You may use the following formula:
Average speed = ^distance/_time (4)

3.3
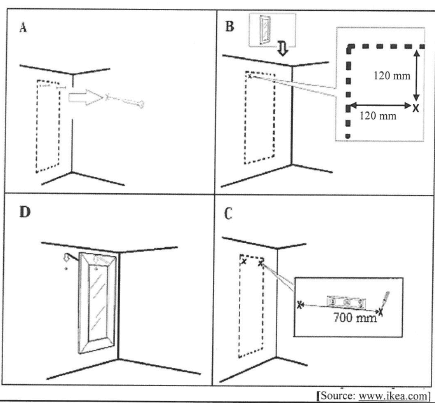
Evelina bought a framed mirror for her room. She wants to mount the mirror on the wall, using two screws. She received the following mounting instructions, diagrams A to D (not in order), with the mirror.

Use the information in the diagrams above to answer the following questions.

3.3.1 Refer to the diagrams and write down the correct order in which the mirror should be mounted. (Use A, B, C and D.) (2)

3.3.2 If written instructions had accompanied the diagrams, match the following instruction with the correct diagram:

Use a pencil and a level to make the second mark, X, exactly 700 mm from the first mark. (2)
[21]

Question 4

Use the information in the table above to answer the following questions.

4.1.1 Identify the municipality that had the highest number of employed people during 2011 (2)

4.1.2 Calculate the difference in the total population of the municipality that had the largest increase in total population from 2001 to 2011.

4.1.3 Calculate the number of elderly people in the Blouberg municipality during 2001.

4.1.4 A person living in the Breede Valley municipality during 2011 is randomly selected. Determine the probability that the person is employed. Express the probability as a common fraction in its simplest form. (3)

4.1.5 Which municipality showed the largest percentage increase in the use of electricity from 2001 to 2011?

4.1.6 Calculate the average population growth rate for the Breede Valley municipality from 2001 to 2011. You may use the following formula:
Average population growth rate =
difference in total population from 2001 to 2011  x  100
       total population in 2001

4.1.7 Calculate, to the nearest km², the land area of the Tlokwe municipality in 2011. (3)

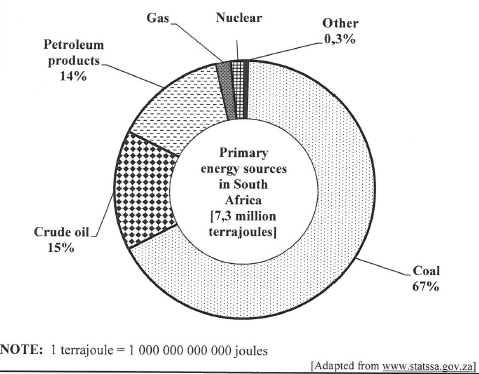
4.2 The natural environment provides resources that drive the economy and other human activities. Statistics SA recently released the 2010 estimates on the primary energy sources available in South Africa, as shown in the pie chart below.

Use the information in the pie chart above to answer the following questions,

4.2.1 Which ONE of the following is exactly the same as 7,3 million terrajoules?

1. 7,3 x 100 000 000 000 000 000 joules
2. 73 000 000 million joules
3. 7 300 000 000 000 000 000 joules
4. 730 000 trillion joules (2)

4.2.2 Calculate the percentage that gas and nuclear resources each contribute to the energy supply if they contribute equally. (3)

4.2.3 Calculate the quantity of energy for petroleum products in terrajoules.

QUESTION 5

5.1
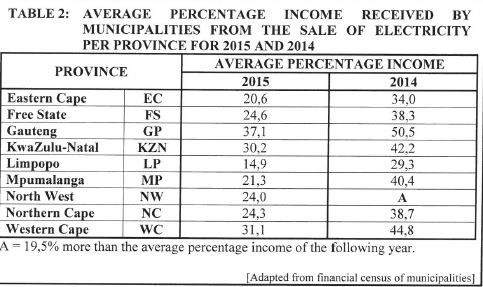
In April 2015 the acting head of Eskom suggested that to improve its financial situation, Eskom should supply electricity directly to all customers. If this should happen many municipalities would lose the income they receive from the sale of electricity.

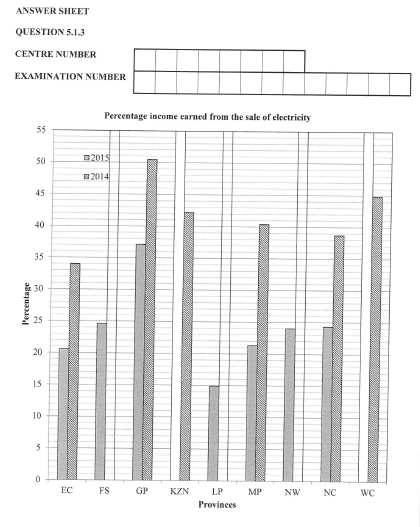
The table below shows the average percentage income received by municipalities from the sale of electricity per province for 2015 and 2014.

A=19,5% more than the average percentage income of the following year.

[Adapted from financial census of municipalities]

Use the table above to answer the following questions.

5.1.1 Arrange, in descending order, the average percentage incomes for 2015. (2)

5.1.2 List ALL the provinces where the municipalities have an average percentage income greater than the mean percentage income for all the provinces during 2015. (5)

5.1.3 Use the information in TABLE 2 to complete the bar graph on the grid provided on the ANSWER SHEET. (7)

5.1.4 Determine the probability (as a percentage) of randomly choosing a province where the average percentage income of the municipalities was not more than 35% for 2014. (3)

5.2

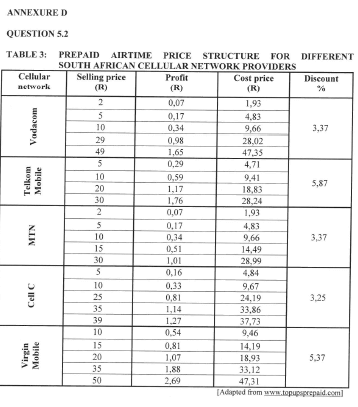
Use ANNEXURE D to answer the following questions.

5.2.1 Determine the probability that Monde sold a Neotel prepaid airtime voucher at one of the schools. (2)

5.2.2 Which cellular network provider offers the second largest percentage discount? (2)

5.2.3 Explain the term profit in this context.

5.2.4 One of the vending machines only sells R15 airtime vouchers. On a particular day MTN airtime worth R270 and Virgin Mobile airtime worth R120 were sold. Calculate the total profit for that day, (4)

5.2.5 Calculate how many school weeks it would take Monde to make a profit of R5 122,50 if his average daily profit is R341,50.

5.2.6 Each vending machine costs R1 539,00, including 14% VAT. Monde bought 52 machines. Determine how many R10 Virgin Mobile airtime vouchers he must sell to cover the total cost of his machines.

5.2.7 If Cell C airtime worth R14 760 is sold, determine the total discount received by Monde. (3)
[37]
TOTAL: 150