FINANCE GRADE 12 NOTES - MATHEMATICAL LITERACY STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- Financial documents
- Till Slips
- Activity 1: Till slip
- Account statements
- Activity 2: Reading an account statement
- Bills
- Activity 3: Municipal bills
- Cell phone bills
- Activity 4: Cell phone bill
- Budgets, income and expenditure statements
- Activity 5: Travel budgets
- Activity 6: Family budget
- Banking, interest and tax
- Bank statements
- Activity 7: Bank statements
- Banking fees
- Activity 8: Calculating banking fees
- Simple interest
- Activity 9: Simple Interest
- Compound interest
- Loans
- Activity 10: Loans
- Inflation
- Activity 11: Inflation
- Payslips, deductions and tax
- Activity 12: Payslips, deductions and tax
Finance
You need to be able to find information from a variety of documents (till slips, account statements and bills). You also need to understand and check the calculations.
Every time you buy an item from a shop, you should receive a till slip. By law, South African till slips must include:
- the name of the shop
- the address of the shop
- the VAT number of the shop
- the words “Tax Invoice”
- the shop’s invoice number
- the date and time of the sale
- a description of the items or services bought
- the amount of VAT charged (14%)
- the total amount payable.
VAT is not charged on some essential groceries in South Africa. These include : paraffin; brown bread; maize meal; samp; mealie rice; dried mealies; dried beans; lentils; tinned sardines; milk powder; milk; rice; vegetables; fruit; vegetable oil and eggs.
Worked example 1
Boiketlo goes to buy groceries at the Sunshine Superette. Study the till slip alongside and answer the questions that follow.
- How did Boiketlo pay for her shopping?
- How much does 1 litre of vegetable oil cost at the Sunshine Superette?
- If there are 6 muffins in the pack of chocolate muffins that Boiketlo bought, how much does each muffin cost?
- What is the last date for a refund and why might Boiketlo need a refund?
- Boiketlo gave the cashier R150,00 and received R19,75
- Calculate what she paid for her
- Why do you think the amount is slightly different to the balance due?
- Why do three items (vegetable oil, brown bread and milk) have stars next to them?
-
- Add up the total of the items which are subject to VAT
- Calculate the VAT (14%) of the total value of these Which letter (A, B, C or D) on the till slip does this correspond to?
- Add the 14% VAT to the total value of the items which are subject to VAT. Which letter (A, B, C, or D) on the till slip does this correspond to?
- Add up the total of the three items that are exempt from VAT. Which letter (A, B, C or D) on the till slip does this correspond to?
- Add together the total (including VAT) of the items that include VAT and the total of the VAT exempt Which letter on the till slip does this correspond to?
Solutions
- She paid with cash.
- 500 mℓ of vegetable oil costs R16,99, so 1 litre costs R16,99 × 2 = R33,98.
- 6 muffins cost R13,95, so one muffin costs R13,95 ÷ 6 = R2,33.
- 27/07/2013. She may need a refund if the food she bought is stale.
-
- R150,00 – R19,75 = R130,25.
- The amount she paid is 2c less than the balance due. The total has been rounded to the nearest multiple of 5c because we no longer use 2c and 1c coins in South Africa.
- The three starred items are exempt from VAT, because they are basic foodstuffs.
-
- R6,95 + R3,95 + R19,99 + R0,44 + R5,49 +R15,99 + R15,99 + R13,95 = R82,75.
- 14% of R82,75 = 82,75 × 0,14 = R11,59: Letter B.
- R82,75 + 11,59 = R94,34: Letter C.
- R16,99 + R6,99 + R11,95 = R35,93: Letter D.
- R94,34 + R35,93 = R130,27: Letter A.
Sakhile goes to his local store and buys some clothes and groceries. He receives the following till slip. Study the slip and answer the questions that follow.
- What item did Sakhile buy on sale, and how much was the discount? (2)
- Can Sakhile return the sale item for refund? Explain your (2)
- How many eggs did Sakhile buy? (1)
- Calculate the total value of the VAT exempt items Sakhile (2)
- Demonstrate how the amount indicated by Letter A was calculated. Show all your (3)
- Demonstrate how the amount indicated by Letter B was calculated. Show all your (5) [15]

Solutions | ||
1. | A red T-shirt, ✓ 50% discount. ✓ | (2) |
2. | No, ✓ full refunds are only available for non-sale items. ✓ | (2) |
3. | 2 packs of 6, so 12 eggs. ✓ | (1) |
4. | 2(R5,99) + R6,95 + R11,95 + 2(R7,99) ✓ = R46,86. ✓ | (2) |
5. | VAT incl. items total R151,15. ✓ 14% VAT ✓ of this = R21,16. ✓ | (3) |
6. | Non-VAT items total R46,86. ✓ VAT incl. ✓ + VAT excl. ✓ + R21,16. ✓ VAT = R219,17. ✓ | (5) |
[15] | ||
At some clothing and food stores, it is possible to open an account, buy goods on credit and pay off what you owe the store on a monthly basis.
Worked example 2
Bulelwa has an Edgars store account. She receives the account statement shown above.
- At which six stores can Bulelwa use her store card?
-
- How much must she pay on her account?
- When is this amount due?
- Will she be charged extra if she pays the due amount late? If so, how much?
- How much did Bulelwa pay into her account on 25/04/2012?
-
- How much credit does she still have available?
- What is the difference between “credit available” and “credit limit”?
- How much is the balance brought forward from the previous statement?
- How much did Bulelwa spend at Edgars in the month of April 2012?
- The closing balance on this statement includes 14% VAT. Calculate the VAT included in the closing balance of R742,37.
Solutions
- Edgars, Boardmans, Prato, Temptations, CNA and Red Square.
-
- R240,00.
- 01/06/2012.
- Yes. A charge of 22,10% per annum is added to late payments.
- She paid R240,00 into her account.
-
- Bulelwa has R3 307,00 credit on her account.
- Credit available is how much credit Bulelwa has left. Credit limit is how much credit is allowed in total, at any one time (i.e. she can buy items totaling R4 049 on credit).
- R692,42.
- R99,95 + R190,00 = R289,95.
- The closing balance is 114% of the balance before VAT was added. The VAT is 14% of this final amount.
So, VAT = R742,37 ÷ 114% × 14%
= R742,37 × 14 /114
= R91,17.
Activity 2: Reading an account statement
|
Jet Stores | |
Edgars Stores | |
CBS stores | |
Ms D T Bears 222 Straight Str Hababa City 1313 | Credit available: R1 550,35 | |||||
Date: 02/06/2011 | ||||||
Statement | Instalment R280.00 | |||||
Date | Ref. no. | Details | Amount | Balance | Total Due R280.00 | |
22/05/11 | Opening balance | 3 450.15 | Due Date | |||
22/05/11 | Cash payment Thank you! | 280.00 | 3 170.15 | Credit limit | ||
23/05/11 | 12 months plan Purchase Jet Menlyn | 55.50 | 3 225.65 | Enquiries | ||
Purchase Jet Menlyn | 120.15 | 3 345.80 | Office Hours | |||
Purchase Jet Menlyn | 500.00 | (a) | ||||
Closing balance | (b) | |||||
Study the account statement above and answer the following questions.
- What is Daisy’s opening balance? (1)
- How much is her credit limit? (1)
- Why is there a due date on the statement? (2)
- Calculate the value of the goods she purchased this month. (2)
- Calculate the values (a) and (b). (2)
- The company charges 33% per annum on late payments. How much will Daisy owe if she does not pay the R280,00 installment until 07/07/2011? (6)
- The closing balance includes VAT. Calculate the original total, excluding VAT. (2)
- Why is the “Credit Available” amount not the same as the “Credit Limit”? (2) [18]
| Solutions | |||
| 1. | R3 450,15. ✓ | (1) | |
| 2. | R5 600,50. ✓ | (1) | |
| 3. | To regulate payment and also add charges if the account is not paid by that date. | (2) | |
4. | Purchases = R55,50 + R120,15 + R500,00 ✓ = R675,65. ✓ | (2) | |
5. | (a) R3 845,80. ✓ (b) R3 845,80. ✓ | (2) | |
6. | (33/100 × R280,00) ÷ 12 = R7,70. ✓✓ | ||
She will owe R3 845,80 ✓ – R280 ✓ + R7,70 ✓ | (6) | ||
= R3 573,50. ✓ | |||
7. VAT (excl.) Price = R3 845,80 ✓ ÷ 1,14 = R3 373,51. ✓ | (2) | ||
8. It shows that she still owes the company ✓, although they gave power of R5 600,50. ✓ | her buying | (2) | |
[18] | |||
Municipal bills
A household must pay municipal charges for rates, water and electricity.
Worked example 3
Look at the municipal bill given on the previous page.
- Mrs Gwayi received the above municipal invoice for electricity and refuse.
- At which four stores or outlets can she pay for electricity and refuse?
- If Mrs Gwayi wants to query this bill, what number should she phone?
-
- According to the bill, when did Mrs Gwayi last make a payment to the municipality?
- How much was her last payment?
- If Mrs Gwayi receives the invoice on 10 September 2013:
- What is the minimum amount that she needs to pay immediately?
- What additional amount must she pay before 19 September?
- If Mrs Gwayi wants to pay her invoice in full, what is the total amount she owes?
- The total amount due (‘total liability’) includes 14% VAT but that percentage is not listed separately on this invoice. Calculate the VAT included in the total amount. Round off your answer to 2 decimal places.
Solutions
-
- She can pay at Absa, Checkers, Shoprite and the Post Office.
- 086 010 3089
-
- 29/07/2013
- R349,63
-
- R1 683,00
- R393,72
- R2 076,72
- Total amount = R2 076,72 VAT = 2 076,72 × 14 ÷ 114
= R255,04
Study the Eskom bill below and answer the questions that follow.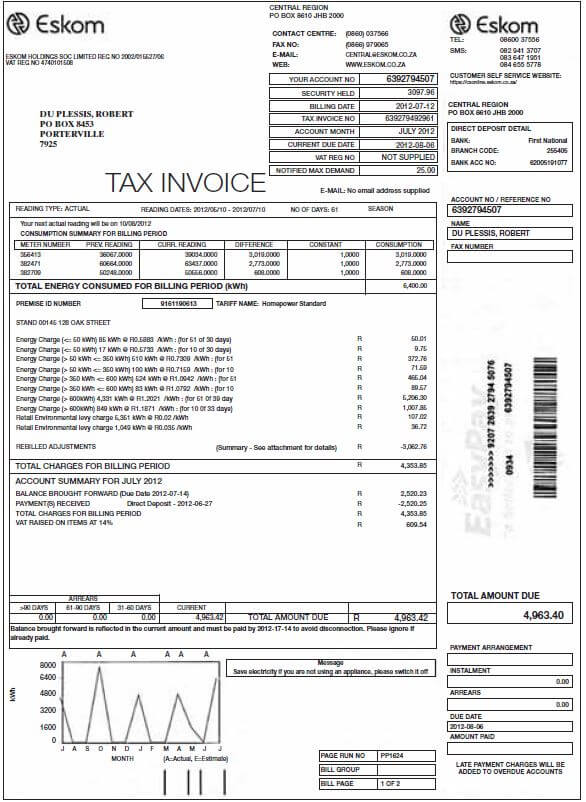
Mr du Plessis gets the account for his electricity consumption over 2 months (see above bill). He has three electricity meters on his property for two small houses and a flat on the premises and they are billed together.
-
- What is the total amount due? (1)
- What does “billing period” mean and how long is it in this case? (4)
- When did Mr du Plessis last pay his electricity account and how much did he pay? (2)
- Why is the amount for “Payment(s) Received” negative (–R2 520,25)? (3)
- What do you think “Balance brought forward” means? (3)
- The consumption levels for the first two meters listed (meter numbers 356413 and 382471) are fairly similar, both close to 3 000 kWh. The consumption level for the third meter (number 382709) is much lower.
- Why do you think this might be so? (2)
- Give examples of factors that might increase a household’s electricity consumption. (2)
- The graph in the bottom left corner of the invoice shows the meter readings for Mr du Plessis’ electricity consumption over the previous 12 months.
- What do you think the letters under the horizontal axis mean?
Is there anything unusual about their order? (2) - What does the spiky shape of the graph indicate? Give a possible reason for why the consumption (in kWh) is high for some months and at zero for others. (3)
- Can you see a pattern between the high points (spikes) on the graph and the number of months that has passed? What does this pattern suggest about how often Mr du Plessis’ metre is read? (3) [25]
- What do you think the letters under the horizontal axis mean?
Solutions
-
- R4 963,42 ✓
- The billing period is a specific number of days ✓ covered by the invoice. The standard billing period is one month. ✓ In this case it is 61 days ✓, so this invoice includes electricity consumption for the 61 days before the billing date. ✓ (4)
- His last payment was on 2012-06-27, for R2 520,25. ✓✓ (2)
- The amount is negative to indicate that R2 520,25 ✓ was subtracted from what Mr du Plessis owed. (This payment is called a credit ✓ – it is money being paid into the account). ✓ (3)
“Balance brought forward” is the amount of money from the previous ✓ invoice that must be paid, or is still outstanding. In this invoice, the amount still outstanding was due to be paid by 2012-07-14 ✓, and Mr du Plessis paid it in full on 2012-06-27. ✓ (3)
- If the third meter is for the small flat on the property, for example, then the consumption will be lower ✓ because there will be fewer ✓ lights and plugs.(2)
- One major factor that affects how much electricity people use is the weather. In winter, ✓ for example, people use more ✓ lighting (because it gets dark ✓ earlier), heaters, electrical blankets, and appliances like tumble driers. (any 2) (2)
-
- The letters under the graph stand for the months of the year. They are not in the usual order (J (January), F (February), M, A, etc.) ✓ but are arranged in the order of the last months starting 12 months ago and ending with the most recent month (J (July), A (August) ✓, S (September) to J (June)).
- The large spikes indicate when the meter reading for consumption was high ✓, and the flat segments of the graph indicate that it was at 0kWh ✓. It is unlikely that Mr du Plessis used no electricity in the months when the meter reading was zero – it is more likely that the meter was not read at
all (for example, if no one was home when the meter reader arrived) in those ✓ months, and so consumption was entered into the system as being 0kWh. (3) - Initially, the peaks in the graph occur once every three months ✓ (July, October, January, April). Then the graph changes and there are non-zero readings for April and May ✓, no reading for June and again a reading for July ✓. So, from July 2011 to April 2012, the meter was read once every 3 months. Then it was read for 2 consecutive months (April and May), and then again two months later. (3) [25]
Many different cell phone packages are available for pre-paid or contract accounts. You need to decide on your own needs, and then work out which account would be best for you.
Study the mobile phone invoice on the previous page.
- What is Mr. Finlay’s cell phone number?
- What kind of cell phone do you think Mr. Finlay owns? Explain your answer.
- For which service did he receive a 100% refund? Explain your answer.
- Does Mr. Finlay receive any other discounts? If so, what were they?
- What is the most expensive item in the list of transactions? What do you think this amount is for?
- How do we know that Mr. Finlay has been an MTN client since at least November 2011?
- Can Mr. Finlay make calls to international numbers on his phone? Explain your answer.
- How many days does he have to query this invoice?
- MTN includes the average spent per month, over the last 6 months. Show how they calculate this average.
- Show how MTN calculated the 14% VAT that is added to the total excluding VAT.
Solutions
- 081 423 7012
- The transaction column lists his phone as a Blackberry.
- The Blackberry Internet service (added and then subtracted)
- Mr. Finlay received a R7,02 discount for “CLI Monthly Discount”.
- The most expensive item is “MTN 200 TopUp Subscription”. This is the fixed amount that Mr. Finlay pays for his cell phone contract (an MTN TopUp 200 type contract) each month.
- The invoice includes Mr. Finlay’s last 6 billing periods, the first of which is dated 11-2011.
- Yes. One of the “Additional Services” listed in the grey column on the left hand side of the page is “Allow International Dialling”.
- Mr. Finlay has 30 days to query the invoice.
- Average = Total amount over 6 months ÷ number of amounts
= (398 + 299 + 299 + 299 + 299 + 299) ÷ 6
= 1 893 ÷ 6 = R315,50 - Total excluding VAT = R262,28
14% of R262,28 = R262,28 × 14 ÷ 100 = R36,72

Oliver receives the cell phone bill on the previous page.
- What is the balance brought forward from the previous invoice? (1)
- On what date was the payment of this balance made? (1)
- When is the payment for the current outstanding amount due? (1)
- What subscription service does Oliver get for free? (1)
- What subscription does Oliver get a full refund for? (1)
- What is the billing period for this invoice? (1)
- Oliver wants to query the last payment he made. List four things he could use as a reference number. (4)
- Oliver wants to check that the VAT calculated on the total amount due is correct. Show how he can do this. Show all your calculations. (3) [13]
Solutions | |
1. R99,00 ✓ | (1) |
2. 02/07/2012 ✓ | (1) |
3. 31/07/2012 ✓ | (1) |
4. HSDPA Voice Tariff ✓ | (1) |
5. VAS Balance Notification✓ | (1) |
6. The month of July 2012✓ | (1) |
7. His cell phone number ✓, his account number ✓, the invoice number ✓ and the payment ✓ reference number. | (4) |
8. Total without VAT = R86,84. ✓ 14% of this = R86,84 ✓ ´ 14 ÷ 100 = R12,157 ≈ R12,16 ✓ | (3) |
| [13] |
3.2 Budgets, income and expenditure statements
A budget is a plan for using income to cover expenses.
Table of some Income and Expenses
INCOME | EXPENSES |
|
|
Types of Income or Expenses:
- Fixed means it does not change with
- Variable means it changes over time, according to the
- Occasional means it occurs from time to
There are several things you should aim for in your personal budget:
- It should list all of the items that are needed and should try to anticipate unforeseen
- It should be realistic, so that you can stick to
- It should focus on the high priority items (essential items such as food and health care). If too much of the income is spent on non- essential items and not on savings, your budget is going to become problematic in the future.
- An ideal budget should include a plan to save money for the future, or to pay off debts to allow for savings in the following
- It should be balanced. If your income is less than your expenses, then you need to revise it until the two sides If your income is more than your expenses, then you should plan to save the extra money.
Worked example 5
Douglas wants to travel from Cape Town to Durban to visit his cousin. His parents said that they can give him R500 towards the trip. He decides to draw up a budget to determine how much money the trip will cost. His uncle has offered to give him a lift home so he only needs to budget for the trip to Durban. He has R2 000 saved in his bank account. He wants to have some spending money left over when he gets there.
He phones Rainbow Buses to find out how much it costs to travel from Cape Town to Durban. They give him two options:
- OPTION 1: Leave Saturday morning and travel straight to Durban. The trip costs R1 200 and he will need to pay for 3 meals at R30 per meal.
- OPTION 2: Leave Saturday morning and travel to Plettenberg Bay first. The trip costs only R400. He can then catch a bus on Sunday morning to Durban. This bus trip will cost R500. If he does this he needs to find a place to stay on Saturday night and budget for three extra meals (estimated at R30 each). He estimates that a Backpackers’ Lodge would be the cheapest place to stay, at R200 a night.
Income | Expenses | Running total of money that he has | |
Money from parents | |||
Savings | |||
Bus fare | |||
Meals on bus | |||
Accommodation |
- Copy the above budget sheet and fill in the amounts for income and expenses in the correct columns for Option 1 and Option 2
- Would you advise Douglas to take Option 1 or Option 2? Explain your answer.
Solutions
- OPTION 1
OPTION 2Income
Expenses
Running total
Money from parents
500
500
Savings
2 000
2 500
Bus fare
1 200
1 300
Meals on bus
3 ´ 30 = 90
1 210
Accommodation
0
1 210
Income
Expenses
Running total
Money from parents
500
500
Savings
2 000
2 500
Bus fare
400 + 500 = 900
1 600
Meals on bus
6 ´ 30 = 180
1 420
Accommodation
200
1 220
- Although the bus fare for Option 2 was cheaper the costs are quite similar in the end.
Option 1 is much more convenient and is quicker, so he should choose this option.
Consider the previous activity, where Douglas planned to travel to Durban. He eventually decided to travel to Durban using bus Option 1. He kept all the receipts and till slips so that he could write a statement to see how much money he actually spent. Read the summary below of Douglas’s bus trip.
When Douglas arrives at the bus station to buy the ticket, he finds that the advertised price does not include VAT, and he needs to add 14% to the cost. To add to his problems, the bus breaks down and Douglas needs to find a place to stay the night in Knysna. He finds a backpackers’ lodge that costs R200 a night for a shared room. He also needs to rent a locker for R20 to keep his luggage safe. Apart from three meals on the bus, he needs to buy an extra supper and breakfast, which cost him R30 each.
- Fill in a table like the one used for his budget, to show his actual expenses and the running total of expenses.
Expense description
Amount
Running total of expenses
- What is the amount of money he ends up with as spending money in Durban?
Remember: he had R2 500 to begin with.
Solutions
-
Expense description
Amount
Running total of expenses
Bus Fare
R1 200 + R168 VAT
R1 368
Meals on Bus
R90
R1 458
Backpacker’s accommodation
R200
R1 658
Locker
R20
R1 678
Meals
R30 × 2 = R60
R1 738
- He has saved R2 000 and received R500 from his parents.
R2 500 - R1 738 = R762 to spend in Durban
Worked example 6
A household has the following monthly expenses:
- rent R2 300
- transport R520
- cell phone R200
- pre-paid electricity R800
- water bill R350
- TV contract R250
- loan repayment R310
- furniture store account R570
- clothing store account R315
- groceries R2 500
- medical expenses R75
They live on the following monthly income: a state pension of R1 140, a disability grant of R1 140 and a salary of R5 250. This month, one of the children falls ill and they have additional medical expenses of R500 for doctor’s visits and medication.
- Draw up an income and expense statement for the household for this month.
- What is the total difference between the income and expenses?
- Which costs could be reduced in their budget?
- If those costs were reduced, would the family have enough money to cover their expenses?
Solutions
-
Income
Expenses
State Pension
1 140
Disability grant
1 140
Salary
5 250
Rent
2 300
Transport
520
Cell phone
200
Pre-paid electricity
800
Water bill
350
TV contract
250
Loan repayment
310
Furniture store account
570
Clothing store account
315
Groceries
2 500
Medical expenses
75 + 500 = 575
Total
7 530
8 690
- R8 690 - R7 530 = R1 160 more for expenses than they receive in
- Water and electricity usage could be reduced, the furniture and store accounts could be paid off and closed, and grocery expenses could be
- They aren’t thousands of rands over budget so a series of small reductions across their expenses would bring their expenses in line with their income.
Look at the family budget for the month of December 2013, for the Philander family. There are two adults and two school children in the family.
Item | Expenditure | Expenditure | Income |
Fixed | Variable | ||
Mrs Philander’s salary | R9 500 | ||
Mr Philander’s salary | 1. | ||
Additional income | 2. | ||
Bond repayment | 3. | ||
Food | 4. | ||
Edgars clothing account | 5. | ||
School fees | 6. | ||
Transport | 7. | ||
Entertainment | 8. | ||
Savings | 9. | ||
Car repayment | R1 300 | ||
Municipality rates | 10. | ||
Electricity | R200 | 11. | |
Vodacom contract cost | R700 | ||
Total | ? | ? | ? |
Surplus or deficit? |
Complete the above family budget by using the following information.
- Mr Philander’s income: He works 20 days per month at a rate of R500 per (1)
- Additional income: Mr Philander owns additional property which he rents out to people at a fixed charge of R2 500 per (1)
- The monthly bond repayments are fixed at R5 550 per (1)
- The average amount spent on food each month comes to R2 500. Mrs Philander believes that this should be increased by 10% due to recent food price (1)
- Mr Philander pays Edgars an amount of R800 per month. However, since he bought his children their school uniforms on account, he estimates that this amount will increase by a further 12%. (1)
- The school fees are R1 200 per child per (1)
- Transport costs are as follows: For the children, taxi fare per child = R5,00 per trip to school and another R5,00 each for the trip home. There are 20 school days in a month. Mr Philander first drives his wife to work and then goes to work himself. In the evenings he picks her up and they drive home again. They both work 20 days per month. Mr Philander has noticed that his car uses an average of 4 litres of petrol per day each time he does this.
On the other 10 days of the month, his car uses an average of 3 litres per day. The cost of petrol is R10,50 per litre. Calculate the total amount that should be budgeted for transport. (5) - The amount budgeted for entertainment is estimated at 5% of the combined income of Mr and Mrs (2)
- Savings are currently 5% of Mrs Philander’s (2)
- The amount budgeted for municipal rates is 5% of the total income earned by the Philander (5)
- The fixed component of the electricity account is currently R200 per month. The variable component is calculated as follows: the average amount of electricity consumed by the Philander household is 550 kilowatt hours per month at a rate of R0,50 per kilowatt hour. (4)
- Is the Philander family within budget? Explain your (5) [29]
Solutions
- 20 ´ R500 = R10 000 ✓
- R2 500 ✓
- R5 500 ✓
- R2 500 + R250 = R2 750 ✓
- R800 + R96 = R896 ✓
- R1 200 ´ 2 = R2 400 ✓
- Taxi fare: R10 per day ´ 2 children ´ 20 days ✓ =R400. ✓
Petrol: (20 × 4 litres ×R10,50) ✓ + (10 × 3 litres × R10,50) ✓ = R1 555 ✓ - Total salaries = R19 ✓ 5% of this is R975. ✓
- 5% of R9 500 ✓ = R475. ✓
- Total income = salaries ✓ + additional income ✓ = R19 500 + R2 500 ✓
= R22 000. ✓ 5% of this is R1 100. ✓ - 550 × R 0,50 ✓ = R275; ✓ monthly is R275 ✓ + R200 = R475. ✓
- The total for fixed expenses is R12 621 ✓. The total for variable expenses is R5 755 ✓. So, the total for all expenses is R18 376. The total income for the household is R22 000, so yes – they are within budget ✓, because their income is greater than their total ✓ expenditure and they have a surplus of money. ✓
Banks offer different types of accounts and services.
- Savings account: A bank account that earns You can use a savings account for short – term savings.
- Cheque or current account: A bank account that is used to deposit and withdraw money by visiting the bank branch, using an ATM or Internet banking or by writing a These are usually available to people who earn a regular income.
- Fixed deposit account: This account is aimed at those who have a lump sum they want to invest over a fixed period of time (i.e. a medium or long term saving). Interest is also earned on the investment.
- Credit account (with credit card): An account either with a store or bank, that allows the account holder to purchase items now and pay for them Debit account (with debit card): Debit cards can be used to pay for purchases. When it’s swiped, money is deducted from the account.
A bank statement is usually sent to the account holder monthly. Bank statements show the following for each transaction:
- the date of the transaction
- a description of the transaction, showing the type of transaction
- the amount of the transaction, indicating whether it is a debit or credit (often in different columns)
- a column for the balance after each
Account holder: The person whose name the account is in.
Opening and closing balance: The amount of money in the account at the beginning and the end of the period.
Transaction: Any event where money moves into or out of an account.
Debit transaction: Amount of money paid out of an account.
Credit transaction: Amount of money deposited into an account.
Worked example 7
Xola receives the following statement from her bank, detailing her transactions from 25/01/2013 to 20/02/2013. Study the statement and answer the questions that follow.
Date | Description | Amount | Amount | Balance |
25/01/2013 | Salary | 8 000,00 | 8 050,50 | |
27/01/2013 | Car insurance | -100,00 | 7 950,50 | |
01/02/2013 | Electronic transfer Mr. Serei (RENT) | -3 000,00 | 4 950,50 | |
01/02/2013 | Debit order Healthsaver medical aid | -500,00 | 4 450,50 | |
02/02/2013 | Debit order Mobi contract | -250,00 | 4 200,50 | |
03/02/2013 | Debit order Supa Fashion Store | -300,00 | 3 900,50 | |
05/02/2013 | Purchase at Shop ‘n Save | -2 000,00 | 1 900,50 | |
14/02/2013 | PAYMENT Mrs. S Khumalo | 500,00 | 2 400,50 | |
20/02/2013 | Automechanix | -1 000,00 | 1 400,50 | |
Total remaining: | 1 400,50 | |||
- How can you tell the difference between the debits and the credits in this statement?
- List Xola’s debits and credits for the month
- In the first line of this statement, Xola receives a salary of R 8 Look at the balance and work out what she had in the account before the payment was made.
- Xola receives some birthday money as well as her salary this Identify and write down the birthday transaction.
- How much money would she have been left with on 20/02/2013, if she hadn’t received money for her birthday?
- Xola wants to save 15% of her remaining money this How much can she save?
Solutions
- The credits are positive values and are in the left-hand column, while the debits are negative and are in the right-hand column.
- Credits: Salary, deposit from Mrs S Debits: car insurance, rent, medical aid, cell phone contract, clothing store account, groceries, car repair.
- R 8 050,50 - R 8 000 = R 50,50, so she had R 50,50 in her account before her salary was paid.
- 14/02/2103 PAYMENT Mrs S Khumalo R500.
- R 1 400,50 – R 500 = R 900,50.
- 15% of R 1400,50 = 1400,50 × 0,15 = R 210,08.
Below is an incomplete bank statement for Koketso’s savings account at the end of March.
Date | Transaction | Payment | Deposit | Balance |
27/02/2013 | OPENING BALANCE | 2 304,85 | ||
01/03/2013 | INTEREST ON CREDIT BALANCE | 13,95 | ||
01/03/2013 | CHEQUE (SALARY) | 2 100,00 | ||
01/03/2013 | ATM CASH | 400,00 | ||
05/03/2013 | ATM CASH | 800,00 | ||
10/03/2013 | ATM DEPOSIT | 600,00 | ||
22/03/2013 | SPENDLESS DEBIT CARD PURCHASE | 235,95 |
- How can you tell the difference between the debits and the credits in this statement? (2)
- Copy Koketso’s statement and complete the balance column asa running total. (6)
- What is Koketso’s balance on the 22nd of March? (1)
- Koketso aims to keep a minimum balance of R2 500 in his account to earn interest. Is he succeeding? (1) [10]
Solutions
- As payments (debits) ✓ and deposits (credits) ✓ respectively.
-
Date
Transaction
Payment
Deposit
Balance
27/02/2013
OPENING BAL
2 304,85
1/03/2013
INTEREST ON CREDIT BALANCE
13,95
2 318,80
1/03/2013
CHEQUE (SALARY)
2 100,00
4 418,80
1/03/2013
ATM CASH
400,00
4 018,80
5/03/2013
ATM CASH
800,00
3 218,80
10/03/2013
ATM DEPOSIT
600,00
3 818,80
22/3/2013
SPENDLESS DEBIT CARD PURCHASE
235,95
3 582,85
- R3 582,85 ✓
- He has succeeded since the beginning of March. ✓
Banks charge fees for the services they provide.
Worked example 8
Arthur’s bank, Egoli Bank lists the following banking fees.
Arthur subscribes to self-service banking and pays a monthly maintenance fee. In the space of a month Arthur performs the following transactions:
- He deposits R335,00 in cash at an Egoli Bank ATM.
- He withdraws R500 cash at another bank’s ATM
- He withdraws R100 cash over the counter at an Egoli Bank branch
- He enquires twice about his balance, over the counter at an Egoli branch.
- He draws cash, whilst buying groceries at a till point at his local supermarket
- He makes 3 electronic account payments to pay his rent, electricity and phone bill
| TRANSACTION | FEE |
| MONTHLY FEES | |
| Monthly maintenance fee | R5,00 |
| Self-service banking subscription fee | R15,00 |
| Deposits | |
| Cash (over the counter/at Egoli Bank ATM) | R5,00 |
| Cheque (over the counter/at Egoli Bank ATM) | Free |
| CASH WITHDRAWALS | |
| Over the counter | R10,00 |
| Egoli Bank ATM | R5,00 |
| Another bank’s ATM | R7,00 |
| Tillpoint - cash only | R1,00 |
| Tillpoint - cash with purchase | R2,00 |
| ACCOUNT PAYMENT AND PURCHASES | |
| Electronic transfers between accounts | Free |
| Electronic account payment | Free |
| Stop order | R5,00 |
| Debit order - internal | R2,50 |
| Debit order - external | R5,00 |
| BALANCDE ENQUIRIES | |
| Over the counter | First free per month,then R10,00 |
| Egoli Bank ATM | First free per month,then R1,00 |
| Another bank’s ATM | R2,00 |
| Self-service banking | Free |
- Calculate the total bank charges for these transactions
- Arthur has a balance of R650 in his bank account at the end of the month
- Calculate the ratio of the total bank fees to the month end balance
- Express this ratio as percentage. (Round off your answer to 1 decimal place )
- Suggest ways in which Arthur could reduce his banking fees
Solutions
- R5,00 (Monthly maintenance fee) + R15,00 (self-service banking) + R5,00 (cash deposit at Egoli bank) + R7,00 (cash withdrawal at other bank) + R10,00 (cash withdrawal over the counter) + R0,00 (first balance enquiry) + R10,00 (second balance enquiry) + R2,00 (till point cash withdrawal) + ( 3 × R0,00) (free electronic account payments) = R54,00.
- (a) Banking fees: closing balance = 54 : 650 or 27 : 325
(b) 54 ÷ 650 × 100 = 8,3% or 27 ÷ 325 × 100 = 8,3% - Arthur could withdraw cash at Egoli Bank ATM’s only, not at other banks’ ATM or over the counter at a bank branch. He could ask for a balance enquiry from an Egoli ATM, or via self-service banking, instead of over the counter. He could withdraw cash only at a till point, without purchasing anything.
Activity 8: Calculating banking fees
Mia has recently opened a Global account at Capital Bank. She is concerned about her monthly bank charges. Use the provided brochure and list of her account activities for the month of April to answer the questions below.
Date | Activities | Amounts |
01 April 2013 | Balance of previous month carried forward | R210,25 |
01 April 2013 | Old Mutual Policy x74534: Debit order returned: insufficient funds* | R254,39 |
01 April 2013 | Balance enquiry (mobile) | R0,00 |
02 April 2013 | Davidsons Textiles: Salary deposit* | R450,00 |
02 April 2013 | Shoprite Purchases: debit card* | R847,21 |
02 April 2013 | Shoprite: Cash withdrawal* | R250,00 |
07 April 2013 | Old Mutual Policy x74534: Branch Payment | R254,39 |
15 April 2013 | Edgars: Purchases: Debit card* | R149,59 |
20 April 2013 | Capital Bank ATM Withdrawal: * | R200,00 |
23 April 2013 | Shoprite: municipal account payment* | R639,00 |
28 April 2013 | FNB ATM withdrawal* | R500,00 |
29 April 2013 | Balance statement at the branch | R3,00 |
30 April 2013 | Monthly admission fee | R4,50 |

*denotes SMS notification for April
- How many withdrawals did Mia make during this month? (1)
- Calculate the amount of money that was spent on monthly shopping (1)
- Use the relevant resources to calculate the amount of bank fees that Mia will pay for April. (9)
- Suggest how Mia can further reduce her banking (3) [14]
Solutions
- Three. ✓ (1)
- R847,21 + R149,59 = R996,80 ✓ (1)
- Returned debit order R4,00 ✓. Cash withdrawal at Shoprite: R1,00 ✓. Old Mutual debit order payment at branch: R3,00 ✓. Capital Bank ATM withdrawal: R4,00 ✓. FNB ATM withdrawal: R7,00 ✓. Balance statement in branch: R3,00 ✓. Monthly admin fee: R4,50 ✓. 8 SMS notifications: R3,20 ✓. Total: R29,70 ✓. (9)
- She could do away with SMS notifications ✓, only draw cash at till points ✓ and make sure that her debit (3) orders ✓ don’t get returned. [14]
- Interest rate: A percentage charged for the borrowing, or loan, of a sum of money over a given period of time.
- Interest: The amount of money that you are charged (by the lender of money, e.g. the bank) for borrowing an amount of money, over a period of time.
Simple interest is calculated on the original amount, and is the same each time it is paid.
Calculating interest amounts and interest rates
If we know what the interest rate is, we can calculate the interest value quite simply.
- For example, 10% interest on R3 500 = R3 500 × 10% = R350. So the interest amount is R350 and the total amount is R3 500 + R350 = R3 850.
If you are given the final amount, then you follow these steps to find the interest rate:
- Find the difference between the final amount and the original amount: this gives you the amount of interest.
- Work out what percentage the amount of interest is of the original value, or of the amount owed (in hire purchase).
Worked example 9
You see an advert for a wall unit. The cash price of the wall unit is R6 499,99. Alternatively, you could choose to buy it on hire purchase and pay for it in instalments over 3 years. If you choose to pay it off in instalments, you will pay interest every month on the wall unit.
- Calculate what the wall unit will cost if you pay a cash deposit of R650, and 36 monthly instalments of R449 each. (The total = cash deposit + 36 monthly instalments.)
- Calculate how much interest you will pay in total (in Rands) if you pay off the wall unit in instalments. (Hint: Interest amount = total payments – cash price.)
- Calculate the interest rate. (Interest rate = (Interest ÷ money owed) × 100).
- Do you think it is better to save up and buy the wall unit at the cash price, or pay it off over 3 years? Explain your answer.
Solutions
- Total = cash deposit + 36 monthly instalments = R650 + (R449 × 36 months) = R16 814.
- Interest = total payments – cash price = R16 814 – R6 499,99 = R10 314,01.
- You owe R6 499,99 – R650 = R5 849,99. Interest rate = (R10 314, 01 ÷ R5 849,99) × 100 = 176,3% over 3 years which is 58,8% per annum.
- It is much cheaper to save up and buy the wall unit at the cash price. Over three years, the total amount you would pay in instalments is almost three times the cash price.
You found the following advertisement in a local newspaper. Answer the questions below.
- Does the advertisement indicate the percentage of interest that will be charged if the TV is not paid for in cash? (1)
- What will the balance be once the deposit has been paid? (4)
- Will the interest be charged on the full purchase price or on the balance? (1)
- How much will the instalment be per month? (1)
- How much will you have to pay for the TV in total? Use the formula:
Total to be paid = Deposit + (Instalment x number of instalments) (6) - How much interest (in Rands) will you have paid once you have completed paying off the TV? Use the formula:
Interest = Total paid – cash price. (3) - What simple interest rate per annum will you be paying on the outstanding balance? (4) [20]
REMEMBER:
- You calculate the interest rate on the money that you owe after you pay the deposit.
Solutions
- No. ✓
- Balance = Cash price ✓ – Deposit ✓ = R15 600 - R1 560 ✓ = R14 040. ✓
- It will be charged on the account balance. ✓
- R356,24. ✓
- Total Payable = Deposit + (Instalment amount ´ number of instalments)
= R1 560 ✓ + [R356,24 ✓ × (12 × 5)] ✓ = R1 560 ✓ + R21 374,40 ✓
= R22 934,40. ✓ - Interest = total paid – cash price
= R22 934,40 ✓ - R15 600 ✓ = R7 334,40 ✓ - R7 334,40 ✓ ÷ R14 040 ✓ × 100% = 52,24% ✓ over 5 years, which is 10,45% ✓ p.a.
- Compound interest is calculated on the current balance.
- It yields more interest over time than simple interest.
Worked example 10
Mr. Moloke has two options for borrowing money.
- His uncle has offered to lend him R16 000 for five years at 18% per annum, simple interest
- His personal bank will lend him R16 000 for five years at 16% interest compounded per annum
Determine the cost of the two options to recommend which one would be best for Mr. Moloke.
Solutions
- Simple interest = R16 000 × 18 ÷ 100 × 5 = R14 400
Total amount = R14 400 + R16 000 = R30 400 - Compound interest
First year = R16 000 × 16 ÷ 100 = R2 560
Total = R2 560 + R16 000 = R18 560
Second year = R18 560 × 16 ÷ 100 = R2 969,60
Total = R2 969,60 + R18 560 = R21 529,60
Third year = R21 529,60 × 16 ÷ 100 = R3 444,74
Total = R3 444,74 + R21 529,60 = R24 974,34
Fourth year = R24 974,34 × 16 ÷ 100 = R3 995,89
Total = R3 995,89 + R24 974,34 = R28 970,23
Fifth year = R28 970,23 × 16 ÷ 100 = R4 635,24
Total = R4 635,24 + R28 970,23 = R33 605,47
Therefore the personal loan is cheaper.
People borrow money when they need it most and they have to pay interest on the borrowed amount.
Worked example 11
The table below is an extract from a letter from Sanlam to Mr. Moloke. It shows the amounts that are available on instant loan from Sanlam and the repayment involved.
Dear Mr. Moloke
As a valued customer, we are pleased to be able to offer you a personal loan at the following rates.
Loan amount | 24 months | 36 months | 48 months | 60 months |
R4 000 | R229 | R174 | R147 | R131 |
R8 000 | R448 | R338 | R285 | R253 |
R16 000 | R864 | R643 | R534 | R470 |
R25 000 | R1 344 | R1 000 | R830 | R730 |
These loan repayments include a monthly premium of R3,95 per R1 000 of the loan and a monthly administration fee of R9,50 for your optional personal protection plan.
Answer the following questions.
If Mr. Moloke chooses to borrow R16 000 from Sanlam, calculate how much he will finally repay if he takes the loan over:
- 24 months
- 60
Do you advise him to borrow for a longer or shorter time?
Solutions
- 24 × R864 = R20 736
- 60 × R470 = R28 200
Borrowing for a short time involves less interest.
Mosima wants to buy an LCD TV and saw it advertised at R25 000. She does not have enough money to pay cash for the TV, so she has the option of either taking a loan from a microlender or paying by means of an instalment sale (hire purchase) agreement.
Suppose Mosima borrows R25 000 from a microlender to pay for the TV. The amount she has to repay every month depends on the length of time she takes to repay the loan. The table below shows the different options she can choose from.
Number of monthly instalments | |||||
12 | 18 | 24 | 36 | 42 | |
Loan amount | R25 000 | R25 000 | R25 000 | R25 000 | R25 000 |
Initiation Fee | R1 140 | R1 140 | R1 140 | R1 140 | R1 140 |
Monthly Admin. Fee | R57 | R57 | R57 | R57 | R57 |
Monthly Instalment | R2 283 | R1 875 | R1 562,50 | R1 145,83 | A |
Total Amount paid by the end of loan period | R29 220 | R35 916 | R40 008 | R44 441 | R48 534,06 |
NOTE:
- An initiation fee is the amount charged by the microlender to process the loan application and is payable when the loan has been
- A monthly instalment is the amount paid
- A monthly administration fee is an additional cost that is added to the monthly
- The total amount to be repaid = Initiation fee + [no. of instalments (monthly instalment + admin fee)].
QUESTIONS
- Use the formula to calculate the missing value (2)
- Suppose Mosima chose to repay the loan over 42 months. How much will the loan cost her in total? (1)
- If she buys the TV at R25 000 by means of an instalment sale agreement, she must first pay a 10% deposit, and then pay off the balance owing in equal instalments over 24 months at 33% per annum simple interest. Calculate the amount she has to pay for the (1)
- Calculate the amount she is required to pay for her equal monthly Use the formula:
(balance owing × interest × no. of years) ÷ 24. (2) - Calculate the total cost of the TV if she used this method of payment. (3)
- Mosima decides that she wants to pay for the TV over a period of 24 Why? (1) [10]
Solutions
- R48 534,06 - R1 140 = R47 394,06 over 42 months. ✓
Divide by 42 and subtract R57 to get A = R1 071,43. ✓ - R48 534,06 ✓
- R2 500 ✓
- (R22 500 × 0,33 × 2) ÷ 24 ✓ = R618,75 ✓
- R2 500 ✓ + (24 × R618,75) ✓ = R17 350. ✓
- It costs less in total. ✓
Inflation is the increase of the price of a typical basket of goods and services calculated over a period of time.
Inflation rate is calculated as a percentage.
Worked example 12
- A litre of milk currently costs R9,11. The expected inflation rate for 2015 will be 6,5%. What will the price of the milk be in 2015?
Solution
New price will be = 9,11 + 6,5% × R9,11
= 9,11 + (6,5/100 × 9,11)
= 9,11 + 0,6
= R9,71 - The price of Nike shoes in 2014 is R650,95. What was the price of Nike shoes in 2013, if the inflation rate for 2013 was 6,4%?
Solution
Inflation value = 650,95 × 6,4/106,4 OR Previous price + 6,4% = R650 95
= R39,15 Prev. price + (prev. price × 0,064)
= R650,95
Therefore, Previous price
= R650,95 – R39,15 Prev. price (1+ 0,064) = R650,95
= R611,80 Prev. price = R650,95 ÷ 1,064
= R611,80 - A box of jungle oats increases in price from R17,99 to R19,99. Calculate the inflation rate for this Use the formula:
Inflation rate = current price - previous price × 100%
previous price
Solution
Inflation rate =19,99 - 17,99 × 100%
17,99= 11,1%
- A bar of soap currently costs R8,51 in 2014. The expected inflation rate for 2015 will be 6,3%. What will the price of the soap be in 2015? (2)
- The price of a dress is R1 300,95 in What was the price of the dress in 2013, if the inflation rate for 2013 was 6,5%? (4)
- A set of chairs increases in price from R17 355,75 to R19 943,99. Calculate the inflation rate for this period
Inflation rate = current price - previous price × 100%
previous price (3) - In November 2009 Statistics SA announced that the annual inflation rate was 5,8%.
- Determine the price of a bicycle in November 2008 if it cost R1 586,95 in November 2009. (4)
- Calculate the projected cost of a loaf of bread in November 2014 if it cost R5,45 in November 2008. Assume that the annual inflation rate remained at 5,8% over the given You may use the formula
A = P(1 + i)n (2)
where
A = the projected cost
P = current cost.
i = the annual inflation rate.
n = number of years.
Solutions
- Current cost = R8,51 × 106,3% ✓ = R9,05 ✓ OR
R8,51 ✓ + (R8,51 × 6,3 ÷ 100) = R8,51 + R0,54 = R9,05 ✓ - Inflation Value = R1 300,95 × 6,5 ÷ 106,5 ✓ = R79,40 ✓
Previous price = R1 300,95 ✓ – R79,40
= R1 221,55 ✓
OR
R1 300,95 ✓ ÷ 1,065 ✓✓ = R1 221,55 ✓
3. Inflation rate = (R19 943,99 – R17 355,75) ✓ ÷ R17 355,75 ✓ × 100
= R2 588,24 ÷ R17 355,75 × 100% = 14,91% ✓ - a) Price of bicycle ✓ × 105,8% = R1 586,95 ✓
Price of bicycle = R1 586,95 ✓ ÷ 105,8% = R1 586,95 ÷ 1,058 = R1 499,95 ✓ (4)
b) A = P (1 + i)n
A = 5,45 (1 + 0,058)6 ✓
= R7,64 ✓
3.5 Payslips, deductions and tax
PAYE on a payslip stands for “pay as you earn”. This is the income tax that is deducted directly from your salary every month. PAYE is compulsory for all employees. It is calculated according to a set percentage based on your gross annual income. Tax is collected by the South African Revenue Service (SARS).
UIF stands for “Unemployment Insurance Fund”. It serves as a form of insurance, so that if you lose your job, you may apply for UIF which is a small monthly payout from the government. Employers must pay 2% of each employee’s monthly pay towards UIF. The employees and the employer each contribute 1%.
Depending on your employer, you may be a member of a company pension fund or medical aid.
How is my tax rate calculated, and do I qualify for any rebates?
There are set tax thresholds, which are maximum amounts that you can earn before you are required to pay tax. In South Africa, the highest tax rate is 40%, which applies to individuals earning R638 601 and above per annum. The tax tables themselves are a little more complicated than this, but this will suffice for the purpose of understanding your payslip.
These are adjusted every year and the new tables are announced with the budget. The tax thresholds for individuals for the 2013/14 financial year are:
- individuals younger than 65: R67 111
- individuals aged 65–75: R104 611
- individuals older than 75: R117
Individuals receive standard tax rebates calculated according to age. A tax rebate is an amount of tax by which the total tax due is reduced. In other words, tax rebates reduce the amount of tax you have to pay. The age categories are the same as for tax thresholds, and are known as primary (younger than 65), secondary (65 – 75) and tertiary (older than 75) rebates. They are as follows:
- Primary: R12 080
- Secondary: R6 750
- Tertiary: R2 250
Worked example 13
Use the above payslip, and the information on tax to answer the following questions.
- Calculate the daily earnings of Bloggs.
- (i) How is the amount of UIF calculated?
(ii) How much does the company pay toward UIF? - How is the amount of the PAYE calculated?
Solutions
- Earnings per day = R10 000/ 21,67 = R461,47
- (i) 1% of salary, i.e. 1% of R10 000 = R100
(ii) R100 - In the example above, Joe Bloggs pays R793,33 PAYE per month. Here’s how that figure was calculated:
Joe Bloggs falls into the 18% tax bracket, as he earns less than R165 600 per year.
Gross annual income (R120 000) x tax rate (18%) R21 600
Minus deductions (primary rebate) (R12 080)
Subtotal (total tax due per annum) = R9 520
TOTAL (subtotal divided by 12 months) R793,33
Activity 12: Payslips, deductions and tax
Study the payslip below and answer the questions.
FASHION DIVA | |||
NAME: Lucinda Adams | Payslip nr. 009 | Pay date: 25 August 2013 | |
ADDRESS: 4 Arcade Ave Kriel | BANK DETAILS: ASBA bank Cheque account 19056634486 | ||
INCOME | DEDUCTIONS | ||
Basic salary: | R15 780 | PAYE/TAX | R2 865,83 |
Overtime: | (a) | Medical Aid: | R1 420 |
(38 hrs @ R85 p/h | UIF | (b) | |
(1% of basic salary) | |||
Pension fund ( of the amount paid to medical aid fund) | (c) | ||
Total income: (d) | Total deductions: (e) | ||
Net pay (Income – Deductions): (f) | |||
- Calculate the missing values in order to complete the (6)
- Lucinda sees that R2 865,83 was deducted from her salary for PAYE (also known as personal tax). Use the table and example below to show that the amount was calculated correctly.(8)
INCOME TAX FOR INDIVIDUALS for the tax year 2011/2012
TAXABLE YEARLY INCOME (R)
RATE OF TAX (R)
0 – 160 000
18% of each R1
160 001 – 250 000
28 800 + 25% of taxable income above R160 000
250 001 – 364 000
51 300 + 30% of taxable income above R250 000
364 001 – 484 000
81 100 + 35% of taxable income above R346 000
484 001 – 617 000
128 400 + 38% of taxable income above R484 000
617 001 and above
178 940 + 40% of taxable income above R617 000
TAX REBATES:
Primary rebates – R11 440
Secondary Rebates (persons 65–75 years) – R6 390
Tertiary Rebates (persons 75 years and older) – R2 130TAX THRESHOLD:
Below age 65 years – R63 550
Age above 65 years to below 75 – R99 056
Age above 75 years and older – R110 889EXAMPLE
R556 444 (yearly salary)
R128 400 + 38% of amount above R484 000 (R556 444 – R484 000)
= R128 400 + 38% × R72 444
= R155 928,72 – R11 440
= R144 488,72 (yearly tax)
∴R12 040,73 (monthly tax) - Lucinda wants to buy a coat from Fashion The coat costs R749 including VAT. As she is an employee of the shop, the owner gives her a discount by not charging her VAT (14%) on the coat. Calculate the amount she would have to pay. (2) [16]
Solutions
- a) R3 230 ✓
b) R157,80 ✓
c) R1 065 ✓
d) R19 010 ✓
e) R5 508,63 ✓
f) R13 501,37 ✓ - R19 010 × 12 = R228 120 ✓
Therefore = R28 800 ✓ + (25% × [R228 120 ✓ – R160 000])
= R28 800 + (25% × R68 120)
= R45 830 ✓
Less rebate = R45 830 – R11 440 = R34 390 ✓
R34 390 ÷ 12 ✓
= R2 865,83 ✓ - R749, 00 ÷ 1,14 = R657,02 ✓✓