MAPS, PLANS AND OTHER REPRESENTATIONS OF THE PHYSICAL WORLD GRADE 12 NOTES - MATHEMATICAL LITERACY STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- Scale
- The number scale
- Activity 1: Using the number scale
- The bar scale
- Understanding the advantages and disadvantages of number and bar scales
- Activity 2: Scales and resizing
- Drawing a scaled map when given real (actual) dimensions
- Activity 3: Drawing a scaled plan
- Maps
- Activity 4: Navigating a shopping mall
- Using a road map
- Activity 5: Using a road map
- Elevation Maps
- Plans
- Assembly diagrams and instructions
- Activity 6: Instructions for wiring a plug
- Plans and elevations
- Symbols on a floor plan
- Reading floor plans
- Activity 7: Interpreting a floor plan
- Models
Maps, plans and other representations of the physical world
The two kinds of scale we will be working with in this chapter are the number scale and the bar scale.
- is expressed as a ratio like 1 : 50.
This says that 1 unit on the map represents 50 units on the ground. For example, 1 cm on the map will represent 50 cm on the ground and 1 m on the map will represent 50 m on the ground.
To use the number scale, you need to measure a distance on a map using your ruler or use the distance provided, and then multiply that measurement by the “real” part of the scale ratio given on the map, in order to get the real distance.
e.g. Worked example 1
- You measure the distance between two buildings on a map to be 10 If the map has a number scale of 1: 40, what is the actual distance in metres on the ground?
- You are given a map with the number scale 1: 50 000. You measure a distance of 15 cm on the What is the actual distance in km?
Solutions
- Scale is 1:
10 cm × 40 = 400 cm = 4 m
The distance on the ground (in real life) is 4 m. - Scale is 1 : 50000
Therefore actual distance is 15 cm × 50 000 = 750 000 cm = 7,5 km.
Activity 1: Using the number scale
Study the school map given below and answer the questions that follow.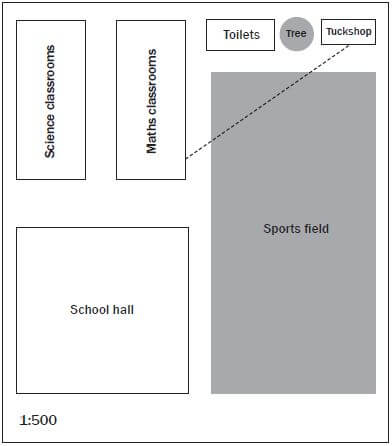
- Use the given scale to calculate the following real dimensions of the sports field in metres:
- width (4)
- Length (4)
- Use the given scale to calculate the length of the science classroom block in metres (2)
- Zuki walks from the tuck-shop to his maths classroom, along the broken line Measure how far he walked in metres. (2) [12]
Solutions
-
- Use your ruler to measure the width of the sports field on the map. It is 5 cm wide. ✓
Now use the number scale 1: 500 to determine the actual width of the field:
5 cm × 500 = 2 500 cm ✓✓
(multiply your scaled measurement by the “real” number in the scale ratio)
2 500 cm ÷ 100 = 25 m
The field is 25 m wide. ✓ (4) - On the map, the field is 10 cm long. ✓
10 × 500 = 5 000 cm
5 000 cm ÷ 100 = 50 m ✓✓
The field is 50 m long. ✓ (4)
- Use your ruler to measure the width of the sports field on the map. It is 5 cm wide. ✓
- On the map, the science classroom building is 5 cm long.
5 cm × 500 = 2 500 cm ✓
2 500 cm ÷ 100 = 25 m ✓
The science classrooms are 25 m long. (2) - The broken line is 6,2 cm long on the map.
6,2 × 500 = 3 100 cm ✓
3 100 cm ÷ 1 000 = 31 m ✓
Zuki walked 31 m from the tuck-shop to his maths classroom. (2) [12]
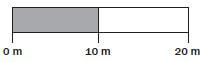
- is represented like this:

Each piece or segment of the bar represents a given distance, as labelled underneath. To use the bar scale:
- You need to measure how long one segment of the bar is on your You must then measure the distance on the map in centimetres.
- Calculate how many segments of the bar graph it works out to be (the total distance measured; divided by the length of one segment).
- Then multiply it by the scale
So, if 1 cm on the bar represents 10 m on ground, and the distance you measure on the map is 3 cm (3 cm ÷ 1 cm length of segment = 3 segments) then the real distance on the ground is 3 × 10 m = 30 m.
e.g. Worked example 2
- You measure a distance of 10 cm on a map with the following bar scale:

If the bar scale is 1 cm:15 m, what is the actual distance on the ground in metres? - You measure a distance of 11 cm on a map with the following bar scale:

If the bar scale is 2 cm : 100 m, what is the actual distance on the ground in metres?

5.1.3 Understanding the advantages and disadvantages of number and bar scales
By now you should understand how to use number and bar scales to measure real dimensions and distances on the ground when given a scale map. What happens if you resize a map? For example, you may want to make small photocopies of a map of your school, to hand out for an event taking place. In the next activity you will explore the effects on the number and bar scales when we resize maps.
Activity 2: Scales and resizing
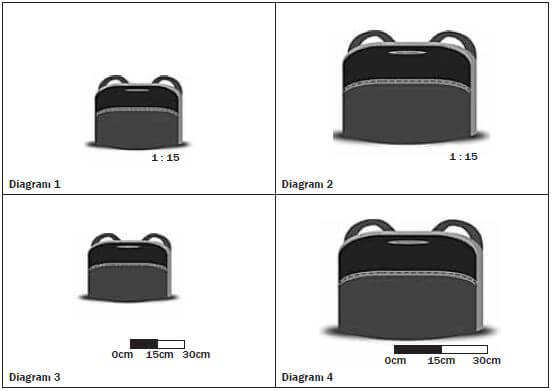
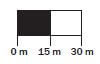
- Measure the width of the school bag in Diagram 1 and use the scale to calculate the real width of the school bag. (1)
- Measure the school bag in Diagram 2 and use the scale to calculate the real width of the school bag. (1)
- What do you notice about the answers for 1 and 2? (1)
- Measure the width of the school bag in Diagram 3 and use the scale to calculate the real width of the school bag. (2)
- Measure the school bag in Diagram 4 and use the scale to calculate the real width of the school bag. (2)
- What do you notice about the answers for 4 and 5? (1) [8]
Solutions
- 2,6 × 15
= 39 cm ✓ - 4 × 15
= 60 cm ✓ - Not the same ✓
- 1,7 : 30 ✓
30 × 2,5 = 44cm ✓✓
1,7 - 2,9 : 30
30 × 4,3 = 44cm ✓✓
3,9 - Same✓✓
If we resize a map that has a number scale on it, the number scale becomes incorrect. If a map is 10 cm wide when printed, and the number scale is 1 : 10 then 1 cm on the map represents 10 cm on the ground. However, if we reprint the map larger, and it is now 15 cm wide, our scale will still be 1 : 10 according to the map, but now 1,5 cm represents 10 cm on the ground (1,5 × 10 = 15 cm = width of map) so the answers to any scale calculations will now be wrong.
- A disadvantage of using a number scale is when resizing maps that use the number scale, it is important to know that the scale changes with the map
- An advantage of a bar scale is when resizing a map that has a bar scale on it, the size of the bar scale will be resized with the map, and it will therefore remain accurate.
- An advantage of the number scale is that we only have to measure one distance (we don’t have to measure the length of one bar segment) and our calculations are usually fairly simple.
- A disadvantage of using the bar scale is that we have to measure the length of one segment and measure the distance on the map. Our calculations can be more complicated because we have to calculate how many segments fit into the distance measured on the map.
5.1.4 Drawing a scaled map when given real (actual) dimensions
We have learnt how to determine actual measurements when given a map and a scale. In this section we will look at the reverse process - how to determine scaled measurements when given actual dimensions, and draw an accurate two dimensional map. Remember that a scale drawing is exactly the same shape as the real (actual) object, just drawn smaller. In the next worked example we will look at how to draw a simple scaled map of a room.
In order to draw a map you need two types of information. Firstly you need to know the actual measurements of everything that has to go onto the map. Secondly you need to know what scale you have to use. The scale will depend on the original measurements, how much detail the map has to show and the size of the map. If you want to draw a map, or plan, of a room in your house on a sheet of A4 paper and include detail of the furniture you would not use a scale of 1: 10 000 (this scale means that 1 cm in real life is equal to 10 000 cm or 1 km in real life).
e.g. Worked example 3
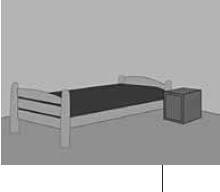
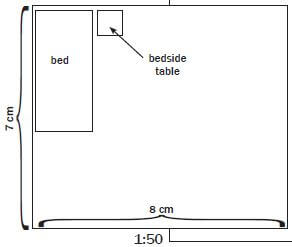
The bedroom in the picture is 3,5 m by 4 m. It has a standard sized single bed of 92 cm by 188 cm. The bedside table is 400 mm square. Draw a floor plan to show the layout of the room. Use the number scale 1 : 50.
Solutions
The scale of 1: 50 means that 1 unit on your drawing will represent 50 units in real life so 1 cm on your drawing will represent 50 cm in real life.
- The width of the room is 3,5 m. Convert 3,5 m to cm:
3,5 × 100 = 350 cm
Use the scale to calculate the scaled width on the map:
350 cm ÷ 50 cm = 7 cm
(Divide the actual, real measurement of the room by the ‘real number’ from the scale.) - The length of the room is 4 m. Convert 4 m to cm:
4 × 100 = 400 cm
Use the scale to calculate the scaled length on the map:
400 cm ÷ 50 cm = 8 cm - The scaled bed is 3,76 cm by 1,84
- The scaled table is 0,8 cm by 0,8 cm.
Activity 3: Drawing a scaled plan
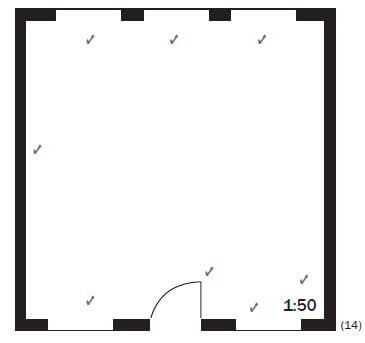
Your school is building a new classroom. The measurements of the classroom are as follows:
length of each wall: 5 metres, width of the door: 810 mm, width of the windows: 1 000 mm
Use the appropriate symbols to draw a plan of the classroom using a scale of 1 : 50. (14)
Place a door, 2 windows in one of the walls and 3 windows in the opposite wall. ( Two walls have no windows in your plan.)
- If the school wants to make blinds out of fabric for the classroom windows, and the blinds are the same size as the windows (1 000 mm wide), calculate the total length of material (in metres) that needs to be bought. (2)
- If the material for the blinds costs R 60 per metre, calculate the total cost of fabric for the blinds. (1)
- The school needs to tile the floor of the Calculate the total area that must be tiled. (2)
- If the tiles come in 4 m2 boxes, how many boxes must the school buy? Explain your (2)
- If the tiles cost R 150 per box, calculate how much the tiles will cost. (1) [22]
Solutions
Conversions [ You must now convert metres and millimetres to centimetres. ]
Real life measurement | Calculation | Measurement on the plan | |
Length of the walls | 5 metres | 5 metres = 500 cm 500 cm ÷ 50 = 10 cm ✓ | 10 cm ✓ |
Width of the door | 810 mm | 810 mm ÷ 50 = 16,2 mm ✓ | 16,2 mm = 1,62 cm ✓ |
Width of the window | 1 000 mm | 1 000 mm ÷ 50 = 20 mm ✓ | 20 mm = 2 cm ✓ |
- There are 5 windows in Each window is 1 000 mm wide.
1 000 mm × 5 = 5 000 mm
There are 1 000 mm in a metre. ✓
5 000 ÷ 1 000 = 5 m ✓ - R 60 per metre × 5 m = R 300 ✓
- Area = length × breadth ✓
= 5 m × 5 m
= 25 m2 ✓ - 25 m2 ÷ 4 m2 = 6,25 boxes ✓
You cannot purchase 6,25 boxes of tiles. You will have to buy 7 boxes. ✓ - 7 × R150 = R 1 050 ✓
The following question papers will assist to ensure further understanding about the SCALE concepts. Skills that were not included on the notes/ worked examples will be learnt through the interaction with these papers.
- Mathematical Literacy P1 Feb/March 2011 Q 6.1.4
- Mathematical Literacy P1 Feb/March 2012 Q 4.2.2
- Mathematical Literacy P1 Feb/March 2013 Q 4.3.2
- Mathematical Literacy P2 Feb/March 2012 Q 1.1.1
- Mathematical Literacy P2 Feb/March 2013 Q 2.1.3
- Mathematical Literacy P1 November 2012 Q 3.3.4 & 5.1.2
- Mathematical Literacy P1 November 2013 Q 4.2.6
- Mathematical Literacy P2November 2010 Q 2.1.3 (b)
- Mathematical Literacy P2 November 2012 Q 4.1.2
Worked example 4
Study the cinema seating plan below and answer the questions that follow.
- If you wanted to book seats for a movie, which seats would you want to sit in?
- Are seats N 11 and N 12 available?
- Which seats offer you and your classmates a good view and why?
- You are going to the movies with a friend in a Name one seat where they can sit, and the seat next to it where you can sit with them.
- Where will you sit if you want to have a very close view of the screen?
- What fraction of row B has been booked? What percentage is this?
Solutions
- H1, H2, H3, H4 or H5.
- They are booked.
- Middle section, because it is not too close or too far from the screen
- For example, the friend could sit in the wheelchair seat next to D1, and you could sit in D1
- Row A
- 3 ≈ 16%
19
Symbols are often used on maps as a short-hand way of representing information. Some symbols that you may be familiar with are: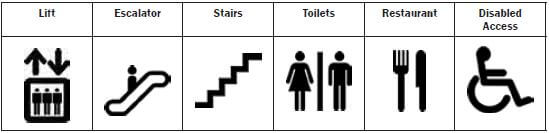
Activity 4: Navigating a shopping mall
Study the map of the ground floor of a shopping centre and answer the questions that follow.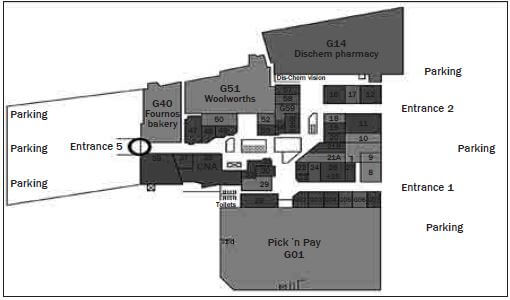
- You want to go to Shop 37 to buy new What store will you find next to it? (1)
- What does “G51 Woolworths” mean on this map? (1)
- Do you think this shopping centre has more than one floor?
Explain your answer. (1) - Where should you park if you want to go to Fournos bakery to buy some fresh bread? (1)
- Name two stores you could buy stationery from and describe how you would get to each of them from Entrance (2)
- If you are at Entrance 2, explain how you would get to the (4)
- You are standing at the entrance of Dis-Chem. Your friend arrives at Entrance 5 and wants to meet Give your friend directions to explain where they will find you. (6) [16]
Solutions
- Shop 35: CNA or shop 39. ✓ (1)
- Woolworths is Shop 51 on the ground floor. ✓ (1)
- Yes - there is an escalator indicated on the map. ✓ (1)
- Near Entrance 5. ✓ (1)
- CNA: Go straight towards Shop
Turn right, go left around the corner at Shop 31.
Go straight. CNA will be on your left. ✓ (1)
Pick n Pay: Go straight passing shops G07 - G02 on your left. Turn left into the entrance of Pick n Pay. ✓ (1) - Go straight, turn left at Shop 18, in front of the ✓ Walk past shops 18 - 23, turn right, ✓ between shops 28 and 29. Go straight down this passageway,✓and the toilets are at the end. ✓ (4)
- Go straight, keeping to the left of the escalators in the middle. ✓ Pass the entrance to Woolworths on your left. ✓ Pass shops 53 - 56 (on your left) ✓ and then turn left in front of the escalators/stairs. ✓ Go straight, passing shops G59, 58 and 57. ✓ Dis-Chem will be in front of you. ✓
We will work through an example of a trip from Kimberley to Beaufort West.
We can see the route on a national map first. Using the bar scale, we can estimate very roughly that the distance is about 500 km. You can also see that the journey will be roughly in a south-westerly direction.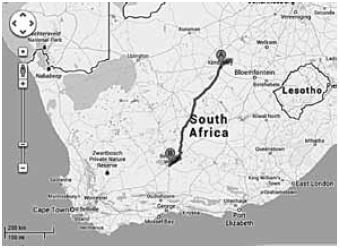
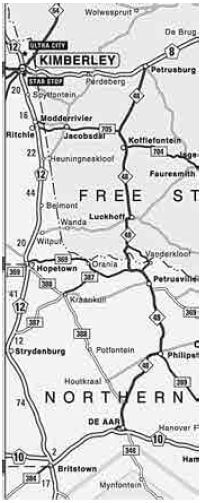
As you travel, you should check that you have followed the directions correctly by looking for new reference points on the map.
Before beginning your trip:
- Find your present location, and where you are going by matching landmarks to the On the map alongside we can see that you need to take the N12 (national road 12) from Kimberley.
- Look at the route you are going to Plan the trip by tracing routes between the two points. This also helps you to become familiar with the places you will travel through and to plan where you will stop for fuel. For example, after leaving Kimberley, you will travel through Spytfontein, Modderrivier and you will pass Ritchie, Heuningneskloof and Belmont before driving through Hopetown and Strydenburg.
- Estimate how long it will take you to get from town to The distances are marked in small numbers between the towns. For example, in the portion of a road map shown alongside, the distance from Kimberley to Spytfontein is 20 km and from Spytfontein to Modderrivier is 16 km.
Clyde lives in Graaff-Reinet. He regularly travels to Adelaide to visit his parents. He also has a family that lives in Jansenville. The map indicates the names of regional roads in rhombuses and main roads in rectangles. National roads are indicated in a pentagon. The actual kilometre distance between sections of the road is also indicated on the map.
Use the map on the previous page to answer the questions that follow.
- Name the regional road Clyde would use to travel from Graaff-Reinet to Adelaide. (1)
- Name THREE towns and/or cities that Clyde would pass on his way to Adelaide. (3)
- Calculate the actual distance between Graaff-Reinet and Jansenville. (4)
- In which general direction is Pearston from Jansenville? (1)
- A distance between two points on the map is 3 cm. The actual (real-life) kilometre distance between the two points is 15 km.
Determine the scale used on the map. (3) [12]
Solutions
- R63 ✓
- Pearsto✓n; Somerset✓East; Cookhouse; Bedford (any three)
- 25 k✓m + 49 k✓m + 10 k✓m = 84 k✓m
- North-easterly ✓ OR NE
- 3 cm : 15 km ✓
= 3 cm : 1 500 000 cm
= 1 : 500 000 ✓
An elevation map is any map which shows the different elevations of an area.
This can be as simple as printing elevations on a road map or as complex as topographical mapping. Most people are actually seeking a simple topographical map when they ask for an elevation map, as they want to see elevation in relationship to geographical features such as rivers, forests, and canyons.
http://blog.maps.com/wordpress/maps/elevation-map/whatisaelevationmap/#sthash. KwLiaenk.dpuf
e.g. Worked example 5
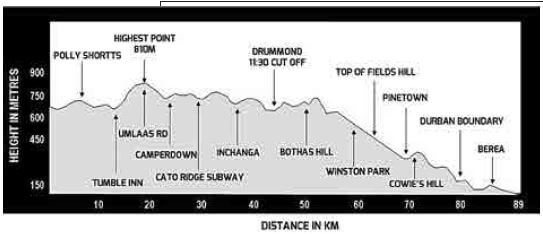
Comrades Marathon
ROUTE & DISTANCE
- It is a “DOWN RUN” starting at the City Hall in Pietermaritzburg and finishing at The Kingsmead Cricket Stadium in Durban. The Comrades Marathon race distance is approximately 89,9 km.
DATE AND TIME OF RACE
- The race will be run on Sunday, 1 June 2014 starting at 05h30 and finishing at 17h30. The race is run from ‘gun to gun’.
Average speed = total distance covered/ time taken
- Which place/road in the maps represents:
- Half the distance of the race?
- The highest point of the route?
- Jomo reaches Durban Boundary 10 hours after the start of the race.
- At what time did he reach Durban Boundary?
- Determine the distance covered by Jomo.
- Calculate Jomo’s average speed (in km/h) during this period?
Solutions
-
- Drummond
- Umlaas Rd
-
- 15h30
- 80 km
- Average speed = total distance covered/time taken
= 80 km/10 h
= 8 km/h
Jomo’s average speed was 8 km/h.
The following question papers will assist to ensure further understanding about the MAPS concepts. Skills that were not included on the notes/ worked examples will be learnt through the interaction with these papers.
- Mathematical Literacy P1 Feb/March 2010 Q 5.1
- Mathematical Literacy P1 Feb/March 2011 Q 6.1
- Mathematical Literacy P1 Feb/March 2012 Q 6
- Mathematical Literacy P2 Feb/March 2012 Q 4
- Mathematical Literacy P1 November 2012 Q 3.3
- Mathematical Literacy P1 November 2013 Q 4.2
- Mathematical Literacy P2November 2010 Q 2.1
- Mathematical Literacy P2 November 2011 Q 3
- Mathematical Literacy P2 November 2012 Q 1 & Q 4
- Mathematical Literacy P2 November 2013 Q 2.1 & Q 2.2
5.3.1 Assembly diagrams and instructions
When you buy certain items from a shop, for example a piece of furniture, sometimes the item is not fully assembled. You would then have to assemble the item yourself. These items usually come with a set of instructions and/ or an annotated diagram.
When we refer to “instructions for assembling”, we are referring to words (usually short sentences) describing how to assemble an item. When we refer to “assembly diagrams”, we are referring to annotated (labelled) pictures that explain in detail how we must assemble an item.
e.g. Worked example 6
In the image below, instructions are given in picture form only. Each number on the diagram represents one step in the assembly process. You are given five written instructions below. In the table below, match each written step to the step number you think it describes.
Step number on image | Statement number/description |
Step 1 | a) Connect the composite video cable to a TV. |
Step 2 | b) Connect the speaker cables. |
Step 3 | c) Connect the power cables of the system and TV to AC power. |
Step 4 | d) Connect the control cable. |
Step 5 | e) Connect the FM antenna. |
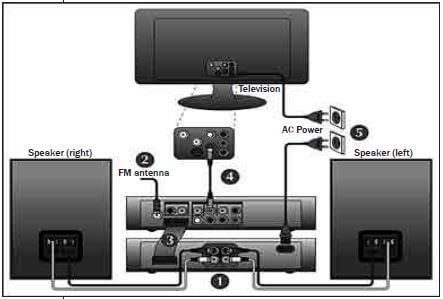
Solution
Step number on image | Statement number/description |
Step 1 | b) Connect the speaker cables. |
Step 2 | e) Connect the FM antenna. |
Step 3 | d) Connect the control cable. |
Step 4 | a) Connect the composite video cable to a TV. |
Step 5 | c) Connect the power cables of the system and TV to AC power. |
e.g. Worked example 7
In a group, study the images below showing how to insert a cellphone’s SIM card and battery, and write a description of each step, based on the images.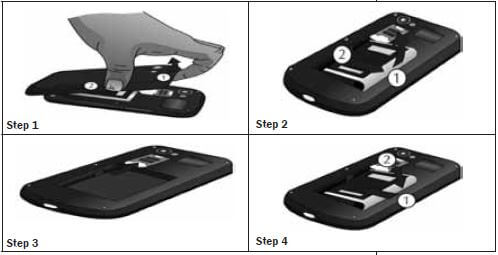
Solutions
Step 1: Place your fingernail in the cover release opening, lift the back cover of the phone up (1) and pull it back (2) to remove it.
Step 2: Lift out the battery by slipping your finger under the side and lifting it up (1) and out (2) of the phone.
Step 3: Slide the SIM card into the SIM card socket inside the phone. Make sure that the card’s gold contacts face downwards.
Step 4: Replace the battery by slipping it back into the phone (1) and pressing it down (2).
Activity 6: Instructions for wiring a plug
Study the assembly instructions given below to wire a plug and answer the questions that follow:
 | 1. Using pliers, carefully bare the ends of the three wires inside the electrical cord for about half a centimetre, by cutting away the plastic insulation. |
 | 2. Gently twist the strands of copper wire with your fingers until each strand is tight. |
 | 3. Remove the new plug cover by either “snapping” it open or unscrewing it. |
 | 4. Unscrew the little screws on each of the plug’s prongs. |
 | 5. Insert the twisted copper wires into the holes in the prongs. |
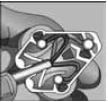 | 6. Tighten the little screw on each of the plug’s prongs. |
 | 7. Make sure the electrical cord is firmly gripped by the arrester clips at the bottom of the plug. |
 | 8. Replace the cover of the plug. |
- What colour wire must be inserted into the top prong? (1)
- What colour wire must be inserted into the left prong? (1)
- What colour wire must be inserted into the right prong? (1)
- What is the main difference between a 2 prong plug and a 3 prong plug? (2)
- Why do you think it is important to wire an electrical appliance correctly? (1) [6]
Solutions
- The green and yellow ✓
- The blue ✓
- The brown ✓
- A 2 prong plug only has two wires, unlike a 3 prong plug, ✓ which has 3.
A two prong plug is also not earthed. ✓ (2) - Appliances that aren’t wired correctly can short circuit ✓ and shock you if you touch them. This can be fatal! (1) [6]
An elevation shows the front, back or side view of a building.
For example, the elevations of a building could look like this:
It is important to understand the layout of floor plans. In order to do this, we can use a key (or legend) that describes the symbols most commonly used on floor plans, as in the key given below.
Sometimes the symbols might look slightly different.
There is a lot of information on a floor plan. Study at the diagram below to understand all of the given information.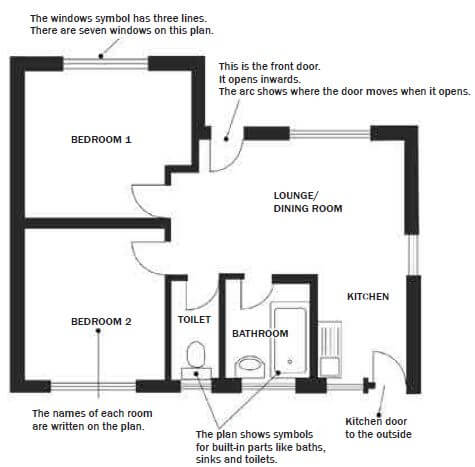
hint
- The floor plan is drawn as if the roof has been lifted off and you’re looking down into the building from the
- Identify the front entrance to the house: imagine opening the front door and walking into each room on the floor
- Doors and windows are two of the most important parts shown on a floor Windows are shown with three parallel lines in a wall.
- Doors are typically shown as a straight line perpendicular to a wall and an arc that connects this line to the This shows which side has the hinges and which room the door opens into.
- The baths, sinks and toilets are shown on the plan, because they are put in when the house is They are called fixtures. This means they are built in and can’t be moved like we move furniture around.
Worked example 8: Drawing a floor plan
The diagram below is an illustration of a part of the bathroom. No windows or doors are shown. The two walls that aren’t visible in the illustration are inside the house.
Use appropriate symbols to draw a rough floor plan of the room in the illustration.
- The plan does not have to be drawn to scale.
- Add a door and a window to your floor plan in any place you think is appropriate.
Solution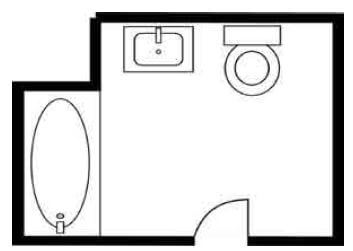
Activity 7: Interpreting a floor plan
Consider the floor plan of a townhouse given below. It contains some errors. Identify as many as you can, and state why each is an error. [20]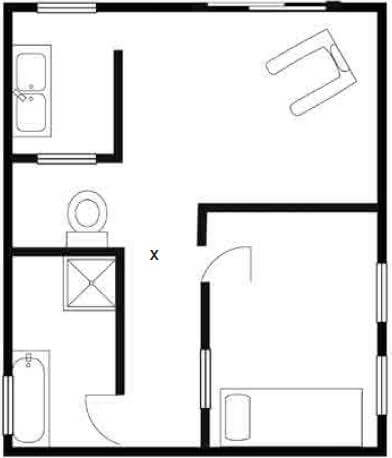
Solution
Room by room:
- The kitchen has a window on the north wall rather than the west wall, meaning that the room will be dark ✓and there is not enough room for wall cupboard units ✓. As there is a window on the south wall as well, the cupboards can only be above and below the sink ✓, so a person working at the sink will be uncomfortable with the cupboard right in front of their face ✓. The sink also is not in a corner ✓, meaning that there is wasted space in the south of the room ✓, because there’s not enough space for a fridge or cupboard there ✓. Furthermore, the placement of the door into the room makes it impossible to put any cupboards on the north wall ✓ The door into the kitchen is just an opening, which is normal in modern houses.
- The toilet is not against a wall which contains water pipes ✓; toilet pipes always run up the exterior (west, in this case) wall, meaning that the toilet won’t work ✓. Furthermore, the toilet does not have a door, which is ✓ Lastly, it is inappropriate to have a window into the toilet from the kitchen ✓. The toilet window is always above the toilet to the outside of the building (with frosted glass). ✓
- The bathroom places the shower in the north-east corner, which means that a pipe to supply hot water would have to run down from the roof in a wall there ✓, which would be risky if someone drilled into the wall to hang a shelf, as it would be hard to guess where the pipe was ✓. Furthermore, a long cold-water pipe will have to run from the west exterior wall to the shower ✓, raising costs ✓ and the same risk of a later accident if the home owner hangs a shelf or The shower should probably be on the west wall as well.✓ The door to the bathroom opens the wrong way✓; it should open against the south wall ✓. Furthermore, the passage is a waste of space✓; the bathroom could be bigger and nicer ✓ if the passage was removed and a door into the bathroom was placed where the passage currently starts (next to the bedroom door, marked “X” on the plan).
- The sliding door in the lounge is on the north This is correct, since houses in the southern hemisphere should be north-facing to get sunlight all day into the living spaces. However, there is a large wall on the west wall which should have a window in it to let in more light.✓
- There is no entrance door into the building apart from the sliding ✓ It is conventional to have one into the kitchen ✓ so that laundry can be taken out back rather than through the house.
- The door in the main bedroom does not open correctly at all and/or is not placed correctly ✓. There are no cupboards in this room ✓; they should be on the north wall (of this plan) ✓. There is a window into the passage ✓; this defeats the privacy of the bedroom (you don’t want people in the passage looking through a window onto your bed). ✓
- Generally, the orientation of the house is ✓ The water pipes and water-using rooms (bathroom, kitchen, toilet), should be on the south side ✓, and the bedroom on the north side ✓, so that the bedroom is more cheerful with light all day.✓ [Any 20]
Packaging and models
When items are packed into a limited space like a box, cupboard or suitcase, how they are packed often determines how many items can fit into the space. A good example of this is trying to pack everything you need for your school day (like your books, sports equipment and food) into your school bag or backpack.
- Sending an extra container costs extra money as well.
- Your books must not be damaged in the process and you have to be able to carry everything yourself.
- These same limits apply to posting a package to a friend or family member. An additional aspect to consider is the cost of the postage which is usually determined by weight.
- If what you are posting is fragile, extra protective material must be packed between the items to make sure they reach the destination unbroken.
e.g. Worked example 9
Vuyo and Sipho’s father own a biscuit business called Biscuits for Africa. It is the June/July school holidays and, to make more pocket money, their father has employed them for one week to help pack the biscuits into boxes so they can be transported to stores.
- Vuyo has to pack small boxes of ginger biscuits into the large shipping boxes for There are 600 small boxes, and Vuyo’s father tells him he can pack 15 boxes of biscuits into one large shipping box. How many large boxes will Vuyo need?
- Sipho has to pack tin cans of chocolate biscuits into the same sized large shipping boxes that Vuyo is He is told he can fit 20 cans into one larger box. If there are 500 cans, how many large boxes will Sipho need?
- Each large shipping box costs R5,50. Which will be cheaper to pack: the ginger biscuits in small boxes, or the chocolate biscuits in cans?
- Vuyo’s and Sipho’s father tells them that each large box can hold a maximum weight of 3,5
- If each small box of ginger biscuits weighs 200 g, how many small boxes can Vuyo pack into a bigger box without exceeding the weight limit?
- If each can of chocolate biscuits weighs 300 g, how many cans can Sipho pack into a bigger box without exceeding the weight limit?
- The boys’ father orders new large shipping boxes that are 45 cm long and 16 cm wide
- If the surface area of the bottom of one small box of ginger biscuits is 25 cm2 (5 cm × 5 cm), how many small boxes can Vuyo fit into only one layer the new large boxes? Draw a scaled diagram (1 : 100) to demonstrate this packaging arrangement.
- If the diameter of one round can is 5 cm, how many cans can Sipho fit (only one layer deep) into the new large boxes? Draw a scaled diagram (1 : 100) to demonstrate this packaging
- Vuyo wants to practise his Maths Literacy skills and rather calculate the area of the bottom of the large box and the small boxes, and divide the larger area by the small one to see how many boxes he can pack
He does the following calculations.
Area of bottom of one small box = 25 cm2. 720 cm2 ÷ 25 cm2 = 28,8 = 28 boxes.
This is different to Vuyo’s initial calculation in Question 5 a).
Why do you think Vuyo got a different answer when he calculated the area?
Solutions
- 600 small boxes ÷ 15 per box = 40 large
- 500 cans ÷ 20 per box = 25 large
- Ginger biscuits require 40 large boxes.
Chocolate biscuits require 25 large boxes
Therefore the chocolate biscuits will be cheaper to pack, because they require fewer large boxes. - (i) 3,5 kg = 3 500 g. 3 500 g ÷ 200 g = 17,5.
But Vuyo can’t pack half a box of biscuits, therefore we round down to the nearest whole number: Vuyo can pack 17 small boxes of ginger biscuits into one large
(ii) 3,5 kg = 3 500 g. 3 500 g ÷ 300 g = 11,67.
But Sipho can’t pack 0,67 cans, therefore we round down to the nearest whole number: Sipho can pack 11 cans of chocolate biscuits into one large box. - (i) Length of large box = 45 cm
45 cm ÷ 5 cm = 9 boxes. Width of large box = 16 cm.
16 cm ÷ 5 cm = 3,2 boxes. Vuyo can’t pack
0,2 of a box, so we round this down to the nearest whole number, 3 boxes.
So Vuyo can fit 9 rows of 3 boxes each. 9 × 3 = 27 boxes.
(ii) Length of large box = 45 cm.
45 cm ÷ 5 cm diameter = 9 cans. Width of large box = 16 cm.
16 cm ÷ 5 cm diameter = 3,2 cans. Sipho can’t pack 0,2 of a can,
so we round this down to the nearest whole number: 3 cans.
So Sipho can fit 9 rows of 3 cans each. 9 × 3 = 27 cans.
Sipho can fit 27 cans of chocolate biscuits into the new large shipping boxes. - Calculating the area of the bottom of the large and small boxes does not take into account the shape of the We can see from the scale diagram in Question 5 a) that it is only possible to fit 27 small boxes into the larger box. 3 boxes in a row (3 × 5 cm = 15 cm) do not fit exactly into the large box (16 cm wide) - there is a small space left which we cannot fill with boxes due to their shape. When dealing with packaging, it is very important to take shapes into account - we cannot just do area calculations without testing our packaging arrangement in reality!
The following question papers will assist to ensure further understanding about the MODELS concepts. Skills that were not included on the notes/ worked examples will be learnt through the interaction with these papers.
- Mathematical Literacy P1 Feb/March 2013 Q 3.2
- Mathematical Literacy P2 Feb/March 2012 Q 5.2.2
- Mathematical Literacy P1 November 2010 Q 2.1
- Mathematical Literacy P1 November 2011 Q 4.2
- Mathematical Literacy P1 November 2012 Q 4.2
- Mathematical Literacy P2 November 2013 Q 1.4 & Q 4.1