Activity 1

Buhle decides to graph her marks for English First Additional Language and for Mathematical Literacy on the same set of axes, for eight tests, two per school term. Look at the graph below and answer the questions that follow.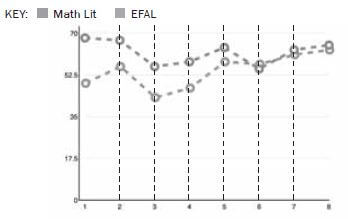

1. What is Buhle’s highest mark? (1)
2. In which subject does Buhle generally score better marks? (1)
3. Does the graph show an overall improvement or an overall decline? (1)
4. What two interesting things can you tell about the marks? (2)
5. What did Buhle score for each subject in test 5? (any two) (2)
6. Is this a continuous or discrete graph, and why? (any two) (2)
7. Is this graph misleading in any way and why? (any two) (2) [11]

Solutions

1.  Approximately 68-70 for Mathematical Literacy, in Test 1. ✓
2. Mathematical Literacy. ✓
3. Overall decline (getting worse). ✓
4. The marks correlate, that is, they seem to go up and down at the same rate. ✓
   They converge; that is, over time, her marks for the two subjects get more similar. ✓
5. 66% (Mathematical Literacy) ✓ and 53% (EFAL) ✓ approximately. (Note to marker: any numbers within 1-2% of these should be marked correct, i.e. 68-64 ✓ and 55-51 ✓ as long as the learner shows that they understand that one is larger than the other by a margin of about 5-6 marks (any two).
6. Discrete ✓; because a learner is not constantly being tested ✓; there are only 8 tests so there cannot be items between the tests ✓; the graph is dotted ✓ (Note to marker: any two are correct) (any two).
7. Yes, because the axes are not marked evenly in steps or increments of 10 ✓, and the marks are all positioned at the top, ✓ which creates the impression that Buhle is scoring well, whereas her marks are in fact just a bit better than average. ✓ (Any two). (2) [11]

Activity 2

Pieter wants to start a lift club, and he wants to know how many people he needs to give a lift to in his car in order to break even on petrol costs. People are not willing to contribute more than R 20 per day, and he gains a new passenger each week (starting with one passenger). Answer the questions that follow.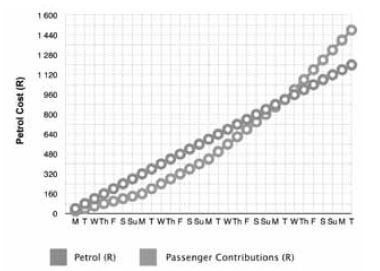

1. How many people does he need to give a lift to to break even, if his petrol costs R 1200 per month? Why? (2)
2. What value or quantity does the curved line show? (1)
3. What day of the month does he break even? Assume that the first Monday is the 1st of the month. (1)
4. Why does the curved line overtake the straight line? (1)
5. What profit does he make each month? Use the income/expenditure/ profit formula. (3)
6. Assuming that Pieter has to service his car every six months at a cost of R 1000, is this still a viable business option for him? Why? (3) [11]

Solutions

1. Three. ✓ Because at the end of the week of having transported three people, he starts making a profit. ✓
   Marker: bonus mark if they observe that two persons would never get him a profit. ✓
2. Cumulative passenger contributions in Rands ✓ OR How much his passengers are paying. ✓ (any 1)
3. On day 23 / The 23rd. ✓
4. Because he is now making a profit ✓ OR The passenger contributions or fares start to exceed his cumulative petrol cost. ✓ (any 1)
5. R 1480 (income) ✓ - R 1200 (expenditure) ✓ = R 280 (profit). ✓
6. Since he makes R 280 profit each month, by six months, he would have made R 1680. ✓
   Since the service costs R 1000, he will still make a profit of R 680 after 6 months ✓, so it is still a viable business. ✓

Activity 3

Answer the questions below about this graph.
Spend a few minutes looking at the graph before you start. Write the scale on the graph and some other quick notes, to help you understand the graph.
Hint

• Use a ruler and pencil to help you read off the graph grid correctly.

1.                              
   1. How many blocks represent 10% on the vertical axis? (2)
   2. How many blocks represent 1% on the vertical axis? Why? (3)
2. Describe the scale on the horizontal axis. (2)
3. What percentage is reached at 10 hours? (2)
4. Where does the line begin? (1)
5. Give the values at A and B in percentages and hours. Give your answer in two ordered pairs. (7)  [17]

Solutions

1.                                              
   1. 1 large block, which has 5 small blocks, represents 10%.
   2. One half of a small block represents 1%. This is because one small block represents 10% ÷ 5 = 2%.
2. 1 large block represents 1 hour ✓. This means  that one small block represents 0,2 h or one fifth of an hour.    ✓
3. The percentage at 10 hours is halfway between 80% and 90%, so it is 85%. ✓
4. The line begins at 0 h and 2%. ✓
5. A is at exactly 5 hours. A is between 40% and 50%. It is 2 small squares up from 40. Each small square represents 2%, so the 2 squares show 4%. A is (5; 44) 

   and B is (7; 60). (7)[17]