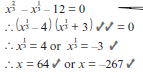EXPONENTS AND SURDS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- The number system
- Working with irrational numbers
- Exponents
- Exponential equations
- Equations with rational exponents
- Exam type examples
To understand exponents and surds, you need to revise the number system thoroughly.
1.1 The number system
1.1.1 Real numbers
The numbers that we work with every day are called real numbers.
The set of real numbers has subsets shown in the Venn diagram:
- Natural Numbers
ℕ = {1; 2; 3; …} (positive whole numbers) - Whole Numbers
ℕ0 = {0; 1; 2; …} (Natural numbers and 0) - Integers
ℤ = {… ;–3; –2; –1; 0; 1; 2; 3; …} - Rational Numbers
A rational number is a Real number which can be written in the form a/b where a, b ∈ Z and b ≠ 0. The rational numbers include all the
integers.
e.g 1
- Irrational Numbers
- Irrational numbers are numbers that cannot be written
- as fractions.
- All decimals that do not terminate or recur are irrational.
HINT: Pi (π)is an interesting irrational number.
NOTE: 22/7 and 3,14 are approximate rational numbers that have a value close to π.
So 22/7 ≠ π and 3,14 ≠ π
All terminating, recurring decimals are rational numbers examples:
e.g 2. √5 = 2,23606… pi (π) = 3,141592… - They have decimals that continue indefinitely with no pattern.
- Look at these numbers on a calculator.
- The calculator will round them off. However, they continue indefinitely without a pattern.
- The symbol for the irrational numbers is ℚ′, which means the complement of ℚ or not ℚ.
- Real Numbers
The set of real numbers, ℝ, is the set of all rational and irrational numbers together.
We can also write ℝ = ℚ ⋃ ℚ′
e.g 3. –3; – √7 ; –1¼; –1;0; ½ ; 1; √2 ; 2; 3; π
1.1.2 Non-real Numbers
The square root (or any even root) of a negative number, is a non-real number.
e.g 4. √ −25 is a non-real number.
4√ −100 is a non-real number
6√−120 is a non-real number
• The calculator will show an error.
e.g 5. x2 + 5x + 9 = 0
Use the quadratic formula to find the values of x:
√−11 is a non-real number so the value of x is non-real. There are no real roots for the equation, so the graph of the function y = x2 + 5x + 9 has no intercepts with the x-axis.
You will learn more about the nature of roots in Unit 2.
Some quadratic equations do not have real roots, but some do
Any number = undefined. The calculator will also show an error.
0
1.2 Working with irrational numbers
1.2.1 Surds
All square roots; cube roots, etc. that they are not rational are called surds.
√2 ; √3 ; √5 ; √6 ; √7 ; √8 ; are all surds.
Surds are real numbers which when expressed as decimals are nonrecurring and non-terminating.
We can work out where a surd lies between two integers on a number line.
e.g 6. √1 = 1 and √4 = 2, so √2 lies somewhere between 1 and 2.
3√64 = 4 and 3√125 = 5, so 3√102 lies between 4 and 5.
We can show their approximate positions on the number line:![]()
Some roots or radical numbers are rational and are not surds:
e.g 7. Examples of roots that are not surds include:
√1 = 1; √4 = 2; √9 = 3; 3√8 = 2; 4√81 = 3
1.2.2 Simplifying surds
e.g 8
- √5 × √3 = √15 (1)
- ( √5 ) 2 = √5 × √5 = 5 (1)

- √a2 − b2 cannot be simplified
- 3√274 = 3√(33 )4 = 3√312 = 312/3 = 34 = 81 (2)
- √9 + 16 = √25 = 5 (1)
- √9 + √16 = 3 + 4 = 7 (1)
HINT: √9 + 16 ≠ 3 + 4
Activity 1
Write in simplest form without using a calculator (show all working).
- √8 × √2
- 3√4 × 3√2
- 9 + √45
3 - (2 + √5 ) (2 − √5 )
[10]
Solutions
|
1.2.3 Rationalising a denominator
When a fraction contains a surd in the denominator, you can change the denominator to a rational number. This is called ‘rationalising the denominator’.
If you multiply the numerator and the denominator by the same surd, you are not changing the value of the number. You are multiplying by 1
(i.e √2 = 1) to change what the number looks like, not its value. Doing this can give you a rational denominator.
√2
e.g 9. Rationalise the denominator of √3
√2
√3 = √3 × √2 = √3 × √2 = √6 (1)
√2 √2 √2 2 2
Now the denominator is a rational value.
Check on a calculator: √3 = √6 = 1,2247…
√2 2
e.g 10.
3
√3 − 1
(has an irrational number in denominator)
= 3 × √3 + 1
√3 − 1 √3 + 1
(multiply by √3 + 1 √3 + 1, since 1= √3 + 1)
√3 √3
= 3(√3 + 1) = 3 √3 + 3
( √3 − 1)( √3 + 1) 3 + 3 − √3 − 1
(notice how the surd terms cancel)
= 3 √3 + 3 (2)
2
(now the denominator is rational)
If the denominator is √3 − 1,multiply by √3 + 1 .This will give us the difference of two squares.
√3 + 1
Activity 2 Interpret a graph
| 1. Complete the table for each number by marking the correct columns. | |||||||
| Nonreal number | Real number ℝ | Rational number ℚ | Irrational number ℚ′ | Integer ℤ | Whole number ℕ0 | Natural number ℕ | |
| a) 13 | |||||||
| b) 5,121212… | |||||||
| c) √–6 | |||||||
| d) 3π | |||||||
| e) 0 = 0 9 | |||||||
| f) √17 | |||||||
| g)3√64 = 4 | |||||||
| h) 22 7 | |||||||
(23)
2. Which of the following numbers are rational and which are irrational?
- √16
- √8
- √ 9
4 - √6¼
- √47
- 22
7 - 0,347347…
- π − (− 2)
- 2 + √2
- 1,121221222… (10)
[33]
Solutions
| 1. Complete the table for each number by marking the correct columns. | |||||||
| Nonreal number | Real number ℝ | Rational number ℚ | Irrational number ℚ′ | Integer ℤ | Whole number ℕ0 | Natural number ℕ | |
| a) 13 | ✓ | ✓ | ✓ | ✓ | ✓(5) | ||
| b) 5,121212… | ✓ | ✓ | (2) | ||||
| c) √–6 | ✓ | (1) | |||||
| d) 3π | ✓ | ✓ | (2) | ||||
| e) 0 = 0 9 | ✓ | ✓ | ✓ | ✓ | (4) | ||
| f) √17 | ✓ | ✓ | (2) | ||||
| g)3√64 = 4 | ✓ | ✓ | ✓ | ✓ | ✓ (5) | ||
| h) 22 7 | ✓ | ✓ | (2) | ||||
2.
- √16 (rational)
- √8 (irrational)
- √ 9 = 3 (rational)
4 2 - √6¼ = √25 = 5 (rational)
4 2 - √47 (irrational)
- 22 (rational)
7 - 0,347347…(rational, because it is a recurring decimal) 3 (1)
- π − (− 2) (irrational, because π is irrational) 3 (1)
- 2 + √2 (irrational, because √2 is irrational) 3 (1)
- 1,121221222…(irrational, because it is a non-recurring and non-terminating decimal) 3 (1)
[33]
1.3 Exponents
The exponent of a number tells us how many times to multiply the number (the base) by itself.
So a2 = a × a
a3 = a × a × a
an = a × a × a × … n times
e.g. 11
34 read as: three to the power of 4, or 3 exponent 4 which is equal to 3 × 3 × 3 × 3 = 81
1.3.1 Rules of exponents
These rules work for exponents that are integers, rational numbers or irrational numbers.
| 1. a m × a n = am + n To multiply two powers with same bases, add their exponents. | a 5 × a 3 = a 5 + 3 = a8 3 5 × 3 3 = 3 5 + 3 = 38 |
| 2. a m ÷ a n = am – n To divide two powers with same bases, subtract their exponents. | a 8 ÷ a 2 = a 8 – 2 = a 6 |
| 3. (am)n = amn To raise a power to an exponent, multiply the exponents. (ab)m = (am bm) ( a )m = a m b bm | ( a 4 ) 3 = a 4 × 3 = a 12 ( a 2 × b 3 ) 5 = a 2 × 5 . b 3 × 5 = a 10 . b 15 ( a 5 /b 2 ) 3 = a 5×3 = a 15 b 2×3 b 6 |
| 4. a0 = 1, Any base raised to 0 is 1 | (b ) 0 = 1 ; ( 3 ) 0 = 1 ; (5 a 2 b 3 ) 0 = 1 |
| 5. 1 = a−n an A positive exponent in the denominator is the same as a negative exponent in the numerator. ( a ) -m = (b)m b a | |
| 6. To find the root of a power, divide the exponents. |  |
1.3.2 Algebraic expressions with exponents
Remember to work in this order:
signs → values → variables
| Values | Variables | Answer | |
| a) –3a3b2 × - 4a4b4 | -3× - 4 = 12 | a3b2 × a4b4 = a7b6 | = +12a7b6 |
| b) 12x5y8 ÷ - 4x2y4 | 12 ÷ - 4 = –3 | x5y8 ÷ x2y4 = x3.y4 | = - 3x3y4 |
| c) (−3a3b2)3 | (–3 )3 = –27 | (a3b2)3 = a 9 b 6 | = − 27a9b6 |
| d) 4√16a16 | 4√16 = 2 (24 = 16) | 4√a16 =a4 | = 2a4 |
Where necessary, we work out the inside set of brackets first and follow the order of operations:
B O D M A S Brackets/Of, Division/Multiplication/Addition/Subtraction
Activity 3
Calculate
- −3 (( −2a3)2 + √9a12) √9a12 = (32a12)½
- 5(2a4)3
(5a3)2 − 5a6 [5]
Solutions
|
1.3.3 Prime factors
When the bases are different, we can write each base as a product of its prime factors.
Remember: A prime number has only two different factors.
A composite number has more than two factors.
The number 1 is neither a prime number nor a composite number.
Prime numbers: 2; 3; 5; 7; 11; 13 …
Every composite number can be written as the product of prime numbers.
This helps us to factorise and to simplify.
e.g 12.
4 = 22; 6 = 2 × 3; 8 = 23; 9 = 32; 10 = 2 × 5; 12 = 22 × 3
24 = 8 × 3 = 23 × 3
| NOTE: To find the factors of 2 700, divide by the lowest prime that is a factor eg 2; then move onto 3; then 5 etc. 2 700 = 22 × 33 × 52 Find out how your scientific calculator can calculate the prime factors of a number for you. |
e.g 13.
Express 72x−2 in prime factors
72 x−2 = (23.32)x−2
= 23(x−2).32(x−2)
= 23x−6.32x−4
1.3.4 Working with negative exponents
It is easier to write answers with positive exponents, so we use the exponent rule:
1 = a-n and 1 = an
an a-n
This also means that ![]()
Activity 4
Simplify the following. Write answers with positive exponents where necessary.
- a -3
b-2 - 4a7b-4c-1
d–2e5 - x–1+ y-1
[5]
Solutions
|
1.3.5 Working with surd (root) signs
The exponential rule can be used to simplify certain expressions.
Activity 5
1. Rewrite these expressions without surd signs and simplify if possible.
- 3√5
- 4√16
- 3√–32
[3]
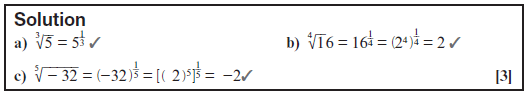 e.g. 14.
e.g. 14.
3√ −27 = − 3 because (–3)3 = –27 ∴ 3√ −27 is real
4√ −16 is non-real
1.3.6 Watch out for these common mistakes!
| Correct | Warning |
| 1. 2n.3n = 6n | 2.3n ≠ 6n |
| 2. 34 × 35 = 39 | 34 × 35 ≠ 99 |
| 3. 410 ÷ 45 = 45 | 410 ÷ 45 ≠ 42 410 ÷ 45 ≠ 15 410 ÷ 45 ≠ 12 |
| 4. (3b)n−1 = 3n–1bn –1 | (3b)n−1 ≠ 3.bn–1 |
| 5.(a + b)2 = a2 + 2ab + b2 | (a + b)2 ≠ a2 + b2 |
| 6. √16×16 = 4x8 | √16×16 ≠ 4 x 4 ] |
| 7.√a2 + b2 = (a2 + b2)½ ≠ a + b 8. 3 ×−3 = 3 x3 9.( x + y)−2 = 1 (x + y)2 | √a2 + b2 ≠ a + b e.g.√52 − 32 ≠ 5 − 3 = 2 because √52 −32 = √25 − 9 = √16 = 4 3x−3 ≠ 1 3x3 (x + y)−2 ≠ x−2 + y−2 |
NOTE: A surd is also called a radical.
1.3.7 Simplification of exponential expressions
Activity 6
Simplify the following and leave answers with positive exponents where necessary:
(a4)n–1. ( a2b)–3n
(ab)–2n. b–n
[4]
| Solution (a4)n–1. ( a2b)–3n = a4n−4 . a– 6n . b−3n (ab)–2n. b–n a−2n. b−2n . b–n = a4n–4 – 6n +2 n . b −3n + 2n + n = a−4 . b0 = 1 . 1 = 1 a4 a4 [4] |
1.3.8 Algebraic fractions with exponents
1. Expressions with only products of terms
- Factorise the terms using prime factors.
- Use laws of exponents.
e.g. 15 2. Expressions with terms added or subtracted
2. Expressions with terms added or subtracted
- First try to factorise both the numerator and denominator.
- Use laws of exponents.
- Cancel any common factors.
e.g. 16
Activity 7
Simplify the following and leave answers with positive exponents where necessary:
- 273 - 2x.9x-1
812-x - 6.5x +1 - 2.5x +2
5x+3 - 22009 − 22012
22010 [13]
Solutions
|
1.4 Exponential equations
Solving equations where x is part of the exponent:
- Write the powers as products of prime factors.
- Aim to get ONE power with the same base on each side of the equation.
- Equate the exponents.
- Solve for x.
e.g. 17
Solve for x
1. 2x = 8 write 8 as a power of 2
2x = 23 get the same base on each side
∴ x = 3 equate the exponents
2. 52 x+1 − 125 2 x−3 = 0 equate the two powers
52 x+1 = 125 2 x−3
52 x+1 = (53)2x−3 write with prime bases
52 x+1 = 56 x−9
∴ 2x + 1 = 6x –9
∴ –4x = –10
∴ x = 5
2

5. 3 2x − 12. 3 x + 27 = 0
∴ 3 x . 3 x − 12. 3 x + 27 = 0
Method 1:
∴ 3x.3 x − 12. 3x + 27 = 0
(3x − 9 ) (3x − 3 ) = 0
3x = 9 or 3x = 3
3x = 32 or 3x = 31
∴ x = 2 or x = 1
Method 2:
∴ 3x.3 x − 12. 3x + 27 = 0
let 3 x = k ∴ k.k − 12k + 27 = 0
∴ k2 − 12k + 27 = 0
( k − 9 ) ( k − 3 ) = 0
∴ k = 9 or k = 3
but = k ∴ 3x = 9 or 3x = 3
∴ x = 2 or x = 1
[24]
Activity 8
Solve for x:
- 3 ( 9x+3 ) = 272x–1
- 32x–12 = 1
- 2x = 0,125
- 10x ( x+1 ) = 100
- 5x + 5x+1 = 30
- 5 2+x – 5x = 5x. 23 + 1
- 5x + 15.5 −x = 2
{31]
Solutions
|
1.5 Equations with rational exponents
1.5.1 Tips
- When working with equations, you must do the same operation to both sides of the equation.
- Get the variable with the fraction exponent on one side by itself.
- Get x by itself by changing the fraction exponent to an exponent of 1.
- Do this by choosing an exponent for both sides, so that xm/n becomes x1 .
e.g 18 Activity 9
Activity 9
Solve for x: 1.5.2 Exponential equations with surds
1.5.2 Exponential equations with surds
e.g. 19
Solve for x:
3 √x + 2 + x = 2
[7]
Solution Check: |
Activity 10
Solve these equations and check your solutions.
1. √3x + 4 − 5 = 0 (3)
2. √3x − 5 − x = 5 (5)
[8]
Solutions
|
1.6 Exam type examples
Activity 11
What you need to be able to do:
- Use the laws of exponents to simplify expressions
- Calculate with negative powers
- Multiply and divide powers
- Add and subtract powers
- Solve exponential equations, including those with rational exponents
- Simplify surds and do operations with surds
- Rationalise the denominator if necessary
- Solve equations involving surds.