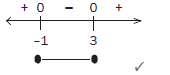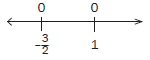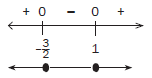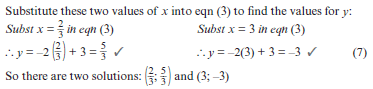ALGEBRA GRADE 12 NOTES - MATHEMATICS STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- Algebraic expressions
- Addition and subtraction
- Multiplication and division
- Factorising
- Notes on factorising a trinomial
- Quadratic equations
- Quadratic inequalities
- Simultaneous equations
- The nature of the roots
2.1 Algebraic expressions
Algebraic expressions are made up of constants, variables and number operations (add, subtract, divide and multiply).
The variables are shown with letters such as x, y, a, b, p, m, n, etc.
The terms in an algebraic expression are separated by a plus or a minus sign.
e.g. 1
- 2x + 3y is an algebraic expression with two terms which are 2x and 3y.
- 2x(3y) is only one term.
- (2x + 3y)(2x – 3y) is also only one term because it is two expressions in brackets multiplied together. The brackets are not separated by + or –.
- √2x − 3 is also an algebraic expression with one term because square roots can be written as exponents. √2x − 3 = (2 x − 3)½
2.2 Addition and subtraction
Check that you know these facts:
- We can add or subtract like terms.
- If the terms are like, we add or subtract the coefficients.
- Like terms have the same variables (letters) and the variables must have the same exponents.
e.g. 2
3x + 5x = 8x
–3a + 10a = 7a
6x2 y + 3x − 10x2 y = −4x2 y + 3x
a + c = ad + cb
b d bd
We cannot add or subtract unlike terms.
2.3 Multiplication and division
Check that you know these facts:
positive number × positive number = positive answer. 3x × 5y2 = 15xy2
positive number × negative number = negative answer. 3x × –5y2 = –15xy2
negative number × positive number = negative answer. –3x × 5y2 = –15xy2
negative number × negative number = positive answer. –3x × –5y2= 15xy2
a x c = ac
b d bd
e.g. 3
6x × 3 = 18x
7y 5z 35yz
e.g 4
6 + 3 = 6x3z + 3(2y) = 18xz + 6y
8y 12z 24yz 24yz
a ÷ c = a x d = ad
b d b c bc
Multiply numerators and multiply denominators. Simplify if possible.
The distributive law:
c(a + b) = c × a + c × b = ac + bc
e.g 5
–3x(5x – 6y) = –15x2 + 18xy
(x + y)(a + b) = ax + bx + ay + by
e.g. 6
(2x + y)(3x – 2y) = 6x2 – 4xy + 3xy – 2y2 = 6x2 – xy – 2y2
2.4 Factorising
What does it mean to ‘factorise an expression’?
It means to write the expression as a product of its factors.
e.g. 7
Here are ways to factorise an expression:
- Find the common factor:
9x2 – 6xy2 = 3x(3x – 2y2) - Factorise by grouping in pairs and then finding a common factor:
3xy – 2x + 3y – 2
= 3xy + 3y – 2x – 2
= 3y(x + 1) – 2(x + 1) When you take out a negative factor, signs in bracket change.
= (x + 1)(3y – 2) - Factorise a difference of two squares:
16x2 – y2 = (4x – y)(4x + y) - Factorise a difference of two cubes:
8x3 – y3 = (2x – y)(4x2 + 2xy + y2) - Factorise a sum of two cubes:
27a3 + 64b3 = (3a + 4b)(9a2 – 12ab + 16b2) - Factorise a trinomial:
9x2 + 5x – 4 = (9x – 4)(x + 1)
When factorising, always take out a common factor first, if possible. Then look to factorise the difference of two squares or the sum/difference of two cubes or a trinomial.
It is useful to use ‘FOIL’ (multiply FIRST terms, OUTER terms, INNER terms and LAST terms).
2.5 Notes on factorising a trinomial
The following steps will explain how to factorise a trinomial:
e.g. 8
Factorise 3x2 + 11x + 6
Step 1: Multiply the coefficient of x2 and the constant value (+3 × +6 = 18).
Step 2: Write down all the products of 18:
10 × 1
9 × 2
6 × 3
Step 3: We will use 9 × 2, because 9 + 2 = 11, the middle term.
Step 4: We write the middle term (11x) as 9x + 2x
∴ 3x2 + 11x + 6
= 3x2 + 9x + 2x + 6......we wrote the 9x first, followed by the 2x
(We write the 9x first and the 2x second because: There is a common factor between 3x2 and 9x.
There is a common factor between 2x and 6.)
Step 5: We now group the four terms and factorise by taking out a common factor.
3x2 + 9x + 2x +6
= 3x(x + 3) + 2(x + 3)
= (x + 3)(3x + 2)
e.g. 9
Factorise 4x2 + 9x – 13
Step 1: Multiply the coefficient of x2 and the constant value (+4 × –13 = –52).
Step 2: Write down all the products of 52:
52 × 1
26 × 2
13 × 4
Step 3: We will use 13 × 4, because 13 – 4 = 9, the middle term.
Step 4: We write the middle term (9x) as –4x +13x
∴ 4x2 + 9x – 13
= 4x2 – 4x + 13x – 13......we write the –4x first, followed by the 13x
(We write the –4x first and the 13x second because:
There is a common factor between 4x2 and –4x. There is a common factor between 13x and –13 .)
Step 5: We now group the four terms and factorise by taking out a common factor.
4x2 – 4x + 13x – 13
= 4x(x – 1) + 13(x – 1)
= (x – 1)(4x + 13)
e.g. 10
Factorise 8x2 – 18x + 9
Step 1: Multiply the coefficient of x2 and the constant value (+8 × +9 = 72).
Step 2: Write down all the products of 72:
72 × 1
36 × 2
24 × 3
18 × 4
12 × 6
9 × 8
Step 3: We will use 12 × 6, because –12 – 6 = –18, the middle term.
Step 4: We write the middle term (–18x) as –12x – 6x or –6x – 12x
∴ 8x2 – 18x + 9
= 8x2 – 12x – 6x + 9......we write the –4x first followed by the 13x
(In this example, we can write –12x first and then –6x or –6x first and then –12x. We have a common factor between 8x2 and –12x and between –12x and 9. We have a common factor between 8x2 and –6x and between –6x and 9.)
Step 5: We now group the four terms and factorise by taking out a common factor
8x2 – 12x – 6x + 9
= 4x(2x – 3) – 3(2x – 3)
= (2x –3)(4x – 3)
Activity 1
Factorise each of the following completely:
- 12x2 + 17x + 6
- 5x2 – 23x – 10
- 9x2 + 5x – 4
- 12x2 – 11x + 2
- 5x2 – 45
- 2x3 + 16
- 6x3 – 13x2 + 5x
[16]
Solutions
|
2.6 Quadratic equations
e.g .11
Here are some quadratic equations:
- x2 + 5x + 6 = 0
- 3x2 – 7x = 12
- 3x(x – 9) + 2 = 5x 3x × x = 3x2 so the equation has x2 as its highest power of x
Quadratic equations can be put into the standard form: ax 2 + bx + c = 0
e.g. 12
- x2 + 5x + 6 = 0 So a = 1, b = 5 and c = 6
- 3x2 – 4x = 12
3x2 – 4x – 12 = 0 So a = 3, b = –4 and c = –12 - 3x(x – 9) + 2 = 5x
3x2– 27x + 2 – 5x = 0
3x2 – 32x + 2 = 0 So a = 3, b = –32 and c = 2
2.6.1 Solving a quadratic equation by factorising:
What does it mean to ‘solve a quadratic equation’?
It means to find the unknown value(s) of x in a quadratic equation. The x-values in a quadratic equation are also called the roots of the equation when the equation is equal to zero.
e.g. 13
Solve for x:
x2 – 7x = –10
x2 – 7x + 10 = 0 Write in standard form and equal to 0
x2 – 5x – 2x + 10 = 0 Factorise the trinomial
x(x–5) –2(x–5) = 0
(x – 5)(x – 2) = 0
∴x – 5 = 0 or x – 2 = 0
x = 5 ∴x = 2
Activity 2
Solve for x:
- x(x + 3) = 0
- x(2x – 5) = 12
- 2x2 + x − 6 = 0
- 2x2 = 32
- 3x + 1/x = 4, x ≠ 0
- 2√x − 3 = x − 3
[22]
If (A) × (B) = 0, then either A = 0 OR B = 0.
Solutions
|
Check your answers:
x = 7
LHS = 2 √7 − 3 = 2 √4 = 2(2) = 4 RHS = 7 − 3 = 4 ∴ x = 7 is a solution
x = 3
LHS = 2 √3 − 3 = 2 √0 = 0 RHS = 3 − 3 = 0 ∴ x = 3 is a solution
If a quadratic equation cannot be factorised, there are other ways to find the roots or solutions. Sometimes the solutions do not exist!
2.6.2 Completing the square
e.g.14
Write y = 3x2 + 12x + 9 in the form y = a(x + p)2 + q.
To do this, we can follow a few steps:
y = 3x2 + 12x + 9 To complete the square, the coefficient of x2 must be one (1).
We take 3 out as a factor so that the coefficient of x2 is one.
y = 3[x2 + 4x + 3] Take (half of the coefficient of x) and square the number. Add and subtract this answer to keep the equation balanced.
The coefficient of x is +4.
Halving 4 = 2. (+2)2 =4.
y = 3[x2 + 4x + (+2)2 + 3 – (+2)2] Thus, add 4 and subtract 4.
y = 3[x2 + 4x + 4 + 3 – 4]
= 3[x2 + 4x + (+2)2 + 3 – 4] Now we can complete the square by factorising
(x + 2)2
y = 3[(x + 2)2 + 3 – 4]
y = 3[(x + 2)2 – 1]
y = 3(x + 2)2 – 3
We have now written y = 3x2 + 12x + 9 as y = 3(x + 2)2 – 3.Therefore, we have written y = ax2 + bx + c in the form y = a(x + p)2 + q with a = 3,p = 2 and q = -3.
The quadratic equation y = 3x2 + 12x + 9 helps us to identify the y-intercept, while the form y = 3(x + 2)2 – 3 helps us to identify the turning point. Refer to graphs in unit 4 on Functions.
Activity 3
- What term can be added to the following equations to make a complete square?
- 0 = x2 – 8x + ?
- y = x2 + 9x + ?
- y = x2 -b/a x + ?
- Solve for x by using the method of completing the square.
- –3x2 + 5x + 4 = 0
- ax2 + bx + c = 0 [17]

2.6.3 Solving quadratic equations using the formula
Some quadratic equations cannot be factorised, but there is another way to find the roots of the equation.
e.g.15
Can you find factors for this quadratic equation: x2 – 5x + 3 = 0?
There are no rational numbers that can be multiplied to get 3 and added to get 5, therefore use the quadratic formula to solve the equation.
| The standard form of the quadratic equation ax2 + bx + c = 0 is used from which the formula is derived: x = − b ± √b2 − 4ac 2a |
For x2 – 5x + 3 = 0 a = 1, b = –5 and c = 3
Substitute these values for a, b and c in the formula:
x = − ( − 5) ± √(− 5 ) 2 − 4(1)(3)
2(1)
x = 5 ± √25 − 12
2
x = 5 ± √13
2
x = 5 + √13 OR x = 5 −√13
2 2
Activity 4: Interpret a graph
Solve for x (correct to two decimal places):
4x2 – 8x = 7
2x (3x + 5) – 11 = 0 [9]
Solutions |
e.g.16
If 2/3 is a root of the equation 12x2 – kx – 8 = 0, determine the value of k.
2.7 Quadratic inequalities
Solving quadratic
To solve quadratic inequalities
- Get the inequality into the standard form ax2 + bx + c > 0 or ax2 + bx + c < 0 or ax2 + bx + c ≤ 0 or ax2 + bx + c ≥ 0
- If the value of a < 0, multiply the equation by –1.
- Factorise the inequality when this is possible or
- use the quadratic formula to obtain the critical values.
e.g 17
Solve for x if x2 < 25
Method 1
x2 < 25
x2 – 25 < 0
(x – 5)(x + 5) < 0
(If we multiply an inequality by a negative, the inequality sign swaps: If -5 < 7, then after being multiplied by (-1), ∴ 5 > –7)
The critical values are where the expression x²–25 is equal to zero.
Therefore the critical values are –5 and 5.
We now indicate –5 and 5 on a number line.![]()
We know that the expression x²–25 = 0 at –5 and 5. We can indicate this on the number line.
Our next step is to choose values less than –5, values between –5 and 5 and values greater than 5 and substitute it into the expression x²–25. If the answer is positive, then we indicate + on the number line. If the answer is negative, we indicate – on the number line.
We have to solve for x where x2 – 25 < 0. The solution on the number line is the interval where we see a negative. This happens between –5 and 5.
Therefore the solution is : –5 < x < 5
| If x = –10, then (–10)² – 25 = 75 > 0 ∴ + If x = –6, then (–6)² – 25 = 11 > 0 ∴ + If x = –3, then (–3)² – 25= –16 < 0 ∴ – If x = 2, then (2)² – 25= –21 < 0 ∴ – If x = 7, then (7)² – 25 = 24 > 0 ∴ + If x = 9, then (9)² – 25 = 56 > 0 ∴ + |
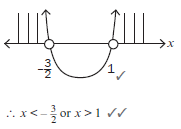
OR ALTERNATIVE METHOD by using a rough sketch of the parabola:
Above the x-axis y is positive
On the x-axis y is zero
Below the x-axis y is negative
e.g. 18
Solve for x if x2 < 25
x2 < 25
x2 – 25 < 0 Get 0 on RHS
(x – 5)(x + 5) < 0 Factorise LHS
Critical values of x: –5 and 5 Make a rough sketch of a parabola
If (***)(***) < 0 (it means where y is negative)
Read off the x values of the graph under the x-axis
(y = ax2 + bx + c ... y is equal to what is defined in terms of x)
Activity 5
Solve for x if
- (x+3)(x – 5) ≤–12
- –x ≤ 2x2 – 3 [10]
Solutions
|
2.8 Simultaneous equations
e.g.19
Solve for x and y simultaneously:
y + 2x – 2 = 0 and 2x² + y² = 3yx
In this example, a quadratic equation and a linear equation must be solved simultaneously. Use the following steps:
Step 1: Use the linear equation to make one of the unknowns the subject of the equation (i.e. get x or y alone on one side of the equation).
Step 2: Substitute x or y (whichever is the subject of the equation) into the quadratic equation. The equation will contain only one unknown.
Step 3: Solve the one unknown.
Step 4: Substitute the solved unknown into the linear equation to solve for the other unknown.
(When you divide, you sometimes need to round off to the closest numbers that are easier to divide.)
| Solution y + 2x – 2 = 0 ………….eqn (1) 2x² + y² = 3yx……………...eqn (2) (Always label the equations: equation 1 (eqn 1) and equation 2 (eqn 2)) Step 1: y + 2x – 2 = 0..............from eqn (1) ∴ y = 2 – 2x................eqn (3) (If the coefficient of y in the linear equation is one, get y alone on one side of the equation. If the coefficient of x in the linear equation is one, get x alone on one side of the equation. This way, you will not have to deal with fractions.) Step 2: Substitute eqn (3) in eqn (2) 2x2 + y2 = 3yx ∴ 2x2 + (2 – 2x) 2 = 3x(2 – 2x) Step 3: 2x2 + (2 – 2x)(2 – 2x) = 3x(2 – 2x) 2x2 + 4 – 8x + 4x2 = 6x – 6x2 12x2 – 14x + 4 = 0 ÷ 2 ∴ 6x2 – 7x + 2 = 0 ∴ (3x – 2)(2x – 1) = 0 ∴ x = 2/3 or x = ½ Step 4: Substitute x = 2/3 in eqn (3) Substitute x = ½ in eqn( 3) |
e.g.20
Given the functions y = 6/x and y = x − 1, find the coordinates of the points of intersection of the two graphs algebraically.
y = 6/x … eqn (1)
y = x – 1 … eqn (2)
Substitute eqn (2) into eqn (1):
(Wherever there is a y, replace it with (x – 1), using brackets)
x − 1 = 6/x
∴ x2 − x = 6 LCD = x
∴ x2 − x − 6 = 0
∴ (x − 3)(x + 2)
∴ x = 3 and x = − 2
Subst. x = 3 in eqn(2): Subst. x = − 2 in eqn(2):
y = 3 − 1 = 2 y = − 2 − 1 = − 3
∴ (3;2) and (− 2; − 3) are the points of intersection
Both these points satisfy the equations.
The graphs of the two equations will intersect at two points.
(In order to determine the points of intersection of two graphs, we solve the equations of the graphs simultaneously.)
Activity 6
Solve the following equations simultaneously.
1. 2x + y = 3 and x2 + y + x = y2
2. y = − 6 − 2 and y = − 3x + 2
x + 1
[14]
Solutions
[14] |
2.9 The nature of the roots
2.9.1 Determine the nature of the roots
The roots of any quadratic equation ax2 + bx + c = 0 can be found by
x = –b ± √b2 – 4ac
2a
- The roots of a quadratic equation are the x-values when the equation is zero.
- The roots are the x-intercepts of the graph.
- When you are asked to ‘determine the nature of the roots of an equation’, you are NOT asked to solve the equation.
(Δ = b2 – 4ac
The value of the Δ determines the nature of the roots)
Summary:
|
The nature of the roots also tells us about the x-intercepts of the graph of the quadratic equation.
Nature of roots Graphs
Δ < 0
Roots are non-real.
There are no x-intercepts.
Δ = 0
Roots are real and equal.
There is only one x-intercept and it is at the turning point of the graph.
Δ > 0
Roots are real and unequal (two roots):
If Δ is a squared rational number, roots are rational.
If Δ is not a squared number, the roots are irrational.
e.g.21
- x = − 6 ± √25
4
Δ = 25 ∴ Δ > 0, so there are two real roots.
We can see that 25 is a perfect square ( √25 = 5)
So the roots will be real, rational and unequal. - x = 4 ± √24
2
Δ = 24 ∴ Δ > 0, so there are two real roots. 24 is not a perfect square( √24 = 4,898979486…)
So the roots will be real, irrational and unequal. - x = − 5 ± √−9
8
Δ = –9 ∴ Δ < 0, so √−9 is non-real. There are no real solutions for x, so the roots are non-real.
e.g. 22
The solutions to a quadratic equation are: x = 5 ± √10 + 2a .
For which values of a will the equation have equal roots.
| Solution The equation will have equal roots if Δ = 0. Δ = 10 + 2a 0 = 10 + 2a 10 = −2a ∴ a = −5 |
Activity 7
- Show that the roots of x2 – 2x – 7 = 0, are irrational, without solving the equation. (3)
- Show that x2 + x + 1 = 0 has no real roots. (3)
- If x = 2 is a root of the equation 3x2 – 5x – 2k = 0, determine the value of k. (2)
- The solutions to a quadratic equation are: x = 5 ± √12 − 3a .
For which value(s) of a will the equation have equal roots. (3) - Determine the value(s) of k for which the equation 3x2 + (k + 2) x + k = 0 has equal roots (4)
[15]
Solutions
|
–3 < 0 ∴ is non-real
32 is not a perfect square so the roots are irrational.
2.9.2 Problem solving using quadratic equations
You can use an equation to represent a problem. Find what part of the problem is unknown and needs to be represented by a variable.
e.g. 23
The area of a rectangle is 12 m2.
The length is 4 metres longer than the breadth. Find the dimensions of the rectangle.
We don’t know the length or the breadth of the rectangle.
We do know that the length is 4 m longer than the breadth.
It makes sense to let the breadth be x metres. Then the length is x + 4 metres.
Draw a picture to help you. Let breadth be x metres
Area of rectangle = length × breadth
12 = (x + 4)x
12 = x2 + 4x
0 = x2 + 4x – 12
0 = (x + 6)(x – 2)
∴ x + 6 = 0 or x – 2 = 0
x = –6 x = 2

Length and breadth must both be positive lengths. You can’t have a negative length!
So x ≠ –6
∴ x = 2 and so the breadth is 2 metres.
The length is x + 4 and so the length is 6 metres.
(m2 here means square metres.
It is not a variable.
Dimensions: the measurements of the sides)
What you need to be able to do:
- Solve quadratic equations by factorising when possible.
- Rewrite a quadratic equation that is written in the general form
y = a x2 + bx + c in the form
y = a(x + p)2 + q by completing the square. - Use completing the square to solve quadratic equations.
- Use the formula x = − b ± √b2 −4ac to determine the roots of an equation.
2a - Use the value of the discriminant ( b2 − 4ac) of a quadratic equation to determine the nature of the roots.
- Solve linear and quadratic inequalities.
- Solve simultaneous equations to find the points of intersection between two different functions.