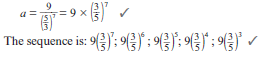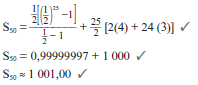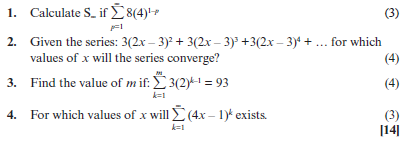NUMBER PATTERNS, SEQUENCES AND SERIES GRADE 12 NOTES - MATHEMATICS STUDY GUIDES

More in this category: « ALGEBRA GRADE 12 NOTES - MATHEMATICS STUDY GUIDES FUNCTIONS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES »
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

 3.1 Number patterns

A list of numbers in order is called a number pattern or number sequence.
We need at least three numbers in the list to work out if the numbers form a pattern. If we only have two numbers, we cannot be sure what the pattern is.
For example, if we have the list 2; 4; … many different number patterns are possible:
The pattern could be 2; 4; 6; … add 2 to each number to get the next number
OR 2; 4; 8; … multiply each number by 2 to get the next number
OR 2; 4; 2; 4; … repeat the pattern
A single number in a pattern or sequence is called a term.
Term 1 is written as T1, term 2 is written as T2 and so on. The number of the term shows its position in the sequence.
T10 is the 10th term in the sequence.
Tn is the nth term in a sequence.

e.g.1

  1. Look at the number pattern 3; 8; 13; …
    1
    If we keep adding 5 to each term we get the next term:
    T4 = 13 + 5 = 18; T5 = 23; T6 = 28, etc.
  2. Look at the number pattern 5; 15; 45; …
    2
    In this pattern, each term is multiplied by 3 to get the next term.
    So T4 = 45 × 3 = 135; T5 = 405; T6 = 1 215, and so on.
  3. Look at the sequence: 1; 4; 9; …
    T1 = 12; T2 = 22; T3 = 32
    These are all perfect square numbers. Each number is the number of the term squared.
    So T4 = (4)2 = 16; T5 = (5)2 = 25; T6 = (6)2 = 36, and so on.

It is important to learn to recognise square numbers.

3.2 Arithmetic sequences

Arithmetic sequence is a sequence where the common difference (d) between consecutive terms is constant.
T2 – T1 = T3 – T2 = Tn – Tn–1 = d (common difference)

e.g 2
Given the sequence: 5; 9; 13; 17 ; . . .

  1. Determine the common difference
  2. Determine the next two terms
Solution
d = 9 – 5 = 13 – 9 = 4
T5 = 17 + 4 = 21 and T6 = 21 + 4 = 25 


If we use a for the first term T1, d for the common difference, then the general term Tn for an arithmetic sequence is: Tn = a + (n – 1)d
e.g. 3
Given the sequence 4; 10; 16; . . .

  1. Determine a formula for the nth term of the sequence.
  2. Calculate the 50th term.
  3. Which term of the sequence is equal to 310

Solutions

  1. a = 4 and d = 10 – 4 = 16 – 10 = 6
    Tn = a + (n – 1) d
    = 4 + (n – 1) 6
    = 4 + 6n – 6
    = 6n – 2
  2. T50 = 6 × 50 – 2
    = 300 – 2
    = 298
  3. 6n – 2 = 310
    6n = 312
    n = 52 

Activity 1

  1. Given the sequence 6; 13; 20; …
    1. Determine a formula for the nth term of the sequence.
    2. Calculate the 21st term of this sequence.
    3. Determine which term of this sequence is 97. (5)
  2. Consider this number pattern: 8; 5; 2; …
    1. Calculate the 15th term.
    2. Determine which term of this sequence is –289. (4)
  3.  
    1. Given the arithmetic sequence 1 − p; 2p − 3; p + 5; . . . determine the value of p.
    2. Determine the values of the first three terms of the sequence. (5)
      [14]

Solutions

  1.  
    1. It is an arithmetic sequence because there is a common difference.
      a = 6; d = 7 Tn = a + (n – 1)d 
      Tn = 6 + (n – 1)(7)
      Tn = 7n – 1 
    2. T21 = 7(21) – 1 = 147 – 1 = 146 
    3. 97 = 7n – 1 
      ∴98 = 7n
      ∴14 = n 
      ∴97 is the 14th term of the sequence. (5)
  2.  
    1. It is an arithmetic sequence: a = 8; d = 5 – 8 = 2 – 5 = – 3
      Tn = a + (n – 1)d
      ∴T15 = 8 + (15 – 1)(–3) 
      T15 = 8 + 14(–3)
      T15 = 8 – 42 = –34 
    2. Tn = a + (n – 1)d
      – 289 = 8 + (n – 1)(–3) 
      ∴– 289 = 8 – 3n +3
      ∴– 300 = –3n
      ∴100 = n 3 ∴– 289 will be the 100th term (4)
  3.  
    1. Since this is an arithmetic sequence, you can assume that there is a common difference between the terms.
      d = T2 – T1 = T3 − T2
      ∴(2p – 3) – (1 – p) = ( p + 5) – (2p – 3) 
      3p – 4 = – p + 8 
      4p = 12
    2. p = 3
      T1 = 1 – p = 1 – 3 = –2
      T2 = 2p – 3 = 2(3) – 3 = 3 
      T3 = p + 5 = 3 + 5 = 8 
      So the first three terms of the sequence are –2; 3; 8 (5)
      [14] 

3.3 Quadratic sequences

At least four numbers are needed to determine whether the sequence is quadratic or not.
Consider this number pattern:
There is no common difference between the numbers.
The differences are 6; 10; 14; 18.
Now we can see if there is a second common difference.
3
In this sequence, there is a second common difference of 4.
The next term will be: T6 = 54 + (18 + 4) = 76
A pattern with a common second difference is called a quadratic number sequence.
The general formula for any term of a quadratic sequence is: Tn = an2 + bn + c
4

If Tn = an2 + bn + c then 2a is the second difference
3a + b is T2 – T1
a + b + c is the first term 

e.g.4
Look at the number sequence 12; 20; 32; 48; . . .

  1. 2nd common difference is 4
    So 2a = 4 ∴a = 2
  2. T2 – T1 = 8
    So 3a + b = 8 ∴ 3(2) + b = 8
    ∴ b = 2
  3. 1st term is 12
    So a + b + c = 12 ∴ 2 + 2 + c = 12
    ∴ c = 8
    ∴Tn = 2n2 + 2n + 8
    ∴T5 = 2(5)2 + 2(5) + 8 = 68
    ∴T6 = 2(6)2 + 2(6) + 8 = 92

5

Activity 2

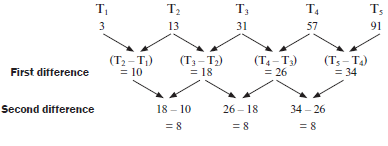
  1. Consider the number pattern: 3; 13; 31; 57; 91; …
    1. Determine the general term for this pattern.
    2. Calculate the 7th term of this pattern.
    3. Which term is equal to 241? (9)
  2. Find term 6 of this pattern and then find the rule in the form
    Tn = an2 + bn + c
    –1 ; 3; 9; 17; 27 ... (4)
    [13]

Solutions

  1.  
    1. It helps to make a diagram:
      6
      ∴ it is a quadratic sequence.
      2a = 8 ∴ a = 4 
      3a + b = 10 ∴3(4) + b = 10
      b = –2 
      a + b + c = 3 ∴ 4 + (–2) + c = 3
      c = 1 
      ∴Tn =4n2 – 2n + 1 
    2. T7 = 4(7)2 – 2(7) + 1 
      = 4(49) – 14 + 1
      = 183 
    3. 241 = 4n2 – 2n + 1
      0 = 4n2 – 2n + 1 – 241 make the equation = 0 to solve
      0 = 4n2 – 2n – 240
      0 = 2n2 – n – 120 divide through by 2
      0 = (2n + 15)(n – 8) 
      factorise
      ∴ 2n + 15 = 0 OR n – 8 = 0
      ∴ n = –7,5 OR n = 8 3 (9) 
  2. T1       T2        T3         T4         T5
       –1      3         9           17       27 ...
              4       6          8          10
                  2         2           2 
    ∴T6 = 27 + (10 + 2) = 39 3 use the pattern of the numbers
    2a = 2 ∴a = 1
    3a + b = 4
    3(1) + b = 4 ∴ b = 1
    a + b + c = –1
    1 + 1 + c = –1 ∴ c = –3
    Tn = n2 + n – 3  (4)
    [13]

n = –7,5 not possible because n is the position of the term so it must be a positive natural number. ✓
∴ 241 is the 8th term of the sequence.

3.4 Geometric sequences

When there is a common ratio (r) between consecutive terms, we can say this is a geometric sequence.
If the first term (T1) is a, the common ratio is r, and the general term is Tn, then:

r =T2 = T3  =  Tn  
     T1   T2     Tn-1
and = Tn = arn-1 

Look at the sequence 5; 15; 45; 135; 405; …
15 = 3  45 = 3 and 135 = 3 and so the common ratio is 3.
 5         15               45
Therefore the sequence is geometric. To get the next term you multiply the preceding term by the common ratio.
(Given the sequence, check whether it is arithmetic, geometric or quadratic.)

e.g.5
Given the sequence 1; 2/3 ; 4/9 ; ...

  1. Determine the next two terms
  2. Which term of the sequence is equal to  32  ?
                                                                   243

7

e.g. 6
In a geometric sequence, the fifth term is 80 and the common ratio is –2.
Determine the first three terms of the sequence.
T5 = 80 and r = –2
T5 = ar4 = a(–2)4 = 80
16a = 80
a = 5
∴T1 = 5; T2 = 5(–2)1 = –10; T3 = 5(–2)2 = 20

Activity 3

  1. Determine the 10th term of the sequence: 3; 6; 12; . . . (2)
  2. Determine the number of terms in the sequence: 2; 4; 8; . . .; 1024 (2)
  3. If 5; x; 45 are the first three terms of a geometric sequence, determine the value of x. (2)
  4. Determine the geometric sequence whose 8th term is 9 and whose 10th term is 25. (3)
    [9]

Solutions

  1. a = 3; r = 6/3 = 12/6 = 2              
    Tn = arn−1
    T10 = 3(2)10−1 = 3(2)9 = 3 × 512 = 1536 (2)
  2. a = 2; r = 4/2= 8/4 = 2
    arn–1 = 1024
    2(2)n–1 = 210 = 2n = 210 
    ∴ n = 10 (2)
  3. x/5 = 45/x
    x = ± √225 = ± 15 (2)
  4. ar7 = 9
    ar9 = 25
    ar9 = 25 
    ar7     9
    ∴r2 = 25/9
    r = 5/3
    8
    [9] 

3.5 Arithmetic and geometric series

When we add the terms of a sequence together, we form a series.
We use the symbol Sn to show the sum of the first n terms of a series.
So Sn = T1 + T2 + T3 + T4 + … + Tn
3.5.1 Arithmetic series

The formula is Sn = n/2[2a + (n − 1)d] where Sn is the sum of n terms,
a is the first term,
n is the number of terms and
d is the common difference. 


Proof

The general term of an arithmetic series is Tn = a + (n – 1)d
So Sn = T1 + T2 + T3 + T4 + … + Tn
Sn = a + [a + d] + a + 2d + … + [a + (n – 2)d] + [a + (n – 1)d] … equation 1
If we write the series in reverse we get:
Sn = [a + (n – 1)d] + [a + (n – 2)d] + [a + (n – 3)d] + … + [a + d] + a … equation 2
We can add equation 1 and equation 2.
So 2Sn = [2a + (n – 1)d] + [2a + (n – 1)d] + [2a + (n – 1)d] + … +
[2a + (n – 1)d] + [2a + (n – 1)d]
2Sn = n [2a + (n – 1)d]
Sn = n/2 [2a + (n – 1)d] 

This formula is provided on the information sheet in the final exam.

Add first terms: a + [a + (n – 1)d]
= 2a + (n – 1)d
Add second terms: a + d + [a + (n – 2)d]
= 2a + (n – 1)d
Add third terms: a + 2d + [a + (n – 3)d]
= 2a + (n – 1)d
Add last terms: [a + (n – 1)d] + a
= 2a + (n – 1)d
i.e (a + l), n times

Alternative Proof

Or Sn = a + [a + d] + [a + 2d] + … + [l – d] + l … equation 1
In reverse Sn = [a + (n – 1)d] + [a + (n – 2)d] + [a + (n – 3)d] + … + [a + d] + a
Sn = l + [l – d] + [l – 2d] + . . . + [a + d] + a … equation 2
Adding equation 1 and equation 2
2Sn = [a + l] + [a + l] + . . . + [a + l] n times
2Sn = n[a + l]
∴Sn = n/2 [a + l] 

e.g. 7

  1. Determine the sum of the first 20 terms of the series:
    3 + 7 + 11 + 15 + …
  2. The sum of the series 5 + 3 + 1 + . . . is –216, determine the number of terms in the series

Solutions

  1. a = 3, n = 20, d = 4
    Sn = n/2 [2a + (n – 1)d]
    S20 = 20/2 [2(3) + (19)4]
    S20= 10(6 + 76)
    S20 = 820
    The sum of the first 20 terms is 820
  2. a = 5 d = –2 Sn = –216 Sn = n/2 [2a + (n – 1)d] n = ?
    Substitute into the formula:
    –216 = n/2 [2(5) + (n – 1)(–2)]
    –216 = n/2 [10 + –2n + 2]
    –216 = n/2 [12 – 2n]
    –432 = 12n – 2n2
    –432 = –2n2 + 12n …. Make equation = 0
    2n2 – 12n – 432 = 0 …. Divide through by 2 (common factor)
    n2 – 6n – 216 = 0 …. Factorise trinomial
    (n – 18)(n + 12) = 0
    ∴ n – 18 = 0 or n + 12 = 0
    n = 18 or n = –12
    n > 0 ∴n = 18
    ∴18 terms of the series add up to –216. 

Activity 4

  1. Determine the sum of the series: 19 + 22 + 25 + . . . + 121 (3)
  2. The sum of the series 22 + 28 + 34 + . . . is 1870. Determine the number of terms. (2)
  3. Given the arithmetic sequence -3; 1; 5; …,393
    1. Determine a formula for the nth term of the sequence.
    2. Write down the 4th, 5th, 6th and 7th terms of the sequence.
    3. Write down the remainders when each of the first seven terms of the sequence is divided by 3.
    4. Calculate the sum of the terms in the arithmetic sequence that are divisible by 3. (10)
  4. The sum of n terms is given by Sn  = n/2 (1 + n) . Determine T5. (3)
  5. 3x + 1; 2x; 3x − 7 are the first three terms of an arithmetic sequence. Calculate the value of x. (3)
  6. The first and second terms of an arithmetic sequence are 10 and 6 respectively.
    1. Calculate the 11th term of the sequence.
    2. The sum of the first n terms of this sequence is –560. Calculate n. (6)
      [27]

Solutions

  1. a = 19 and d = 3
    Tn = 3n + 16 = 121
    3n = 105
    n = 35
    Sn  = n/2(a + l)
    S35  = 35/2 (19 + 121) =  35/2 (140) = 35 × 70 = 2450 (3)
  2. a = 22 and d = 6
    Sn  =  n/2 [2a + (n − 1)d] n
    n/2 [2 × 22 + (n − 1)6] = 1870
    19n + 3n2  = 1870
    3n2  + 19n − 1870 = 0
    (3n + 85)(n − 22) = 0 3
     ∴ n = 22
    n cannot be a negative because it is the number of terms (2)
  3.  
    1. Tn = –3 + (n − 1)4 
      4n – 7 = Tn 
    2. T4  = 5 + 4 = 9; T5  = 9 + 4 = 13; 3 T6  = 13 + 4 = 17 and
      T7  = 17 + 4 = 21 
    3. 0; 1; 2; 0; 1; 2; 0
    4. Tn = –3 + 12 (n − 1)
      393 = 12n – 15
      12n = 393 + 15 = 408 
      n = 34
      S34  = 34/2 × (–3 + 393)
       = 17 × 390
       = 6630 (10)
  4. S5  = 5/2 ( 1 + 5 )  = 15 
    S4  = 4/2 ( 1+ 4 )  = 10 
    T5 = 15 – 10 = 5 (3)
  5. T2 – T1 = T3 – T2
    2x – (3x + 1) = (3x – 7) – 2x 
    2x – 3x – 1 = 3x – 7 – 2x
    –2x + 6 = 0 
    2x = 6
    x = 3  (3)
  6.  
    1. Tn = a + (n – 1)d
      T11 = 10 + (11 – 1)(–4) 
      = –30 
    2. Sn =n/2 [2a + (n – 1)d]
      –560 = n/2 [2(10) + (n – 1)(–4)] 
      –1120 = –4n2 + 24n
      4n2 – 24n – 1120 = 0
      n2 – 6n – 280 = 0 
      (n – 20)(n + 14) = 0 
      n = 20 or n = –14
      n = 20 only because number of terms cannot be a negative number (6)
      [27] 

3.5.2 Geometric series

The formula is Sn  = ​ ​ a( rn  − 1) for r > 1 or Sn  = ​ ​ a(1 −  rn) for r < 1
                                       r - 1                                     r - 1
where a is the first term
r is the common ratio
n is the number of terms
Sn is the sum of the terms

Proof:

The general term of a geometric series is Tn = arn – 1
So Sn = T1 + T2 + T3 + T4 + … + Tn
Sn = a + ar + ar2 + … + arn–2 + arn–1
rSn = ar + ar2 + ar3 + … + arn–1 + arn
    Sn = a + ar + ar2 + … + arn–2 + arn–1      
 rSn – Sn = –a + 0 + 0 + … + 0 + 0 + arn
multiply each term by r write down the series again with like terms under each other
∴ rSn – Sn = arn – a  subtract each bottom term from each top term
Sn(r – 1) = a(rn – 1)   Sn and a are common factors 
So Sn =a(rn –1)  Divide through by (r – 1)
                 r - 1
We can also use for Sn = a(1 – rn) for r < 1
                                            1 - r

The proof must be learnt for exams

e.g. 8
Evaluate: 25 + 50 + 100 + … to 6 terms

Solution
We need to check if this is an arithmetic series or a geometric series first.
You should see that there is a common ratio of 2 because 50/2 = 2 and 100/50 = 2
r = 2
∴ It is a geometric series and a = 25, n = 6, r = 2
Sn = a(1 – rn)
            1 - r
S6 = 25(1 – 26) 26 = 64
              1 - 2
S6 = 25(1 – 64)
              - 1
S6 = 25(–63)
            - 1
= 1 575 

So the sum of the first 6 terms of the series is 1 575.

Activity 5

  1. Determine 3 + 6 + 12 + 24 + . . . to 10 terms (2)
  2. If 2 + 6 + 18 + . . . = 728, determine the value of n. (3)
    [5]

Solutions

  1. a = 3 and r = 6/3 =  12/6  = 2
    Sn =  a( r n  − 1)
                  r - 1
    S10 = 3( 2 10  − 1) = 3(1024 − 1) = 3069 (2)
                    2 - 1
  2. a = 2 and r = 6/2  = 18/6 = 3
    Sn =  2(3n  − 1) = 728 
                  3 - 1
    2(3n  − 1)  = 728
          2
    3n − 1 = 728
    3n = 729 = 36 
    ∴ n = 6 (3)
    [5] 

3.5.3 Sigma notation
Here is another useful way of representing a series.
The sum of a series can be written in sigma notation.
The symbol sigma is a Greek letter that stands for ‘the sum of’.
9

To determine the number of terms: top value minus bottom value plus 1 i.e the number of terms in this case is (17 – 3 ) +1 = 15
e.g. 9

15
Activity 6
10
Look for two different sequences in the pattern and separate them

Solutions

  1. The question asks you to find the sum of the terms from n = 4 to
    n = 70 if the nth term is 2n – 4.
    a = T1 = 2(4) – 4 = 4 Find the first term a
    T2 = 2(5) – 4 = 6
    T3 = 2(6) – 4 = 8
    So the sequence is 4; 6; 8; … and this is an arithmetic series. 
    To check d, calculate T2 – T1
    d = T2 – T1 = 6 – 4 = 2
    n = (70 – 4) + 1 = 67 There are 67 terms
    Now we can substitute these values into the formula to find the sum of 67 terms.
    Sn = n/2 [2a + (n – 1)d]
    S67 = 67/2 [2(4) + (67 – 1)2]
    S67 = 33.5 [8 + 132] = 4690
    11
    (3)
  2. This is a geometric series because 5(3)k–1 has the form ark–1, T1 = 5(3)1–1 = 5 ;
    T2 = 5(3)2–1 = 15; T3 = 5(3)3–1 = 45
    a = 5; r = 3; n = m and Sm  =  65
    Sn = a( rn −1)… substitute
                r - 1
    65 = 5(3m  − 1) … multiply through by 2
                  2
    65 = 5(3m  − 1)
                    2
    130 = 5.3m – 5 … add like terms
    135 = 5.3m … divide through by 5
    27 = 3m … write 27 as a power of 3
    33 = 3m … bases are the same, so the powers are equal
    ∴ m = 3 (4)
  3.  
    1. T1, T3 and T5 form a sequence with a common ratio of ½, so T7 is 1/16 . 
      T2, T4 and T6 form a sequence with a common difference of 3, so T8 is 13.
    2. S50 = 25 terms of 1st sequence + 25 terms of 2nd sequence
      S50 = ( ½ + ¼ + 1/8 + … to 25 terms) + (4 + 7 + 10 + 13 + … to 25 terms) 
      12

(5)
[12] 

3.5.4 Infinite geometric series
An infinite series is one in which there is no last term, i.e. the series goes on without ending.

e.g.10
6 + 3 +  3/2 + 3/4 + ...

13
The terms of this series are all positive numbers and the sum will get bigger and bigger without any end. This is called a divergent series.

e.g. 11
Look at this infinite series:
S∞ =  1 + ½ + ¼ + 1/8 + 1/16 + ....
S2 = 1 + ½ = 1 ½ = 1.5
S3 = 1 ½ + ¼ = 13/4 = 1.75
S4 = 13/4 + 1/8  = 17/8 = 1.675
S5 = 17/8 + 11/16 = 115/16 = …..
This series will converge to 2. It is therefore called a convergent series and we can write the sum to infinity equals 2: S∞ = 2
You can identify a convergent infinite series by looking at the value r
An infinite series is convergent if – 1  <  r  <  1 , r  ≠  0

The formula for the sum of a convergent infinite series:
S∞ =   a   
        1 - r
where a is the first term, r is the common ratio
This formula is provided on the information sheet in the final exam. 

e.g. 12

  1. Look again at the example where S∞  =  1 + ½ + ¼ + 1/8 + 1/16 + ....
    a = 1 and r = ½ 0 < r < 1
    S∞ =   a   
            1 - r
    S∞ =   1    = 1 ÷ ½ 
            1 - ½ 
    S∞ =  1 × 2 = 2
  2. For which value(s) of x will 8x2 + 4x3 + 2x4 + … be convergent?
    For convergent geometric series, –1  <  r  <  1
    r = T2 ÷ T1
    = 4x3 ÷ 8x2
    = x/2
    ∴ –1 < x/2 < 1 multiply through by 2
    –2 < x < 2…………………..x ≠ 0

Activity 7
14

Solutions

  1. T1 = 8(4)1 – 1 = 8 = a
    To find r, find the common ratio using T1 and T2, T2 and T3.
    T2 = 8(4)1 – 2 = 8(4)–1 = 8 × ¼ = 2
    T3 = 8(4)1 – 3 = 8(4)–2 = 8 × 1/16 = ½
    T2 ÷ T1 = 2/8 =  ¼  and T3 ÷ T2 =½ = ½ x ½ = ¼
                                                         2
    so r = ¼ and a = 8
    ∴S∞ =   a     =    8    =  8 
               1 - r      1 - ¼    3/4
    = 8 x 4/3 = 32/3
    When dividing by a fraction, you can multiply by the inverse
    ∴S∞ = 32/3 or 102/3 (3)
  2. This is a geometric series with r = 2x – 3 
    To converge –1  <  r  <  1 
    –1  <  2x – 3  <  1 Add 3 to both sides
    2 < 2x < 4 Divide by 2 on both sides
    1 < x < 2 3 x ≠ 3/2 (4)
    The series will converge for 1 < x < 2
  3. a = 3; r = 2; Sm = 93
    Sn  =  a(1 −  r n )
                  1 - r
    93 = 3 (1 − 2m )
                1 - 2
    93 = 3( 1 − 2m)
                - 1
    –93 = 3(1 – 2m) 
    –31 = 1 – 2m
    2m = 32
    2m = 2 5
    ∴ m = 5 (4)
  4. r = 4x – 1 
    –1 < r < 1
    -1 < 4x -1 < 1; x ≠ ¼
    0 < 4x < 2
    0 < x < ½ (3)
    [14] 

What you need to be able to do:

  • Find the next few terms in a given sequence.
  • Identify arithmetic sequences, quadratic sequences and geometric sequences
  • Apply knowledge of sequences and series to solve real life problems
  • Find the first difference and the second common difference in a quadratic sequence.
  • Find the general terms of sequences.
  • Know how to derive the formulae for the sum of Arithmetic or Geometric Series.
  • Solve problems using these sum formulae.
  • Work with the sum of infinite geometric sequences that are convergent.
Last modified on Wednesday, 08 September 2021 11:56
Published in Grade 12 Mathematics Study Guide and Notes

Related items

More in this category: « ALGEBRA GRADE 12 NOTES - MATHEMATICS STUDY GUIDES FUNCTIONS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES »
back to top