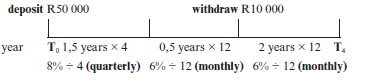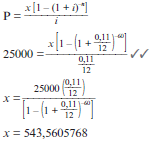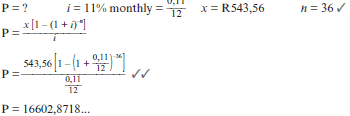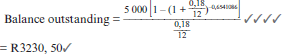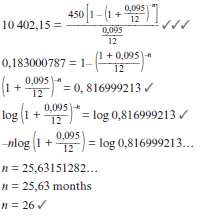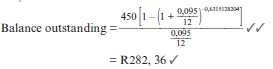FINANCE GROWTH AND DECAY GRADE 12 NOTES - MATHEMATICS STUDY GUIDES

More in this category: « TRIG FUNCTIONS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES CALCULUS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES »
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

6.1 Revision: Simple and compound interest

Financial terms

  • Interest is a fee paid for the use of borrowed money, or money earned on money saved. It is calculated as a percentage of the money borrowed or lent.
  • Simple interest is the interest on an initial (principal) sum of money. Each year you receive or you are charged the same amount of interest.

e.g 1
Simple interest of 6% p.a. (per year) on R100 means that if you borrow R100 for a year, you owe that R100 and another R6 back. So you owe R106.
If you borrow R100 for 2 years, you will owe R100 + R6 + R6 = R112.
Micro-lenders and Hire Purchase agreements often work on simple interest at a monthly or at a yearly interest rate.
Percentage increase or decrease in populations, number of learners etc., can also be calculated using simple interest formula.

  • Compound interest is also interest on a principal amount P. For each year, the previous year’s final amount becomes the new principal amount. So the
    interest is calculated on the principal and the interest from the previous year.
    Compound interest of 6% p.a. (per year) on R100 means that if you borrow
    R100 for 2 years, you owe R100 + R6 = R106 in the first year.
    In the second year, you owe R106 + 6% of R106.
    R106 + (6% × R106) = R106 + R6,36 = R112,36
    Here are the formulae for simple and compound interest.

Simple interest: A = P(1 + ni)
where P is the principal (original sum of money invested or borrowed)
i is the interest rate
n is the number of years
A is the final amount
In all calculations, round off your final answer only.

Compound interest: A = P(1 +i)n
where P is the principal (original sum of money invested or borrowed)
i is the interest rate
n is the number of years
A is the final amount

e.g.2
If you borrow R300 at 9% p.a simple interest, how much will you owe after 7 years?

Solution
A = ?
P = R300
i = 9% = 9/100 = 0,09
n = 7 years
A = P(1 + ni)
A = 300(1 + 7 × 0,09) = 489
After 9 years you will owe R489.

  • Write down what is given.
  • Decide what you need to find.
  • Solve for that variable.

If you borrow R300 at 9% p.a compound interest, how much will you owe after 7 years?
A = ?
P = 300
i = 9% = 9/100 = 0,09
n = 7 years
A = P(1 + i) n
A = 300(1 + 0,09) 7
A = 300(1,09) 7
A = 548,411736…
A ≈ R548,41 to the nearest cent.
Which is the better option?
R548,41 – R489 = R59,41
So compound interest is R59,41 more than simple interest after 7 years.

e.g.3

  1. You invest R1 570 at 11% p.a. compounded monthly.
    1. How much will you receive after 7 years?
    2. How much interest have you earned after 7 years?

Solutions

    1. A = P(1 + i)n
      A = ? P = R1 570 n = 7 years × 12 months = 84 time periods
      (Compounded monthly means the interest is calculated at the end of every month. So convert years to months.)
      i = 11% ÷ 12 months =0,11/12
      A = 1570 (1 + 0.11/12)7 x 12
      (11% per annum compounded monthly, so we divide the interest rate by 12 months.)
      A = 3 378,959672…
      You will receive R3 378,96 (to the nearest cent) after 7 years.
    2. You have earned R3 378,96 – R1 570 = R1 808,96 interest 

 

Interest per annum compounded:
monthly ➞  i  
                 12
n years × 12 months
quarterly ➞ i 
                   4
n years × 4 quarters in the year
semi-annually or half-yearly, (every 6 months) ➞ i  n years × 2
                                                                              2 


Activity 1
6.1.1 You invest R1 700 at an interest rate of 10% compounded quarterly. Calculate how much your investment is worth after 6 years. (3)
6.1.2 R25 000 is invested into a savings account. Calculate the value of the investment of the savings after 5 years if interest rates are:

  1. 11% compounded monthly
  2. 11% compounded semi-annually (5)
    [8]

Solutions
6.1.1 A = ? P = R1 700 n = 6 years × 4 = 24
i = 10% compounded quarterly
so divide by 4 i = 0,10
                              4
A = P(1 +i)n
A = 1 700 ( 1  +  0,10/4)24
= R3 074,83 (to nearest cent) (3)
6.1.2

  1. A = R25 000 i = 0,11 n = 5 × 12
                              12
    A = 25 000 ( 1 + 0,11)5 × 12
                                12
    = R43 222,89 
  2. A = R25 000 i = 0,11 n = 5 × 2
                                2
    A = 25 000 ( 1 + 0,11)5 × 2
                                2
    = R42 703,61 (5)
    [8] 

6.2 Calculating the value of P, i and n

We can also use the formulae for compound and simple interest to calculate the principal P, the rate of interest i, or the time period n.

e.g.4
1. How much must John invest now so that after 5 years at 8% simple interest, he will have R4 200?

Solution
1. A = R4 200
n = 5
i = 8%
P = ?
A = P(1 + n.i)
4 200 = P(1 +5(0,08))
4 200 = P(1,4)
P = 4 200 = 3 000
        1,4 
∴ John must invest R3 000.


e.g. 5 (finding i)
A population increases from 12 000 to 214 000 in 10 years. At what annual (compound) rate does the population grow? (Give your answer correct to one decimal place.)

Solution
A = 214 000 P = 12 000 n = 10 i = ?
A = P(1 + i)n
214000 = 12000(1 + i)10
214000 = (1 + i)10
12000
10√214000 = 1 + i
      12000
1,333899939… –1 = i
0,333899939... = i
∴ i = 33,389..%
The population grew at an annual (compound) rate of 33,4% (correct to
one decimal place). 

e.g.6 (finding n)
Ms Gumede puts R3 500 into a savings account which pays 7,5% p.a. compound interest. After some years, her account is worth R4 044,69.
For how long did she invest the money?

Solution
A = R4 044,69
P = R3 500
n = ?
i = 7,5% p.a. = 0,075
A = P(1 +i)n
4 044,69 = 3 500(1 +0,075)n
4 044,69 = 3 500(1,075)n
4044,69 = (1,075)n
  3500   
1,155625714 = (1,075)n
n = log1,075 1,155625714
n = 2,000008543
n = 2 years 
So Ms Gumede invested the money for 2 years.
  • Substitute for A, P and i
  • Simplify
  • Divide by 3500
  • Write in logarithmic form
  • Use the log keys on the calculator
  • Round off the answer to the nearest year

Activity 2

  1. Mary borrowed a certain sum of money from a bank at a compound interest rate of 15% calculated quarterly. After 3 years she now owes R7 000. How much did she borrow? (3)
  2. R1 570 is invested at 12% p.a. compound interest. After how many years will the investment be worth R23 000? (4)
  3. R2 000 was invested in a fund paying interest compounded monthly.
    After 18 months the value of the fund was R2 860, 00. Calculate the interest rate. (4)
    [11]

Solutions

  1. A = R7000
    i = 0.15
           4
    n =3 × 4
    P =?
    7000 = P( 1  + 0,15)3×4 
                             4
    7000 = P(1,555454331) ………… Divide both sides by 1,555454331
    P = R4500,29 (3)
  2. A = P (1 + i)n substitute for A, P and i
    23 000 = 1 570(1 + 0,12)n simplify and divide
    23000 = (1,12)n keep the number on your calculator without rounding
    1570
    14,6496… = (1,12)n use log laws
    n = log1,12 14,6496… Use the log keys on your calculator.
    n = 23,69 years n ≈ 24 years to the nearest year(4)
  3. A = 2860
    P = 2000
    i = ?
    n = 18
    A = P (1 + i)n
    2000( 1  + i )18 = 2860
                   12
    ( 1  + i )18 = 2860
           12        2000
    1 +  i = 18√1.43
         12
      i    = 0,020069541
    12
    i = 0,020069541... 
    i =0,2408344924 × 100
    i = 24,08% (4)
    [11] 

6.3 Simple and compound decay formulae

Decay or depreciation is when a quantity decreases by a percentage of the amount present. For example, your assets (house, car) and machinery lose value through age and use.
Ways of calculating depreciation.
Simple decay or depreciation: A = P(1 –ni)
This is also called straight line depreciation because it can be represented with a straight line graph.

e.g.7
A car worth R120 000 depreciates at a rate of 12% (simple interest) p.a.
How much will the car be worth after 5 years?

Solution:
A = P(1 – ni)
A = ?
P = 120 000 i = 12% = 0,12
n = 5 years
A = 120 000 (1 – 5 × 0,12)
A = 48 000
The car will be worth R48 000 after 5 years. 

Compound decay or depreciation: A = P(1 – i)n
This is also called depreciation on a reducing balance because the interest is calculated on the amount left over as it decreases. The amount left over is ‘the reducing balance’.

e.g.8
A car worth R120 000 depreciates at a rate of 12% p.a. (on a reducing balance).
How much will the car be worth after 5 years?

Solution
A = P (1 – i)n
A = ?
P = 120 000
i = 12% = 0,12
n = 5 years
A = 120 000 (1 – 0,12)5
A = 63 327,83002…
A = R63 327,83 (to the nearest cent)
***Compare this with simple depreciation:
The car’s value is R63 327,83 – R48 000 = R15 327,83 less on simple decay
than on compound decay. 


Activity 3
The value of a piece of machinery depreciates from R10 000 to R 5 000 in 4 years. What is the rate of depreciation, correct to two decimal places, if calculated on the:

  1. Straight line method (i.e. simple depreciation) (3)
  2. Reducing balance (i.e. compound depreciation) (3)
    [6]

Solutions

  1. A = 5 000 P = 10 000 n = 4
    i =? Note: A is less than P
    Straight line method:
    A = P(1 – ni)
    5 000 = 10 000 (1 – 4i) 
     5000  = (1 − 4i) 
    10000
    0,5 – 1 = – 4i
    -0,5 = i
     -4
    0,125 = i
    i =12,5% (3)
  2. Reducing balance:
    A = P (1 – i)n
    5 000 = 10 000(1 – i)4 
     5000  = (1 − i)4
    10000
    0,5 = (1 – i)4
    4√0,5 = 1 – i
    i = 1 – 0,8408…
    i = 0,1591035…
    i = 15,9% (3)
    [6] 

6.4 Nominal and effective interest rates

  1. A nominal interest rate is the quoted interest rate.
  2. An effective interest rate is the actual interest rate received.
    If you are quoted a nominal interest rate of 8% p.a., the resulting effective rate will be different depending on if it is worked out annually, monthly or semi-annually
  3. We use the following formula to calculate the effective interest rate from the nominal interest rate or vice versa:

1 + ieffective = ( 1 + inominal/k)
If k is the number of times per year the interest is calculated.

e.g.9

  1. You borrow R500 at 8% p.a. compounded for one year.
    At the end of the year you owe 500(1+ 0,08)1 = R 540
  2. You borrow R500 at 8% p.a. compounded monthly for one year
    At the end of the year you owe 500 ( 1 + 0,08)1×12
                                                                       12
    = R541,50
    So effectively, you are charged R41,50 interest on R500.
    Your interest rate is actually R41,50 × 100 = 8,3% .
                                                   R500       1
    So the effective interest rate is 8,3% p.a. but the nominal interest rate is 8% p.a.
  3. What is the effective interest rate if 7,5% p.a. is calculated monthly?
Solution
1 + ieffective = ( 1 + 0,075)12
                                12
1 + ieffective =1,07763
ieff = 0,07763
∴ ieff = 7,76% 

Activity 4

  1. Khosi wants to invest R5 000 for 3 years. Which is the better investment for her if the interest is 10,5% p.a compounded quarterly or 10,5% p.a. compounded monthly? (7)
  2. Convert a nominal interest rate of 9% per annum compounded semi-annually to the effective annual interest rate. (2)
    [9]

Solutions

  1. First option: A = ? P = R5 000 i = 0,105  n = 3 × 4
                                                            4
    A = P (1 + i)n
    A = 5 000 ( 1 + 0,105)3×4 Use a calculator to work out the whole answer.
                                4
    A = R6823,51
    Second option: A = ? P = R5 000 i = 0,105  n = 3 × 12
                                                                12
    A = P (1 + i)n
    A = 5000 ( 1 +  0,105)3 x 12 Use a calculator to work out the whole answer.
                              12
    A = R6 841,923
    ∴10,5% compounded monthly gives Khosi a better interest on her investment. (7)
  2. 1 + ieffective = ( 1 + inominal)k k if k is the number of times per year the interest is calculated.
                                          2
    1 + i = ( 1 +  0,09)2
                          2
    1 + i =1,092025 …
    i = 0,092025
    ∴ 9,20% is the effective annual interest rate. (2)
    [9] 

6.5 Investments with time and interest rate changes

Calculations of more than one interest, deposits and withdrawals are best done using timeline.

e.g.10
Thabo invested R 1 000 in a bank for 10 years. The interest rate was 6,5% compounded quarterly for the first 3 years. For the next 5 years, the interest was calculated at 7,2% compounded monthly and for the remainder of the investment, the interest was at 7,8% compounded semi-annually.
How much money would Thabo get at the end of the investment?

Solution
First draw a timeline so that you understand the question.
Over 10 years, the interest rates are different over different time periods.
R1000
1

This can all be worked out in one calculation or you can do separate
calculations. Remember not to round off answers until the end so that
you can have accurate answers.
METHOD 1
A = 1000( 1 + 0.065)3×4 ( 1+ 0.072)5×12 ( 1+ 0,078)2×2
                          4                     12                      2
= R2024,64

METHOD 2
Time1: A = 1000 (1 + 0,065)3×4
                                     4
= R1 213,407579
This amount of R1 213,407579 becomes P for the next calculation
Time2: A = 1213,407579 ( 1 + 0,072)5×12 = R1 737,342911
                                                 12
This amount of R1 735,911122 becomes P for the next calculation
Time3:A = 1 737,342911 ( 1 + 0,078)2×2 
                                                    2
= R2 024,64
After 10 years Thabo will get R 2 024,64 (to the nearest cent) 
NOTE: Rounding off was done on the final answer only. [8] 

Activity 5
Mr. Sithole invests R50 000 in an account which offers 8% p.a. interest compounded quarterly for the first 18 months. The interest then changes to 6% p.a. compounded monthly. Two years after the money is invested, R10 000 is withdrawn. How much will be in the account after 4 years?
[5]

Solution
Draw a timeline. The total length of time is 4 years.
2
METHOD 1
DEPOSIT for the period of 4 years
A = 50000 ( 1 + 0.08)1.5×4 ( 1 +  0.06)2.5×12  − 10000 (1 +  0.06)2×12
                           4                        12                                    12
=R54 124,66 

OR
METHOD 2

First 18 months (18 =1,5 years):
                           12
P = R50 000 i = 8% compounded quarterly = 0,08 n = 1,5 years × 4
                                                                          4
A = 50000 ( 1 + 0,08)1,5×4 = R56 308,12096
                           4
Next 6 months (0,5 years):
P = R56 308,12096 i = 6% compounded monthly = 0,06 n = 0,5 × 12
                                                                                   12
A = 56308,12096 ( 1 + 0,06)0,5×12 
                                      12
= R58 018,62143
R10 000 withdrawn, so R48 018,62143 remains as the new P value.
Next 2 years
P = 48 018,62134 i = 6% compounded monthly = 0,06 n = 2 × 12
                                                                                 12
A = 48018,62134 ( 1 + 0,06)2×12
= R54 124,66 [5] 

Deposit of 50 000 with two different interest for the whole period minus the withdrawal with interest for the remaining period

6.6 Annuities

Annuities are number of equal payments made at regular intervals and subject to a rate of interest.
Types of annuities are: Future value annuities and Present value annuities.
6.6.1 Using the Future Value formula

  • You can save money by putting away the same amount of money every month for use in the future. This can be done through an annuity fund, a retirement fund, a savings account, or a sinking fund. Compound interest is earned on your savings, so you will receive, at some time in the future, the total of all your monthly installments, as well as interest calculated every month on an increasing monthly balance.

Future value formula
When you pay equal monthly installments in order to save money for the future, you can calculate using the future value formula.
F =  x[(1 + i)n  − 1]
                 i
where F is the total accumulated at the end of the time period
x is the monthly installment
i is the interest rate per annum
n is the number of installments/payments
This formula is provided on the information sheet in the final exam.
NOTE: The formula assumes that payments start at the end of the first month.

e.g.11
Sipho plans to save a fixed amount from his salary each month. He starts at the end of the month of his first salary. The bank offers an interest rate of 4,7% p.a. compounded monthly.

  1. Determine the amount he has to save every month if he wants to have R30 000 in his savings account at the end of 4 years.
  2. What is the total amount of interest he will receive after 4 years?

Solutions

  1. Sipho is saving for the future so use the Future Value formula.
    F = R30 000 x is the monthly installment
    i = 4,7% compounded monthly = 0,047 n = 4 × 12 = 48 months
                                                           12
    F = x [(1 + i) n  − 1]
                     i
    30000 = x [ ( 1 + 0,047/12)48 − 1 ]
                              0,047
                                12
    30000 × 0,047/12 = x [ (1  + 0,047/12)48 − 1 ]
    x = 30000 × 0,047/12
    [ ( 1 + 0,047/12)48  − 1 ]
    x = 569,30932...
  2. He must save R569,31 every month for 4 years.
    He will have paid R569,31 × 48 months = R27 326,88
    So the total interest he will receive after 4 years is
    R30 000 – R27 326,88 = R2 673,12

6.6.2 Sinking fund

e.g.12
A printing company buys new printers at a cost of R3,2 million. [Give all answers to the closest rand.]

  1. Calculate the book value of their printers after 5 years, if the depreciation is calculated at 16% p.a. on a reducing balance.
  2. Calculate the cost of replacing the printers at the end of 5 years, if the price of new printers increases by 8,5% p.a.
  3. How much more money would the company need if they sell the old printers at their book value and the money received is used towards the purchase of the new equipment?
  4. The company sets up a fund to make provision for replacing the old equipment at the end of 5 years. They deposit R240 000 at the end of the 1st year, R370 000 at the end of the 2nd year, R420 000 at the end of the 3rd year and R500 000 at the end of the 4th year.
    Determine the total amount of money accumulated in the fund at the end of 5 years if the interest paid on money in the fund is 11,5% p.a. compounded annually.
  5. How much additional money will they need to buy the replacement printers at the end of the replacement period?

Solutions:

  1. P = R3 200 000 i = 16% = 0,16 n = 5
    A = P (1 – i)n
    A = 3 200 000 (1 – 0,16)5
    A = R1 338 278
    Book value of R1 338 278
  2. P = R3 200 000 i = 8,5% = 0,085 n = 5
    A = P (1 + i)n
    A = 3 200 000 (1 + 0,085)5
    A = R4 811 701
    Cost of replacing printers
  3. 4 811 701 – 1 338 278 = R3 473 423
    They need R3 473 423
  4. timeline
    3
    End of year 2:
    P = R240 000 i = 11,5% p.a. = 0,115 n = 1
    A = P (1 + i)n
    A = 240 000 (1 + 0,115)1 = R267600
    R267600+ R370000 = R637600
    End of year 3:
    A = 637600 (1 + 0,115)1 = R710924
    R710 924 + R420 000 = R1130 924
    End of year 4:
    A = R1130 924 (1 + 0,115)1 = R1260980,26
    R1260980,26 + 500 000 = R1760980,26
    End of year 5:
    A = 1760980,26 (1 + 0,115)1 = R1963492,99
    After 5 years, they have R1963492,99 in the fund.
  5. R4 811 701 – R1963492,99 – R1338278 = R1509930,01 still needed for new printers. 


Activity 6: Interpret a graph
1. Ntsako invests R50 000 at 14% p.a. compounded annually. Liz saves R50 000 at 13,7% p.a. compounded monthly.

  1. Who has the most money at the end of 20 years?
  2. Calculate the difference in their investments after 20 years.
    [6]

Solutions

    1. Ntsako: A = 50 000(1 + 0,14) 20 = R687 174,49
      Liz: A = 50000 ( 1 +  0,137)20×12 
                                        12
       = R762421,9984 = R762 422,00
      Liz has the most money. 
    2. The difference is R762 422,00 – R687 174,49 = R75 247,51.
      [6] 

6.6.3 Using the Present Value formula

  • You can borrow a large amount of money from the bank. This is called a loan. For example, there are student loans to pay for further studies, vehicle loans to buy a car and loans to buy a house.
  • A bond or mortgage or a home loan is a loan used to buy a house or other property.
  • The amount you must pay back is the total of the loan and the interest charged on it. You must pay back an equal amount each month called a monthly installment.

Each month, the interest is calculated on the amount you still owe. Because you are paying back the same amount monthly, the amount you owe is decreasing.
Here is a formula to work out your monthly installments. It is called the Present Value Formula. It is present because you receive the money now in the present. You start paying it back at the end of the first month of the loan.

P =  x [ 1 −  (1 + i) −n ) ]
                     i
where P is the Present value
x is the monthly installment
i is the interest rate p.a.
n is the number of time periods to repay the loan
This formula is provided on the information sheet in the final exam. 


e.g.13
A loan of R240 000 is repaid over 5 years with equal monthly payments (installments), starting one month after the loan was granted.
Notice: it is normal to start paying back a loan one month after it was granted.

  1. Calculate the monthly repayments if the interest on the loan is 9% p.a. compounded monthly.
  2. The client has financial difficulties and makes only 17 payments.
    Calculate the balance of the loan at the end of the 17th month.
Solutions
4

The balance of a loan that must be paid at any particular time during the agreed loan time, can be calculated by using the present value formula for the remaining number of installments.

Activity 7

  1. In order to buy a car, Zack takes out a loan of R25 000 from the bank. The bank charges an annual interest rate of 11% compounded monthly. The installments start a month after he has received the money from the bank.
    1. Calculate his monthly installments if he has to pay back the loan over a period of 5 years.
    2. Calculate the outstanding balance of his loan after two years (immediately after the 24thinstalment). (8)
  2. Jill negotiates a loan of R300 000 with a bank which has to be repaid by means of monthly payments of R5 000 and a final payment which is less than R5 000.The repayments start one month after the granting of the loan. Interest is fixed at 18% per annum, compounded monthly
    1. Determine the number of payments required to settle the loan.
    2. Calculate the balance outstanding after Jill has paid the last R5 000.
    3. Calculate the value of the final payment made by Jill to settle the loan.
    4. Calculate the total amount Jill repaid to the bank. (13)
      [21]

Solutions

    1. P = R25 000; i = 11% monthly = 0,11 x i s the monthly installment
                                                                   12
      n = 5 × 12 = 60
      5
      His monthly installment will be R543,56 (to the nearest cent)
    2. 5 years × 12 months = 60 months. He still has to pay for 60 – 24 = 36 months.
      6
      The outstanding balance after two years will be R16 602,97
      (to the nearest cent).(8)
    1. P = 300 000 x = 5 000 i = 0,18 = 0,015 3 n = ?
                                                 12
      P = x [ 1 – (1 + i) –n ]
                        i
      300 000 = 5000 [ 1 – (1 + 0,015) –n ]
                                   0.015
      300 000 × 0,015 = 5 000 [1 – (1,015)–n]
      4500 – 1 = – (1,015)–n
      5000
      – (1,015)–n = –0,1
      – n =  log 0,1 
              log 1.015
      n =154,65
      ∴ Number of payments = 155
    2. 7
    3. Amount paid in last month
      = 3230,50 ( 1 + 0,18)
                                 12
      = R3278, 96
    4. Total repaid = (154 × 5000) + 3278,96 = R773278,96 3 (13)
      [21] 

Since n = 154,6541086, the outstanding period to cover the whole loan is 0,6541086
There are 154 equal monthly payments of R5 000 plus the last instalment which is less than R5 000

Activity 8

  1. A farmer buys a tractor for R450 000.
    1. How much will the tractor be worth in 5 years’ time if its value depreciates at 9% per annum on a reducing balance? (3)
    2. After 5 years, the tractor needs to be replaced. During this time, inflation remains constant at 7% per annum. Determine the cost of a new tractor after 5 years. (3)
    3. He plans to sell this tractor at its book value and use the money towards a new tractor. Calculate how much money he will need to put into a Sinking Fund to buy a new tractor in 5 years’ time. (1)
    4. Calculate the value of the monthly payment into the sinking fund if the interest is 8,5% p.a. compounded monthly over the next 5 years. (4)
  2. Timothy buys furniture to the value of R10 000. He borrows the money on 1 February 2010 from a financial institution that charges interest at a rate of 9,5% p.a. compounded monthly. Timothy agrees to pay monthly installments of R450. The agreement of the loan allows Timothy to start paying these equal monthly installments from 1 August 2010.
    1. Calculate the total amount owing to the financial institution on 1 July 2010. (2)
    2. How many months will it take to pay back the loan? (6)
    3. What is the balance of the loan immediately after Timothy has made the 25th payment? (4)
  3. Calculate how many years it will take for an investment to treble (becomes three times as big) if it is invested at 12% per annum compounded half-yearly. (5)
    [28]

Solutions

    1. Use compound depreciation with P = R450 000, i = 0,09,
      n = 5 years.
      A = P (1 – i)n
      A = 450 000 (1 – 0,09)5 
      A = 280 814,4653
      The tractor will be worth R 280 814,47 in 5 years’ time. 
      (This is what its ‘book value’ or ‘scrap value’ will be in 5 years’ time) (3)
    2. Use compound interest for inflation with P = R450 000, i = 0,07,
      n = 5 years.
      A = P(1 + i)n
      A = 450 000 (1 + 0,07)5 
      A = 631 148.2788
      A new tractor will cost R631 148,29 in 5 years’ time. (3) 
    3. Cost of new tractor – book value of old tractor)
      = R631 148,29 – R280 814,47
      = R350 333,82 in a Sinking Fund.
    4. Use the Future value formula and solve for x.
      F = R350 333,82x is the monthly installment
      i = 8,5% compounded monthly =0.085/12 n = 5 × 12 = 60 months
      8
      The monthly payment into the sinking fund over the next 5 yearsThe monthly payment into the sinking fund over the next 5 yearsneeds to be R4 706,10 (rounded off to the nearest cent)(4)
  2.  
    1. A = 10000 ( 1 +A = 10000 ( 1 + 0.095/12)5
      = R10 402,15 (2)

    2.  9
    3. Balance outstanding after 25 months
      = 25, 6315128204… – 25
      = 0, 6315128204 
      10
  3. Let x be the P, the investment in rand.
    So the final amount A will be three times as much: 3x Rand.
    i = 12% compounded half-yearly (twice a year) = 0,12
                                                                                     2
    A = P (1 + i)n
    3x = x ( 1 + 0,12)n×2 
                         2
    3x = (1,06)2n
     x
    3 = (1,06)2n Use logs to find n
    2n = log1,06 3 
    2n = 18,85
    n = 9,42708834…
    It will take more than 9 years, so we say that the answer is 10 years.
    It will take 10 years for an investment to treble if interest of 12% is compounded half-yearly. (5)
    [28]

Multiply 10 402,15 by (  0.095 ) and then divide by 450.
                                        12
Write in log form to calculate the value of n (the number of months to pay back the loan).

What you need to be able to do:

  • Use the simple and compound growth formulae to solve problems.
  • Use the simple and compound decay formulae to solve problems.
  • Calculate the effect of different compounding periods on the effective interest rate when given the nominal interest rate and calculate the nominal interest rate when given the effective interest rate.
  • Use the Present Value Formula for loans, etc.
  • Use the Future Value Formula for annuities, savings, etc.
  • To calculate the outstanding balance at any given time.
  • To calculate the sinking fund.
Last modified on Wednesday, 08 September 2021 11:56
Published in Grade 12 Mathematics Study Guide and Notes

Related items

More in this category: « TRIG FUNCTIONS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES CALCULUS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES »
back to top