CALCULUS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- Average gradient
- Average rate of change
- The derivative of a function at a point
- Uses of the derivative
- Drawing the graph of a cubic polynomial
7.1 Average gradient
The gradient of a straight line can be calculated using m = y2 − y1
x2 - x1
Activity 1
- Determine the average gradient of the graph of y = 5x2 – 4 between x = –4 and x = –1
- Is the function increasing or decreasing between x = –4 and x = –1? (3)
- Determine the average gradient of the graph of y = 5x2 –4 between:
- x = 1 and x = 3
- x = 2 and x = 3
- x = 2,5 and x = 3
- x = 2,99 and x = 3 (8)
- Calculate the average gradient of the curve f(x) = x(x + 3) between x = 5 and x = 3.
- What can you deduce about the function f between x = 5 and x = 3? (3)
[14]
Solutions
|
Use the equation of the curve y = 5x2 –4 to calculate the y-values.
Use the y2 − y1 formula to calculate the gradient.
x2 - x1
Calculate the gradient of a curve?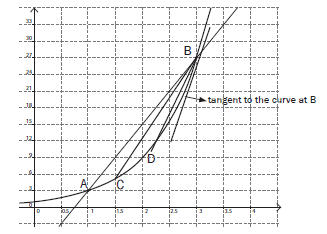
- The average gradient between two points on a curve is equal to the gradient of the straight line through the points. So the average gradient of curve AB is 12.
- As the two points are moved closer together, the average gradient approaches the gradient of the curve which is also the gradient of the tangent to the curve at that point. So the gradient of the curve AB at point B is 30.
- Remember that the tangent is a line that touches a curve at one point only.
- The average gradient tells us whether the graph is increasing or decreasing between those points.
- If the function is decreasing between two points, the average gradient will be negative.
- If the function is increasing between two points, the average gradient will be positive.
7.2 Average rate of change
The average rate of change between two points on a graph is the average gradient of the line joining the two points.
If the graph shows distance as a function of time, the average gradient is change of distance
change in time
This is the average speed = Δdistance
Δtime
e.g.1
- The average rate of change between A and B shown in the graph is 27 − 3 = 24 = 12.
3 - 1 2
- If the distance travelled (in metres) is given by the equation s(t) = t2, where t is the time in seconds, then the average speed between
t = 3 seconds and t = 5 seconds is 52 - 32 = 25 - 9 = 16 = 8 m/s.
5 - 3 2 2
7.3 The derivative of a function at a point
The rate of change of a function at a point is called a derivative.
The derivative of a function at a point gives
- the rate of change of the function at the point
- the slope (gradient) of the tangent to the function at the point
Definition of a derivative
| The derivative of a function y = f(x) is defined as f ´(x) = lim f(x + h) − f(x) h➞0 h This formula is provided on the information sheet in the final exam. |
| NOTE: The notation we use for the derivative of y = f(x) is f ´(x) or y ´ or dy or Dx[f(x)]. dx When we find the derivative of a function, we say we differentiate the function. |
7.3.1 The derivative from first principles
(Definition)
To differentiate from first principles (definition) use the formula below
f ´(x) = lim f(x + h) − f(x)
h➞0 h
f ´(x) is the rate of change of f at x
e.g.2
Determine f ´(x) from first principles if f(x) = –3x2
| Solution Method 1 f(x + h) = − 3(x + h)2 = −3(x2 + 2xh + h2) = − 3x2 − 6xh − 3h2 to get f(x + h) we replace x with x + h and get –3(x + h)2 Expand the brackets and Make sure you multiply the –3 with each term in the brackets Substituting into f ´(x) = lim f(x + h) − f(x) the definition of the derivative gives h➞0 h f ´(x) = lim −3x2 − 6xh − 3h2 − (− 3x2) f (x) = –3x2 so h➞0h f(x) = –3x2 = lim −3x2 −6xh −3h2+ 3x2 h➞0 h Take out a common factor of h so you can cancel it with the h in the denominator. As h goes to 0, –6x – 3h goes to –6x. = lim h(− 6x − 3h) h➞0 h = lim (− 6x − 3h) h➞0 = –6x |
Activity 2
- Determine f ´(x) from first principles if f(x) = 5x2 – 4x + 2 (6)
- Determine f ´(x) from first principles if f(x) = 2/x (6)
[12]
Solutions
(6) |
7.3.2 The rules of differentiation
You could find any derivative from first principles, but there are some quick rules to find the derivative. Unless a question asks you to use the definition or to ‘differentiate from first principles’, it is easier to use the rules.
You need to know and be able to use the following rules for differentiating:
Rules
e.g.3 |
Before you use differentiation you might need to simplify or change the format of the expressions:
- Expand brackets e.g. expand (3x + 2)(x – 5) to 3x2 – 13x – 10 because you have no rule for differentiating a product.
So you need separate terms before you can differentiate.
e.g.4
Determine f ´(x) if f(x) = (3x + 2)(x – 5)Solution
f(x) = 3x2 – 13x – 10
∴f ´(x) = 6x – 13 - Rewrite terms which are square roots, cube roots or other roots as exponentials so that you can use the rule: if f(x) = xn then f ´(x) = nxn–1
e.g.5
√x = x½ so d √x = ½x½
dx
Activity 3
- Evaluate Dx[ (x3 – 3)2]
- Find f ´(x) if f(x)= 3√x
- Find d 3√x5
dx - Differentiate f(x) if f(x) = √x4
- Find f ´(x) if f(x) = √16x3
[11]
 Rewrite terms which are ‘fractions’ where x is part of the denominator, 1/xn as x−n so that you can use the rule: if f(x) = xn then f ´(x) = nxn–1
Rewrite terms which are ‘fractions’ where x is part of the denominator, 1/xn as x−n so that you can use the rule: if f(x) = xn then f ´(x) = nxn–1
e.g.6
Find f ´(x) if f(x) = 3x 2
4x3
| Solution f(x) = 3x2 = 3 x−1 4x3 4 So f ´(x) = − 3 x−2 = − 3 4 4x2 |
Activity 4
- Determine, using the rules of differentiation: dy if y = √x - 1 (3)
dx 2 6x3 - Evaluate dy if y = 4 - x 3
dx √x 9 (3) - Determine Dx [ 6x + 5 ] (4)
3x2
[10]
Solutions
|
7.4 Uses of the derivative
The derivative has many uses.
It can be used to:
- find the gradient of the equation of a tangent line
- identify stationary points on a graph
- find a maximum or minimum value
- describe rates of change
- draw graphs of cubic functions.
- (A cubic function has the form f(x) = ax3 + bx2 + cx + d)
7.4.1 Finding the equation of a tangent line
The slope of the tangent line to the graph at a point is equal to the derivative of the function at that point. So, to find the equation of the tangent line to f(x) at x = a, we must:
- Find the derivative f ´(x)
- Work out the derivative at x = a → i.e calculate f ´(a) to get the gradient of the tangent line.
- Calculate the y value at x = a →i.e calculate f(a).
- The tangent line is a straight line.
We can find the equation of a straight line using y – y1 = m(x – x1) if we know the gradient m and a point (x1; y1) on the line.
e.g.7
Find the equation of the tangent to the function f(x) = x3 + 2x + 4 at the point where x = 1.
| Solution f ´(x) = 3x2 + 2 1. Take the derivative f ´(1) = 3(1)2 + 2 = 5 2. Find the gradient of the tangent at x = 1 by so m = 5 evaluating the derivative at x = 1. f(1) = 1 + 2 + 4 = 7 3. Calculate the y-value at x = 1 Tangent line: y – 7 = 5(x – 1) 4. Use y – y1 = m(x – x1) to give the equation of the tangent line y – 7 = 5x – 5 y = 5x + 2 So the equation of the tangent at x = 1 is y = 5x + 2 |
7.5 Drawing the graph of a cubic polynomial
A cubic polynomial is a function of the form f(x) = ax3 + bx2 + cx + d and we can represent it with a graph. In order to draw the graph, we need to work out the characteristics of the graph.
- We can use the derivative to identify the slope of the graph at certain points.
- We also need to know how to solve equations in the third degree, so that we can work out the x- and y-intercepts of the graph.
7.5.1 Solving equations in the third degree:
ax3 + bx2 + cx + d = 0
e.g.8
Work through this example:
Factorise and solve for x: x3 – x2 – 5x = 3
Solutions
|
7.5.2 Stationary points of a cubic function
Stationary points on a graph are points where the gradient of the graph is 0. This is at points where the direction of the curve of the graph changes.
On a cubic function, the stationary points are at local maximum or minimum turning point. There are also situations where a point of inflection can also be a stationery point as indicated on figure 2 of the example below.
NOTE: A point of inflection is not always a stationary point.
e.g.9
The turning points are only local because the end points of the graphs are often greater than the local maximum or less than the local minimum.
figure 1
The derivative f ´(x) gives us the slope of a graph.
So to find the coordinates of the turning points of a function f(x), we solve f ´(x) = 0.
To find the coordinates of the point of inflection, find the derivative of the derivative, f ´´(x). This is called the second derivative. Solve for f ´´(x) = 0.
7.5.3 Drawing the graph of a cubic function
To draw a graph of a cubic function, follow these steps:
- Find the y-intercept by finding f(0). When x = 0, what is the value of y?
- Find the x-intercepts by finding x value(s) where f(x) = 0. Factorise f(x) to be able
to work out these values.
Identify one factor using the factor theorem.
The factor theorem: If f(k) = 0, then x – k is a factor of f(x). - Find the stationary points or turning point by solving f ´(x) = 0.
NB: The three steps indicated above are very important. Sketch graph should have all the above points with correct identification of the shape explained below. - Identify the end behavior i.e. identify what happens to the graph for very large positive and negative values of x.
- If a > 0, then f(x) is positive for very big values of x and negative for very big negative values of x.
- If a < 0, then f(x) is negative for very big values of x and positive for very big negative values of x.

e.g.10
Sketch the graph of f(x) = x3 – 4x2 – 11x + 30.
- y-intercept: When x = 0, f(0) = 30 so y-intercept is at (0; 30).
(You need to learn the steps of drawing a cubic polynomial!) - x-intercepts: Test some values of x (choose factors of 30)
f(1) = 16 so (x – 1) is not a factor. f(–1) = 36 so (x + 1) is not a factor.
f(2) = 0 so (x – 2) is a factor.
Choose Method I, II or III above to continue. Here is the synthetic method.
This method is very quick once you can use it accurately.
∴ x3 – 4x2 – 11x + 30 = (x – 2)(x2 – 2x – 15)1st
coeff2nd
coeff3rd
coeff4th
coeff2 1 -4 -11 30 1 2 -4 -30 -2 -15 0
∴ x3 – 4x2 – 11x + 30 = (x – 2)(x – 5)(x + 3) Factorise the trinomial
So when y = 0, (x – 2) = 0 or (x – 5) = 0 or (x + 3) = 0
∴ x = 2, x = 5 or x = –3.
x-intercepts are at x = 2, x = 5 or x = –3 i.e (2; 0) ; (5; 0) or (-3; 0)
A positive cubic A negative cubic a > 0 a < 0 - Stationary points or turning points:
f ´(x) = 3x2 – 8x – 11
When f ´(x) = 0, then 3x2 – 8x – 11 = 0
(x + 1)(3x – 11) = 0
x = –1 or x = 11/3
y-values at stationary points: f(–1) = –1 – 4 + 11 + 30 = 36 and
f (11/3) = (11/3)3 = 4(11/3) - 11(11/3) + 30 = -14.81 ∴ (− 1;36) and (11/3 , -14.81) - Point of inflection:
f ´(x) = 3x2 – 8x – 11
f ´´(x) = 6x – 8.
6x – 8 = 0 where x = 8/6 = 4/3 , so point of inflection is at x = 4/3
y-value at point of inflection:
f (4/3 )= 10,59. ∴ ( 4/3 ; 10,59) - End behaviour: a > 0 is positive for very big values of x and negative for very big negative values of x.
- Plot the points and the end behaviour.
Join the points in a smooth curve.
Activity 5
- f(x) = − x3 − x2 + x + 10
- Write down the coordinates of the y-intercept of f
- Show that (2; 0) is the only x-intercept.
- Calculate the coordinates of the turning points of f
- Sketch the graph of f. Show all intercepts with axes and all turning points.
- Determine the point of inflection. (17)
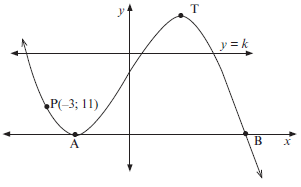
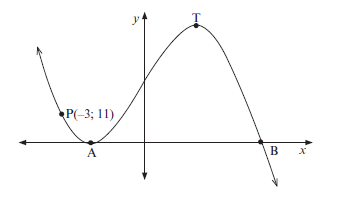
- Sketched below is the graph of g(x) = –2x3 – 3x2 + 12x + 20 = –(2x – 5)(x + 2)2. A and T are turning points of g. A and B are the x-intercepts of g. P(–3; 11) is a point on the graph.

- Determine the x-coordinate of T.
- Determine the equation of the tangent to g at P(–3; 11) in the form y = …
- Determine the value(s) of k for which –2x3 – 3x2 + 12x + 20 = k has three distinct roots.
- Determine the x-coordinate of the point of inflection. (14)
[31]
Solutions
|
7.5.4 Finding the maximum or minimum
f ´(x) = 0 shows us the local maximum or minimum points. We can use this to solve an applied problem that asks for a maximum or minimum value.
This is revision of Grade 10 work that is needed in order to help you with some Grade 12 questions about measurement, volume, maximums and minimums. You need to know these formulae and use them to solve problems.
| 2-D shapes | 3-D shapes Right prisms | 3-D shapes Where the base is a polygon and the sides meet at one point, the apex. |
| Area & Perimeter (The distance around the outside) | V =Area of base × ⊥ height & Surface area = the sum of the areas of the flat shapes | V = 1/3 Area of base × ⊥ Height = 1/3 A × H Where H is the perpendicular height & Surface area = Area of base + ½ ph where p is the perimeter of the base and h the slant height |
1. Circle A = πr2 Circumference = 2πr Circumference = 2πr | 1. Right cylinders V = πr2 × h Surface area = 2πr2 + 2πrh | 1.Cones radius circular base slant height perpendicular height V = 1/3 πr2 × H Surface area = πr2 + ½ (2πr × h) = πr2 + πrh |
2. Square A = length × length = a2 Perimeter = 4a | 2. Square prism  Note: l = b = h = a V = a × a × a = a3 Surface area = 6a2 | 2. Square base pyramid V = 1/3 a2 × H Surface area = area of square + 4 × area of triangle = a2 + 4 ( ½ ⋅ a ⋅ h ) = a2 + 2ah |
3. Rectangle Area: A = length × breadth = ab Perimeter = 2a + 2b | 3. Rectangular prism V = l × b × h Surface area = 2lb+2lh+2bh | The slant height runs from the middle of the edge of the base to the apex. We calculate the slant heights using the perpendicular height and the dimensions of the base by using the Theorem of Pythagoras. |
4a. Right-angled triangle Area: A = ½ × base × height = ½× b × a Perimeter = a + b + c 4b. Triangle  Area: V = ½ × base × ⊥ height = ½ × b × h Perimeter = a + b + c | 4. Triangular prism V = ( ½ × b × h ) × H Surface area of triangular prism = 2 × area of triangle + (sum of areas of 3 rectangles) | 4. Triangular base pyramid V = 1/3 area of base triangular × H Surface area = area of base triangular + (sum of areas of 3 triangles) |
| 2-D shapes 1. Circle  A = πr2 Circumference = 2πr | 3-D shapes 1. Spheres  V = 4/3 πr3 Surface area = 4πr2 | CONVERSIONS 1 millilitre = 1cm3 1 m3 = 1000 litres |
Activity 6
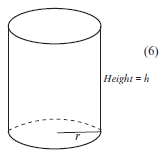
- A drinking glass, in the shape of a cylinder (shown here), must hold 200 ml of liquid when full.
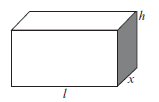
Find the value of r for which the total surface area of the glass is a minimum. - A rectangular box is constructed in such a way that the length (l) of the base is three times as long as its width. The material used to construct the top and the bottom of the box costs R100 per square metre. The material used to construct the sides of the box costs R50 per square metre. The box must have a volume of 9 m3. Let the width of the box be x metres.

2.1 Determine an expression for the height (h) of the box in terms of x.
2.2 Show that the cost to construct the box can be expressed as
C = 1200 + 600x2
x
2.3 Calculate the width of the box (that is the value of x) if the cost is to be a minimum. - A tourist travels in a car over a mountainous pass during his trip.
The height above sea level of the car, after t minutes, is given as s(t) = 5t3 − 65t2 + 200t + 100 metres. The journey lasts 8 minutes.
3.1 How high is the car above sea level when it starts its journey on the mountainous pass?
3.2 Calculate the car’s rate of change of height above sea level with respect to time, 4 minutes after starting the journey on the mountainous pass.
3.3 Interpret your answer to QUESTION 3.2.
3.4 How many minutes after the journey has started will the rate of change of height with respect to time be a minimum? (3)
[26]
Solutions
|
What you need to be able to do:
- Determine the average gradient between two points on a curve
- Differentiate from first principles
- Differentiate using the rules
- Determine the equation of tangents
- Use the Remainder and Factor theorem to find factors of equations in the third degree
- Solve equations in the third degree
- Draw a sketch graph of a cubic function using the x- and y-intercepts, turning points and/or stationary points
- Determine the coordinates of the point of inflection
- Discuss the nature of stationery points including local minimum, local maximum and points of inflection
- Use differentiation to maximise or minimise an equation


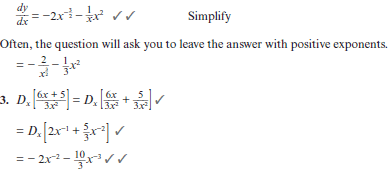

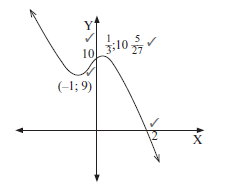 (4)
(4)