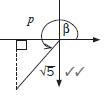TRIGONOMETRY GRADE 12 NOTES - MATHEMATICS STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- Revise: Trig ratios
- Trig ratios in all the quadrants of the Cartesian plane
- Solving triangles with trig
- Using a calculator to find trig ratios
- The trig ratios of special angles
- Using reduction formulae
- Trigonometric identities
- More trig identities
- Solving trigonometric equations
- More solving trig equations using identities
- Compound and double angle identities
- Determining x for which the identity is undefined
10.1 Revise: Trig ratios
Trigonometry is the study of the relationship between the sides and angles of triangles.
The word trigonometry means ‘measurement of triangles’.
The trigonometric ratios
Using θ as the reference angle in ∆ABO
- The side opposite the 90° is the hypotenuse side, therefore side AO is the hypotenuse side.
- The side opposite θ is the opposite side, therefore AB is the opposite side.
- The side adjacent to θ is called the adjacent side, therefore OB is the adjacent side.

We work with the ratios of the sides of the triangle:
- The ratio opposite is called sine θ (abbreviated to sin θ)
hypotenuse - The ratio adjacent is called cosine θ (abbreviated to cos θ)
hypotenuse - The ratio opposite is called tangent θ (abbreviated to tan θ)
adjacent side
We can also place the same triangle on the Cartesian plane in standard position, with a vertex at the origin and one side on the x-axis like this:
- On the Cartesian plane, A is the point (x; y).
- The angle AOB or θ is positive (we rotate in an anti-clockwise direction)
- The length of OB is x units and the length of AB is y units.
- We can find the length of AO, using the Theorem of Pythagoras.

In ∆ABO, AO2 = AB2 + OB2
AO2 = x2 + y2
r2 = x2 + y2
Now we can name the trigonometric ratios in terms of x, y and r.
- The ratio y/r is called sin θ
- The ratio x/r is called cos θ
- The ratio y/x is called tan θ
Learn these ratios:
sin θ = y/r = opposite
hypotenuse
cos θ = x/r = adjacent
hypotenuse
tan θ = y/x = opposite
adjacent
Remember the word SOHCAHTOA:
SOH
sin θ = O
H
CAH
cos θ = A
H
TOA
tan θ = O
A
The Theorem of Pythagoras In any right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
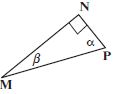
Activity 1
- ∆ MNP is a right-angled triangle. Write down the trig ratios for:
- sin α
- sin β (4)
- tan β
- cos α (3)
- If MP = 13 and NP = 5, calculate cos β.

[7]
Solutions
|
Angles measured in an anticlockwise direction from the x-axis are positive
Angles measured in an anticlockwise direction from the x-axis are negative.
∴angle is negative
10.2 Trig ratios in all the quadrants of the Cartesian plane
The Cartesian plane has four quadrants (quarters). We label them 1, 2, 3 and 4 starting from the quadrant with positive x- and y-values. We can calculate trig ratios for any angle size in the Cartesian plane.

- In the first quadrant x, y and r are positive. Therefore, all the trig functions are positive.
- In the second quadrant, y and r are positive, therefore sin θ is positive. In the second quadrant, x is negative, therefore cos θ and tan θ are negative.
- In the third quadrant, x and y are negative, therefore tan θ is positive.
In the third quadrant, r is positive, therefore cos θ and sin θ are negative - In the fourth quadrant, x and r are positive, therefore cos θ is positive. In the fourth quadrant, y is negative, therefore sin θ and tan θ are negative.
Activity 2
- If sin θ is negative and cos θ is positive, then which statement is true?
- 0° < θ < 90°
- 90° < θ < 180°
- 180° < θ < 270°
- 270° < θ < 360° (1)
- If tan θ < 0 and cos θ < 0, then which statement is true?
- 0° < θ < 90°
- 90° < θ < 180°
- 180° < θ < 270°
- 270° < θ < 360° (1)
- Will the following trig ratios be positive or negative?
- sin 315°
- cos (–215°)
- tan 215°
- cos 390° (4)
[6]
Solutions
|
10.3 Solving triangles with trig
For some trigonometry problems, it is helpful to draw a diagram showing the angle involved and the x, y and r values.
e.g.1
If tan θ = – √3 and 180° < θ < 360°, determine, using a diagram, the value of:
- sin θ
- 3 cos θ
Solutions
|
Activity 3
If cos β = p/√5 where p < 0 and β ∈ [180°; 360°], determine, using a diagram, an expression in terms of p for:
- tan β
- 2 cos2β – 1
[6]
Solutions
|
10.4 Using a calculator to find trig ratios
The scientific calculator calculates trigonometric ratios as decimal fractions.
e.g.2
- sin 58° = 0,8480480962…. [Press: sin 58 =]
- cos 222° = –0,7431448255… [Press: cos 222 =]
- Calculate (correct to 2 decimal places):
cos 238° tan 132° = 0,5885349 … ≈ 0,59 (to 2 decimal places)
[Press: cos 238 × tan 132 =] - sin2 327 = 0,05155 … ≈ 0,052 [NOTE: sin2 327° = (sin 327°)2]
5+tan 37 - sin 30° = ½
10.5 The trig ratios of special angles
- Special trig ratios using the unit circle
Consider a circle on the Cartesian plane that has a radius of one unit.
We can find the trig ratios for 0° (or 360°), 90°, 180° and 270° using the unit circle.
Label the (x; y) coordinates on each axis.
Label the angles on each axis.
From the unit circle:- At 0 or 360°: x = 1, y = 0 and r = 1
- At 90°: x = 0, y = 1 and r = 1
- At 180°: x = –1, y = 0 and r = 1
- At 27°: x = 0, y = –1 and r = 1
sin 0° = 0/1 = 0 sin 90° = 1/1 = 1
cos 0° = 1/1 = 1 cos 90° = 0/1 = 0
tan 0° = 0/1 = 0 tan 90° = 0/1 is undefined
sin 180° = 0/1 = 0 sin 270° = -1/1 = –1
cos 180° = -1/1 = –1 cos 270° = 0/1 = 0
tan 180° = -0/1 = 0 tan 270° = -0/1 is undefined
Summaryθ 0° 90° 180° 270° 360° sin θ 0 1 0 -1 0 cos θ 1 0 -1 0 1 tan θ 0 undefined 0 undefined 0
- Special trig ratios using an equilateral triangle
We use an equilateral triangle that has sides of 2 units to find the trig ratios for the special angles 30° and 60°. The perpendicular bisector of one side creates two triangles. The angles of an equilateral triangle are equal, so angles P, Q and R are each 60°.
P is bisected, so QPS =RPS = 30°.
By Pythagoras,
PR2 = PS2 + RS2
22 = PS2 + 12
PS2 = 4 – 1 = 3
∴ PS = √3
Now we can use ∆PQS to work out trig ratios of 30° and 60°.
sin 60° = √3/2 sin 30° = ½
cos 30° = √3/2 cos 60° = ½
tan 30° = 1/√3 tan 60° = √3/1 = √3 Special trig ratios using a right-angled isosceles triangle
Use a right-angled isosceles triangle with sides of one unit to work out the trig ratios for 45°. The angles opposite the equal sides are equal, so they are each 45° (sum of angles in ∆).
By Pythagoras,
AC2 = AB2 + BC2
AC2 = 12 + 12
AC2 = 1 + 1 = 2
∴ AC = √2
The hypotenuse will be √2 units.
sin 45° = 1/√2 = √2/2
cos 45° = 1/√2 = √2/2
tan 45° = 1/1 = 1
| Summary of special angles You should memorise the special angles, as you will use them often. You will be asked exam questions where you are not allowed to use a calculator, and must show that you have used the special angles.   If you just remember these three diagrams, you can work out all of the special angles. If you find it difficult to remember the diagrams, then learn this summary of the special angles.
|
10.6 Using reduction formulae
Look at the angles here. If θ < 90°, it is in the first quadrant, therefore θ is an acute angle.
When you divide, you sometimes need to round off to the closest numbers that are easier to divide.
Therefore
- angle (180° – θ) in quadrant II
- angle (180° + θ) in the quadrant III
- angle (360° – θ) in quadrant IV.
You can work out which trig ratios will be positive and which will be negative, according to the quadrants they are in. 
- Reduction formulae
Quadrant II: 180° – θ Quadrant III: 180°+ θ Quadrant IV: 360° – θ sin(180° – θ) = sin θ sin(180° + θ)= –sin θ sin(360° – θ) = –sin θ cos(180° – θ) = –cos θ cos(180° + θ) = –cos θ cos(360° – θ) = cos θ tan(180° – θ) = –tan θ tan(180° + θ) = tan θ tan(360° – θ) = –tan θ 
- Angles greater than 360°
We can add or subtract 360° (or multiples of 360°) and will always end up with an angle in the first revolution. For example, 390° can be written as (30° + 360°), so 390° has the same terminal arm as 30°. - Negative angles:
- (–θ) lies in quadrant IV and is the same as 360° – θ.
sin(–θ) = –sin θ cos(–θ) = cos θ tan(–θ) = –tan θ - (θ–180)lies in the third quadrant
sin(θ –180) = -sin θ cos(θ–180) = –cos θ tan(θ–180) = tan θ - (–θ–180)lies in the second quadrant
sin(–θ –180) = sin θ cos(–θ–180) = –cos θ tan(–θ–180) = –tan θ - (θ–360) lies in the first quadrant
sin(θ– 360) = sin θ cos(θ–360) = –cos θ tan(θ–360) = –tan θ
- (–θ) lies in quadrant IV and is the same as 360° – θ.
e.g.3
sin (360˚+ θ) = sin θ
cos (360˚+ θ) = cos θ
tan (360˚+ θ) = tan θ
Activity 4
Without using a calculator, determine the value of:
- cos 150°
- sin (–45°)
- tan 480°
[7]
Solutions
|
d) Co-functions
In this right-angled triangle, the sides are a, b and c and B = θ.
A = 90° and angles of a triangle are supplementary
∴ C = (90° – θ).
Look at the sine and cosine ratios for the triangle:
sin θ =b/a and cos (90° – θ) = b/a
∴ cos (90° – θ) = sin θ
cos θ = c/a and sin (90° – θ) = c/a
∴ sin (90° – θ) = cos θ
Trig ratios of angles that add up to 90°, are called co-functions.
| sin (90˚– θ) = cos θ (quadrant I) sin (90˚+ θ) = cos θ (sin θ positive in quadrant II) sin (θ – 90˚) = sin[–(90° – θ)] (common factor of –1) = –sin(90° – θ) (sin θ negative in quadrant IV) = –cos θ cos (90˚– θ) = sin θ (quadrant I) cos (90˚+ θ) = –sin θ (cos θ negative in quadrant II) cos (θ – 90˚) = cos[–(90° – θ)] (common factor of –1) = +cos(90° – θ) (cos θ positive in quadrant IV) = +sin θ |
Activity 5
Write the trig ratios as the trig ratios of their co-functions:
- sin 50°
- cos 70°
- sin 100°
- cos 140°
[4]
Solutions
|
Summary
Any angle (obtuse or reflex) can be reduced to an acute angle by using:
- Convert negative angles to positive angles
- Reduce angles greater than 360°
- Use reduction formulae
- Use co-functions
Activity 6
Simplify without using a calculator:
- sin(180° + x). cos 330°.tan 150° (4)
sin x - cos 750°.tan 315°.cos(–θ) (8)
cos(360°- θ).sin300°.sin(180°- θ) - tan 480°.sin 300°.cos 14°.sin(–135°) (9)
sin104°.cos225° - cos 260°.cos 170° (7)
sin10°.sin190°.cos350°
[28]

10.7 Trigonometric identities
- tan θ = sinθ ; (cos θ ≠ θ)
cos θ
(the quotient identity) - sin2θ =1 – cos2θ
sin2θ + cos2θ = 1
cos2θ = 1 – sin2θ
(the square idedtity)
PROOF OF IDENTITIES Proof: sin2θ + cos2θ |
Activity 7
Simplify the following expressions.
- cos (180°–x) sin (x –90°) – 1 (8)
tan2(540° + x) sin(90°+x)cos(–x) - [sin(–θ) + cos(360° + θ)][cos(θ – 90°) + cos(180°+θ)] (3)
- cos2θ (1 + tan2θ) (3)
- 1 – cos2θ
1– sin2θ (3)
[17]
Solutions
|
10.8 More trig identities
You need to be able to use all the information you have about trig ratios and ways to simplify them in order to solve more complicated trig identities.
Activity 8
Prove the following identities:
sin x ∙tan x + cos x = 1
cos x (4)
(sin x + tan x) ( sin x ) = sin x. tan x (7)
1 + cos x
1 = cos x + tan x (6)
cos x 1 + sin x
1 + tan x = tanx (5)
tanx sin2x
[22]
  |
Hints for solving trig identities:
- Choose either the lefthand side or the righthand side and simplify it to look like the other side.
- If both sides look difficult, you can try to simplify on both sides until you reach a point where both sides are the same.
- It is usually helpful to write tan θ as sinθ
cosθ . - Sometimes you need to simplify sinθ to tan θ.
cos θ - If you have sin2x or cos2x with +1 or –1, use the squares identities (sin2θ + cos2θ = 1).
- Find a common denominator when fractions are added or subtracted.
- Factorise if necessary – specify with examples i.e. common factor, DOPS, Trinomial, sum/diff of two cubes
10.9 Solving trigonometric equations
To solve a trig equation where the angle is unknown, you need to find all the possible values of the angle.
For example, if sin θ =½ , we know that θ could be 30°. However, there are other values for θ in
the other quadrants. Have a look at the graph for sin θ = ½ , θ ∈ [–360°; 720°].
There are six values for θ between –360° and 720°.
If 30° is our reference angle in quadrant I.
In quadrant II: sin (180° – 30°) = sin 30° = _12_ So θ is 150°
In quadrant III and IV, the sine ratio is negative, so there is no solution for θ.
The angle could be greater than 360°.
In quadrant I: sin (360° + 30°) = sin 30° = _12_ So θ is 390°
In quadrant II: sin (540° – 30°) = sin ((540° – 360°) – 30°)
= sin (180° – 30°) = sin 30 = ½ So θ is 510°
You can also work out that θ = –210° or θ = –330°
You do not need to draw a graph to solve these equations.
A method to find the general solution of trig equations:
|
e.g.4
- Solve for x: sin x = 0,7 [On your calculator, press: sin–1 0,7 =]
The calculator answer is 44,42……°
We call this the reference angle, as it is not the only solution to the equation.
sin x is positive, so angle x must be in quadrant I or quadrant II in the first revolution.
In quadrant I: x = 44,42……. °
AND
In quadrant II: x = 180° – 44,42….° = 135,57…….. °
The period of the sin graph is 360°, so the other points of intersection occur 360° to the right or left of these solutions.
We add k revolutions to the two angles in the first revolution.
k is an integer (…–1; 0; 1; …). We call this the general solution of the equation.
So we can say the solution to sin x = 0,7 is x = 44,42° + k360° or x = 135,57° + k360°; k ∈ Z.
(Correct to two decimal place) - Solve for x: sin x = –0,7
This time, place the reference angle in quadrants III and IV (sin x is negative)
x = 180°+ 44,42…..°+ k360° or x = 360°– 44,42…..°+ k360° k ∈ Z
x = 224,42° + k360° or x = 315,57° + k360; k ∈핑
(Correct to two decimal place) - Solve for x: cos x = –0,7 Reference angle = 134,427….°
cos x is negative in quadrants II and III.
x = 360° – 134,43° = 225,57°
x = 134,43° + k360° or x = 225,57° + k360°; k ∈ Z
(Correct to two decimal place) - Solve for x: cos x = 0,7 Reference angle = 45,57……°
This time, place the reference angle in quadrants I and IV where cos x is positive:
x = 45,57….° + k360° or x = 360° – 45,57……° + k360°
x = 45,57° + k360° or x = 314,43° + k360°; k ∈ Z.
(Correct to two decimal place) - Solve for x: tan x = 0,7 tan x is positive in quadrants I and III.
Reference angle = 34,99° (correct to 2 dec places)
x = 34,99….° or 180° + 34,99……° = 214,99…….°
Now the period of the tan graph is 180°, so the other points of intersection occur 180° to the right or left of the solutions.
x = 34,99° + k180°; k ∈핑
(Correct to two decimal place) - Solve for x: tan x = –0,7
tan x is negative in quadrants II and IV.
The reference angle is –34,99…...°
180° – 34,99…….° = 145,01…..°
x = 145,01° + k180°; k ∈ Z.
You do not need to write down the solution of 215°.
This solution is already there because 34,99° + (1)180° = 215°
Activity 9
- If cos 20° = p, determine the following ratios in terms of p:
- cos 380°
- sin 110°
- sin 200° (6)
- Determine the general solution for x in the following equations:
- 5 sin x = cos 320° (correct to 2 decimal places)
- 3 tan x + √3 = 0 (without using a calculator)
- tan x–1 = –3 (correct to one decimal place) (10)
2
- Determine x for x ∈[–180°; 180°] if 2 + cos (2x – 10°) = 2,537 (6)
[22]
Solutions
|
10.10 More solving trig equations using identities
• a sin θ = b cos θ: single sin and cos function with the same angle
Divide by the cos function
Change sin θ to tan θ
cos θ
e.g.5
Solve for x (give general solution) and round off your answer to 2 decimal places.
- 3 sin x = 4 cos x
- 4 cos2 x + 4 sinx cos x + 1 = 0
[6]
Solutions
|
a sin θ = b cos β: single sin and cos function with the different angles
- Use co-functions to get the same function i.e. change the sin function to a cos function or the cos function to a sin function.
- If sinθ = sinβ, we equate the angles then θ = β and θ = 180° – β.
If cosθ = cosβ we equate the angles then θ = β and θ = 360° – β
e,g,6
Solve for x (give general solution) and round off your answer to 2 decimal places.
sin (x + 20°) = cos 3x [7]
| Solution sin (x + 20°) = cos 3x Use co-functions sin (x + 20°) = sin (90° – 3x) Choose one angle to be the reference angle Ref angle = (90° – 3x) x + 20° = 90° – 3x + k360° or x + 20° = 180° – ( 90° – 3x) + k360 4x = 70° + k360° x + 20° = 180° – 90° + 3x + k360° x = 17,5° + k90° –2x = 70° + k360° x = –35° – k180° k ∈ Z [7] |
e.g. 7
- sin2 A − sinA cosA = 0
- cos2A − 2 cosA − 3 = 0
- cos2x + 3 sinx = − 3 [16]
Solutions
|
Trigonometric equations that leads to quadratic equations
10.11 Compound and double angle identities
sin (20° + 30°) ≠ sin 20° + sin 30°
When two angles are added or subtracted to form a new angle, then a compound or a double angle is formed.
Sketch 1 : The compound angle ABC is equal to the sum of α and β
eg. 75° = 45° + 30°
Sketch 2 : The compound angle EGH is equal to the difference between α and β
eg. 15° = 60° – 45° or 15° = 45° – 30°
Sketch 3 : The double angle PTR is equal to the sum of α and α
eg. 45° = 22,5° + 22,5°
Using the same methods as we did to establish the reduction formulae, we can also establish the compound angle identities.
Given any angles a and β, we can find the values of the sine and cosine ratios of the angles a + β, a – β and 2a.
| sin (α + β) = sin α cos β + cos α sin β sin (α – β) = sin α cos β – cos α sin β cos (α + β) = cos α cos β – sin α sin β cos (α – β) = cos α cos β + sin α sin β sin 2α = 2sin α cos α cos 2α = cos2 α – sin2 α = 2cos2 α – 1 = 1 – 2 sin2 α |
These formulae are provided on the information sheet in the final exam.
You should learn these formulae, as you will use them often.
NOTE:
sin (α + β) ≠ sinα + sinβ and
cos (α – β) ≠ cosα – cosβ
Accept:
cos(α – β) = cosα.cosβ + sinα.sinβ, and derive the other compound angle identities
| These are examinable, learn them well. Proof: cos(α + β) = cos[α – (–β)] = cosα.cos(–β) + sinα.sin(–β) = cosα.cosβ + sinα.(–sinβ) = cosα.cosβ – sinα.sinβ Proof: sin(α + β) = cos[90° – (α + β)] = cos[90° – α – β] = cos[(90° – α) – β] = cos(90° – α). cos(β) + sin(90° – α). sin(β) = sinα.cosβ + cosα.sinβ Proof: sin(α – β) = cos[90° – (α – β)] = cos[90° – α + β] = cos[(90° + β) – α] = cos(90° + β). cosα + sin(90° + β). sinα = –sinβ.cosα + cosβ.sinα = sinα.cosβ – cosα.sinβ |
e.g.8
Simplify without the use of a calculator:
- cos70° cos10° + cos20° cos80°
- 2 sin15° cos 15°
- sin 15° [10]
Solutions
|
Activity 10
Do NOT use a calculator to answer this question. Show ALL calculations. Prove that:
- cos 75° =√2 ( √3 –1) (5)
4 - Prove that cos(90° – 2x).tan(180° + x) + sin2(360° – x) = 3sin2x (7)
- Prove that (tan x – 1)(sin 2x – 2cos2x) = 2(1 – 2sin x cos x) (7)
[19]
|
Activity 11
Determine the general solution for x in the following:
- sin 2x. cos 10° – cos 2x. sin 10° = cos 3x (8)
- cos2 x = 3 sin 2x (11)
- 2sinx = sin(x + 30°) (5)
[24]
Solutions
|
10.12 Determining x for which the identity is undefined
e.g.9
For which values of x is this identity undefined? 1 + tan x = tan x
tan x sin2 x
[4]
Solution 1 + tan x = tan x is undefined if tan x = 0 or if sin²x = 0 or if tan x is undefined |
- any number is undefined.
0
Therefore if the denominator of an identity = 0, then the identity is undefined - y = tanx is undefined for certain value of x.
Therefore if a tan function is in an identity then the identity is undefined where the tan function is undefined.
What you should be able to do:
- Simplify expression, without a calculator by using a sketch.
- Use reduction formulae and/or co-functions
- Use special angles
- Derive and use the trig identities: (Quotient, square, compound and double angle identities).
- Determine for which values an identity is undefined
- Determine the general solution of trigonometric equations
- Solve trigonometric equations with a given interval
- Use identities to prove identities and solve equations