TRIGONOMETRY:SINE, COSINE AND AREA RULES GRADE 12 NOTES - MATHEMATICS STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupWe use these three rules to find the lengths of sides, sizes of angles and the area of any kind of triangle. To ‘solve a triangle’ means you must calculate the unknown sides and angles.
11.1 Right-angled triangles
You can use the trig ratios to find angles and lengths of a right-angled triangle.
Activity 1
In triangle ABC, ^B = 37° and AC = 16 cm. ^C = 90°. Calculate the length of AB and BC (correct to one decimal place). (3)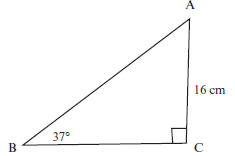
| Solution To calculate the length of AB, use 37° as the reference angle, then AC = 16 cm is the opposite side and AB is the hypotenuse. Use the sine ratio. sin 37° = opp =16 hyp AB AB sin 37° = 16 AB = 16 = 26,6 cm sin37° To find the length of BC, you can use cos 37° = adj = BC/26.6 hyp 26,6 cos 37° = BC BC = 21,2 cm (to one decimal place) You can also use Pythagoras’ theorem: AB2 = AC2 + BC2 [3] [3] |
Activity 2
In triangle PQR, PQ = 12,3 m and PR = 13 m. Calculate the size of ^Q . (2)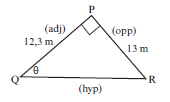
[2]
| Solution Use PQ and PR. tan θ = opp = 13 12.3 θ = tan–1 (13/12.3) = 46,58° [2] |
11.2 Area rule
Area of a right-angled triangle:
Area D = ½ base × perpendicular height
Area D = ½ bh
Proof of Area rule [STUDY FOR EXAM PURPOSE]
If ^A is acute Area of ∆ABC = ½ bh……………(1) But sin A = h/c ∴ h = c sin A Substituting into (1) Area of ∆ABC = ½ bc sin A Similarly it can be shown that Area of ∆ABC = ½ ab sin C = ½ ac sin B | If ^A is obtuse Area of ∆ABC = ½ bh……………(1) But sin (180° – A) = _hc_ ∴ h = c sin A Substituting into (1) Area of ∆ABC = _12_ bc sin A Similarly it can be shown that Area of ∆ABC = ½ ab sin C = ½ ac sin B |
| If a base or height is unknown, you can use trig ratios to work them out. If the perpendicular height is not given and cannot be worked out, then we need a different area formula. There is a formula that works to find the area of any triangle, even if we do not know the perpendicular height. The area of any ΔABC is half the product of two sides and sine of the included angle.  So if you choose to use angle A, then Area ΔABC = ½ bc sin A If you choose to use angle B, then Area ΔABC =½ ac sin B If you choose to use angle C, then Area ΔABC = ½ ab sin C Learn one form of the formula – you can work out the others from that. To find the area of any triangle, you need to know the lengths of two sides and the size of the angle between the two sides. |
e.g.1
Calculate the area of ∆MNK with m = 3,5 cm;
n = 4,8 cm and ^K = 112°.
Choose the version of the formula that uses the sides m and n and the angle K because these are known values.
Area ∆ MNK = ½ mn sin K
= ½ (3,5)(4,8) sin 112°
= 8,4 sin 112°
= 7,788 cm2 (correct to 3 decimal places)
11.3 Sine rule
If you have enough information about the sides and angles of any triangle, you can use the sine rule to find the other sides and angles.
Sine rule
The ratio of sine of the angle divided by the side opposite that angle is the same for all three pairs of sides and angles.
So …
In any triangle ABC:
sinA = sinB = sinC
a b c
We can also use the ratios with the sides in the numerator:
a = b = c
sinA sinB sinC
The formula will be provided on the information sheet
Proof of Sine rule [STUDY FOR EXAM PURPOSE]
If ^A is acute | If ^A is obtuse |
| Using Area rule for ΔABC: ½ bc sin A = ½ ab sin C = ½ ac sin B Dividing each by ½ abc results: sinA = sinC = sinB a c b | |
To use the sine rule you need to know at least one side and its matching opposite angle and one more side or angle. The sine rule can be used to solve many problems if the right information about the triangle is given.
The sine rule can be used to solve many problems if the right information about the triangle is given.
Activity 3
Solve ∆XYZ in which z = 7,3 m, ^X = 43° and ^Y = 96°. Give your solutions correct to 3 decimal places. (4)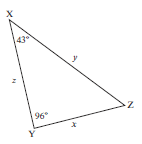
[4]
| Solution The angle opposite the known side is not given, but you can work it out. ^Z = 180° – (43° + 96°) (sum angles of ∆) ^Z = 41° To find y: y = 7,3 sin 96° sin41° y = 7,3 sin 96° sin41° y = 11,066 m Using the sine rule again to find x: x = 7,3 sin43° sin41° x = 7,3 sin 43° sin41° x = 7,589 m [4] |
11.4 Cosine rule
You apply the cosine rule If you are given the values of:
- two sides and the included angle OR
- three sides of a triangle,
Cosine rule:
In any triangle ABC:
If you choose to use angle A, then
a2 = b2 + c2 – 2bc cos A
If you choose to use angle B, then
b2= a2 +c2 – 2ac cos B
If you choose to use angle C, then
c2 = a2 + b2 – 2ab cos C
Proof of Cosine rule [STUDY FOR EXAM PURPOSE]
If ^A is acute A D C In Δ BDC: a2 = BD2 + CD2 (Pythagoras Theorem) = BD2 + (b – AD)2 = BD2 + b2 – 2bAD + AD2 But BD2 + AD2 = c2 (Pythagoras Theorem) Thus a2 = b2 + c2 − 2bAD ……………………..(1) In Δ ABD: cosA =AD ∴ AD = c cos A ………..(2) c Substituting (2) into (1) ∴ a2 = b2 + c2 − 2bc cosA Similarly it can be shown that: b2 =a2 + c2 − 2ac cosB and c2 = a2+ b2 − 2ab cosC | If ^A is obtuse In Δ BDC: a2 = BD2+ CD2 (Pythagoras Theorem) = BD2 + (b + AD)2 = BD2 + b2 +2bAD + AD2 But BD2 + AD2 = c2 (Pythagoras Theorem) Thus a2 = b2 + c2 + 2bAD …………………..(1) InΔABD:. cos(180°- A) = AD ∴ AD = − c cosA……….(2) c Substituting (2) into (1) ∴ a2 = b2 + c2 − 2bc cosA Similarly it can be shown that: b2 = a2 + c2 − 2ac cos B and c2 = a2 + b 2 − 2ab cos C |
e.g.2
- Solve ∆PQR if q = 462 mm, p = 378 mm and ^R = 87°.

Using the cosine rule
(two sides and the included angle are given so you canfind the side opposite the given angle)
PQ2 = p2 + q2 – 2pq cos R
PQ2 = (378)2 + (462)2 – 2(378)(462).cos 87°
PQ2 = 338 048,5159
PQ = 581,42 mm [take square root]
Using the sine rule:
378 = 581,42
sinP sin87°
sin P = sin 87°
378 581,42
(it is easier to have ^P in the numerator)
sin P = 378 × sin 87°
581,42
sin P = 0,649
^P = s in– 1 (0,649) = 40,48°
∴ ^Q = 180° – (87° + 40,48°) = 52,52° [sum angles of ∆] - Determine the biggest angle in ΔABC if a = 7 cm; b = 9 cm and c = 15 cm.
You are given three sides, so use the cosine rule.
The biggest angle will be ^
C (opposite the longest side).
c2 = a2 + b2 – 2 ab cos C
2 ab cos C = a2 + b2 – c2
cos C = a2 + b2 − c2
2ab
rearrange the formula to get cos C on its own
cos C = 72 + 92 − 152
2(7)(9)
cos C = –0,753968… cos θ is negative in quad 2, so ^C is obtuse.
reference angle is 41,06°
^C = 180° – 41,064…° = 138,94° (correct to two decimal places)
11.5 Problems in two and three dimensions
Activity 4
1. PQRS is a trapezium with PQ // SR, PQ = PS, SR = 10 cm,
QR = 7 cm, ^R = 63°.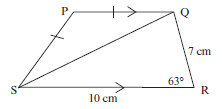
Calculate:
- SQ (2)
- PS (6)
- area of quadrilateral PQRS. (correct to 2 decimal places) (5)
[13]
Solutions
|
When solving triangles, start with the triangle which has most information (i.e. triangle with three sides or two sides and an angle or two angles and a side given)
Activity 5
In the diagram alongside, AC = 7 cm,
DC = 3 cm, AB = AD, DCA = 60°,
DAB = β and ABD = θ.
Show that BD = √37 sin β
sinθ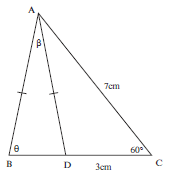
[3]
| Solution AD2 = AC2 + CD2 − 2AC.CD cos 60 ° = (7)2 + (3)2 – 2 × 7 × 3 × 0,5 AD2 =58 – 21 AD2 = 37 AD = √37 P Applying sine rule: BD = AD ⇒ BD = AD sin β but AD = √37 sinβ sinθ sinθ ∴BD = √37 sin β sinθ [3] |
Activity 6
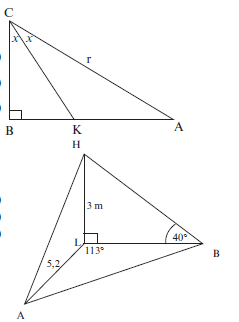
- In the diagram alongside, ABC is a right angled triangle. KC is the bisector of ACB. AC = r units and BCK = x
1.1 Write down AB in terms of x (2)
1.2 Give the size of AKC in terms of x (2)
1.3 If it is given that AK = 2 , calculate the value of x (7)
AB 3
- A, B and L are points in the same horizontal plane, HL is a vertical pole of length 3 metres,
AL = 5,2 m, the angle ALB = 113° and the angle of elevation of H from B is 40°.
2.1 Calculate the length of LB. (3)
2.2 Hence, or otherwise, calculate the length of AB. (3)
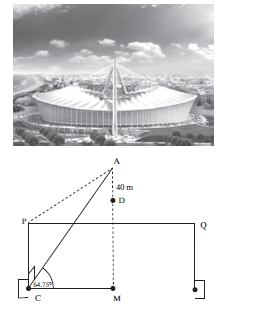
2.3 Determine the area of ∆ABL. (3) - The angle of elevation from a point C on the ground, at the centre of the goalpost, to the highest point A of the arc, directly above the centre of the Moses Mabhida soccer stadium, is 64,75°. The soccer pitch is 100 metres long and 64 metres wide as prescribed by FIFA for world cup stadiums. Also AC ⊥ PC.
In the figure below PQ = 100 metres and PC = 32 metres
3.1 Determine AC (2)
3.2 Calculate PAC (2)
3.3 A camera is placed at D, 40 m directly below point A, calculate the distance from D to C (4)
[28]
| Solutions 1.1 sin 2x = AB ∴ AB = r sin 2x (2) r 1.2 AKC = 90° + x [ext. angle of ∆CBK] (2) 1.3 AK = r ∴ AK = r sinx sin x sin(90° + x) cos x r sin x AK = cos x = r sin x = 1 = 2 AB r sin 2x r cos x.2 cos x sin x 2 cos2x 3 ∴ cos2x = 3/4 cos x = √3/2 Hence x = 30º (7) 2.1 In ∆HLB, tan 40° = 3 LB [∆HLB is right-angled, so use a trig ratio] LB = 3 tan40º LB = 3,5752… ≈ 3,58 metres (3) 2.2 In ∆ABL, [ΔABL not right-angled. You have two sides and included angle, so use the Cosine Rule] AB2 = AL2 + BL2 – 2(AL)(BL).cos L AB2 = (5,2)2 + (3,58)2 – 2(5,2)(3,58).cos 113° AB2 = 54,40410… m2 AB = 7,38 m (3) 2.3 Area ∆ABL = ½ AL × BL × sin ALB = ½ (5,2) × (3,58) × sin 113° = 8,56805… ≈ 8,57 m2 (3) 3.1 cos 64,750° = CM ∴ AC = CM = 50m = 117,21 (2) AC cos64.75° 0.426569 3.2 tanPAC = PC AC PAC = tan−1 (32/AC) = 15,27° (2) 3.3 DC2 = AC2 + AD2 − 2AC.ADcos(90° − 64,75°) DC2 = (117,21 )2 + (40)2 − 2(117,21).40cos(25,25°) = 6857,289 DC = 82,81m (4) [28] |
What you should be able to do:
- Derive and use the trig identities: tan θ = sinθ and sin2θ + cos2θ = 1.
cosθ - Derive and use reduction formulae to simplify θexpressions.
- Determine for which values of a variable an identity is true.
- Derive and use the sine, cosine and area rules.
- Apply the sine, cosine and area rules to solve triangles in 2-D and 3-D problems.
- Use the compound angle and double angle identities where necessary to prove and make necessary calculations.