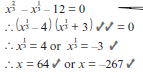EXPONENTS AND SURDS QUESTIONS AND ANSWERS GRADE 12

More in this category: « STATISTICS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES ALGEBRA QUESTIONS AND ANSWERS GRADE 12 »
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

Activity 1
Write in simplest form without using a calculator (show all working).

  1. √8  × √2
  2. 3√4 × 3√2
  3.  9 + √45 
         3
  4. (2  + √5 ) (2  −  √5 )

[10]

Solutions

  1. √8 × √8 = √8×2 = √16 = 4 (1)
  2. 3√4 × 3√2  =  3√4×2 = 3√8  = 2 (2)
  3. 9+ √45 = 9+3√5 = 3( 3+ √5 ) = 3 + √5 (3)
           3             3               3
  4. ( 2 + √5 ) (2  −  √5 )
    = 2 × 2 – √5 × √5 = 4 – 5 = –1 (2)
    Or multiply out the brackets:
    ( 2 + √5 ) (2  −  √5 ) = 4 + 2√5 – 2 √5 – √5 .√5 = 4 – 5 = –1 (2)
    [10] 

Activity 2 Interpret a graph

1. Complete the table for each number by marking the correct columns.        
  Nonreal number  Real number
ℝ 		 Rational number
ℚ 		 Irrational number
ℚ′ 		 Integer
ℤ 		 Whole number
ℕ0 		 Natural number
ℕ 
a) 13               
b) 5,121212…               
c) √–6               
d) 3π               
e) 0 = 0
    9 		              
f) √17               
g)3√64 = 4              
h) 22
     7		              

(23)
2. Which of the following numbers are rational and which are irrational?

  1. √16
  2. √8
  3. √ 9 
       4
  4. √6¼
  5. √47
  6. 22
     7
  7. 0,347347…
  8. π − (− 2)
  9. 2 + √2
  10. 1,121221222… (10)

[33]

Solutions

1. Complete the table for each number by marking the correct columns.        
  Nonreal number  Real number
ℝ 		 Rational number
ℚ 		 Irrational number
ℚ′ 		 Integer
ℤ 		 Whole number
ℕ0 		 Natural number
ℕ 
a) 13     ✓  ✓    ✓  ✓  ✓(5)
b) 5,121212…     ✓  ✓        (2)
c) √–6   ✓            (1)
d) 3π     ✓    ✓      (2)
e) 0 = 0
    9 		    ✓  ✓    ✓  ✓  (4)
f) √17     ✓    ✓      (2)
g)3√64 = 4    ✓  ✓    ✓  ✓  ✓ (5)
h) 22
     7		    ✓  ✓        (2)

2.

  1. √16 (rational)
  2. √8 (irrational) 
  3. √ 9  =  3  (rational)
       4      2
  4. √6¼ =  √25  =  5  (rational)
                  4        2
  5. √47 (irrational) 
  6. 22 (rational)
     7
  7. 0,347347…(rational, because it is a recurring decimal) 3 (1)
  8. π − (− 2) (irrational, because π is irrational) 3 (1)
  9. 2 + √2 (irrational, because √2 is irrational) 3 (1)
  10. 1,121221222…(irrational, because it is a non-recurring and non-terminating decimal) 3 (1)
    [33]

Activity 3
Calculate

  1. −3 (( −2a3)2 + √9a12)     √9a12  = (32a12)½
  2.       5(2a4)3      
    (5a3)2 − 5a6 [5]

Solutions

  1. −3 (( −2a3)2 + √9a12)  simplify exponents inside the brackets and the square root
    = −3(4a6+ 3a6) add like terms inside the bracket  
    = –3(7a6 ) = –21a6 simplify (3)
  2.   5(2a4)3      simplify brackets at the top and the bottom first
     (5a3)2 − 5a6 
     =     5(8a12)     =  40a 12 = 2a6(2)
       +25a6 - 5a6      20a6 
    [5] 

Activity 4
Simplify the following. Write answers with positive exponents where necessary.

  1.   a -3
     b-2
  2.  4a7b-4c-1
       d–2e5
  3.  x–1+ y-1
    [5]

Solutions

  1.  a -3 = b2
     b-2     a3
  2. 4a7b−4c−1 =  4a7d2   
       d-2e5          b4c1e5
  3. x–1+ y–1 = 1  +  1 = y + x
                      x      y      xy
    [5] 

1.3.5 Working with surd (root) signs
The exponential rule 18 can be used to simplify certain expressions.

Activity 5
1. Rewrite these expressions without surd signs and simplify if possible.

  1. 3√5
  2. 4√16
  3. 3√–32
    [3]

10

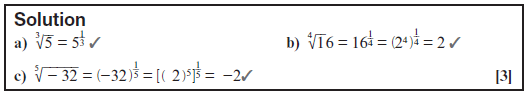
Activity 6
Simplify the following and leave answers with positive exponents where necessary:
(a4)n–1. ( a2b)–3n
    (ab)–2n. b–n
[4]

Solution
(a4)n–1. ( a2b)–3n = a4n−4 . a– 6n . b−3n
    (ab)–2n. b–n           a−2n. b−2n . b–n
=  a4n–4 – 6n +2 n . b −3n + 2n + n
=  a−4 . b0 
= 1  . 1 =  1 
  a4         a4 
[4] 

Activity 7
Simplify the following and leave answers with positive exponents where necessary:

  1.  273 - 2x.9x-1
             812-x

  2.  6.5x +1 - 2.5x +2
              5x+3

  3. 22009 − 22012 
             22010 [13]

Solutions

  1. . 27 3−2x . 9x−1= (33)3−2x . (32)x−1  = 39−6x. 32x−2
               812-x                (34)2−x                  38-4x
    = 3 9−6x+2x−2−8+4x 
    = 3 −1  = 1 
                  3 (4)

  2.  6.5x +1 - 2.5x +2 =  6.5x .51  − 2.5x . 52
              5x+3                       5x. 53
    =  30 − 50 = − 20 = − 4
           125        125     25 (4)

  3. 22009 − 22012 = 22009 (1 − 23) = (22009 1 − 8)
             22010             22010                  22010
    = 22009 (− 7)
          22010
    =  22009−22010  ×− 7
    =  2−1 × − 7 = ½ × − 7 = −7/2 (5)
    [13]

Activity 8
Solve for x:

  1. 3 ( 9x+3 ) = 272x–1
  2. 32x–12 = 1
  3. 2x = 0,125
  4. 10x ( x+1 ) = 100
  5. 5x + 5x+1  = 30
  6. 5 2+x – 5x = 5x. 23 + 1
  7. 5x + 15.5 −x  =  2
  8. 19
    {31]

Solutions
Remember: When adding or subtracting terms, you need to factorise first.

  1. 3(9x+3 ) = 272x–1
    31(32)x + 3 = (33)2x - 1 prime bases
    31+2 x+6  = 36 x–3 same bases
    ∴ 7 + 2x = 6x – 3  equate exponents
    –4x = – 3 – 7
    x = −10 =  5 
          − 4      2
    =(3)
  2. 32 x −12  = 1
    32 x –12 = 30 make same bases by putting 1 = 30
    ∴ 2x – 12 = 0 3 equate exponents
    2x = 12
    x = 6 (3)
  3. 2x  = 0,125 convert to a common fraction
    2x  = 125  =  1  =  1  simplify
           1 000    8      23
    2x = 2−3 same bases
    ∴ x = –3 equate exponents (3)
  4. 10 x(x+1) = 100
    10 x(x+ 1) = 102 same bases
      ∴  x (x + 1) = 2 equate exponents
    x 2 + x – 2 = 0 set quadratic equation = 0
    (x + 2)(x – 1) = 0 factorise the trinomial
    x + 2 = 0 or x – 1 = 0 make each factor = 0
    x = –2 3 x = 1 (4)
  5. 52 + x – 5x  =  5x · 23 + 1
    52 + x − 5x – 5x · 23 = 1 like terms
    52 + x – 24·5x  = 1
    52. 5x – 24· 5 x  = 1 factorise (Common Factor)
    5x (52 – 24 )  =  1 33
    5x (1) =  1
    5x  = 50 ∴ x = 03 (4)
  6. 5x +  5x+1   = 30
    5x + 5x. 51 = 30 factorise
    5x (1 + 51 ) = 30 common factor 5x
    5x ( 6 ) = 30 3 divide 30 by 6
    5x = 5 same bases
      ∴ x = 1 3 equate exponents (4)
  7. 5x + 15.5 -x  =  2
    ∴ 5x + 15  =  2
               5x
    × 5 x ∴  5x. 5x + 5 x.15 =  2.5 x 
    ∴  5x.5x + 15 = 2.5 x
    ∴  5x . 5x − 2.5x  + 15 = 0
    ∴ ( 5x − 5 ) (5x + 3 )  = 0
    ∴  5x  = 5 or 5x  =  − 3 (no solution)
    ∴ x = 1 (5)
  8. 20
    [31] 

Activity 9
Solve for x:
15

Activity 10
Solve these equations and check your solutions.
1. √3x + 4 − 5 = 0 (3)
2. √3x − 5 − x = 5 (5)
[8]

Solutions

  1. √3 x + 4  − 5 = 0
    √3 x + 4  = 5 (isolate the radical )
    ( √3 x + 4) 2  =  52  (square both sides of the equation)
    3x + 4 = 25 
    3x = 21
    x = 7
    Check:
    LHS: √3(7) + 4   − 5
     =  √21 + 4   − 5
     =  √25   − 5
     = 0
     = RHS
     ∴ x = 7 is a solution (3)
  2. √3x − 5  − x = 5
    √3x − 5 = x − 5 (always isolate the radical first)
    ( √3x − 5 ) 2 =  ( x − 5)2 (square both sides)
    3x –5 = x2 –10x + 25  Remember: (x– 5 ) 2  ≠  x 2  + 25
    0 = x2 – 13x + 30  (quadratic equation, set  =  0)
    0  = (x – 10)(x – 3 ) (factorise the trinomial and make each factor  =  0)
    x  =  10 or x =  3
    Check your answer:
    If x = 10
    LHS:
    √3(10) − 5 − 10
     =  √25   − 10
     =  −5 = RHS
    If x = 3
    LHS
    √3(3) − 5 − 3
     =  √4  − 3
     =  −1 ≠  RHS (5)
    ∴ x ≠ 3 and only x = 10 is a solution. 
    [8] 

 

Last modified on Friday, 03 September 2021 07:58
Published in Grade 12 Mathematics Study Guide and Notes

Related items

More in this category: « STATISTICS GRADE 12 NOTES - MATHEMATICS STUDY GUIDES ALGEBRA QUESTIONS AND ANSWERS GRADE 12 »
back to top