Tuesday, 24 August 2021 13:24

TRIG FUNCTIONS QUESTIONS AND ANSWERS GRADE 12

More in this category: « FUNCTIONS QUESTIONS AND ANSWERS GRADE 12 FINANCE GROWTH AND DECAY QUESTIONS AND ANSWERS GRADE 12 »
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

Activity 1
Use the graph y = sin x above to answer these questions:

  1. What are the maximum and minimum values of y = sin x? (2)
  2. Write down the domain and the range of y = sin x. (4)
  3. Write down the x-intercepts of y = sin x. (2)
  4. What is the amplitude of the graph of y = sin x? (1)
  5. What is the period of the graph of y = sin x? (1)
    [10]
Solutions   
y = sinx
1 Maximum Values  1 , at x = –270° and 90° 
  Minimum Values –1, at x = –90° and 270° (2)
2 Domain   x ∈ [− 360°;360°], x ∈ ℝ 
  Range   [–1; 1] y ∈ ℝ (4) 
3 x-intercepts  –360°, –180°, 0°, 180° and 360° (2) 
4 Amplitude 1(1)
5 Period 360° (1)
    [10]

Activity 2

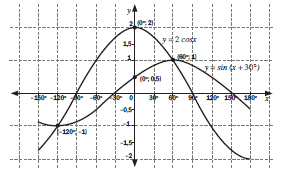
  1. Given f(x) = 2cos x and g(x) = sin (x + 30°)
    1. Sketch the graphs of f and g on the same set of axes for x  ∈ [− 150°; 180°]
      Clearly show all intercepts with the axes and the coordinates of turning points. (7)
      Use your graph to answer the following questions:
    2. Write down the period of f. (1)
    3. For which values of x is f(x) = g(x)? (2)
    4. For which values of x is f(x) > 0? (2)
    5. For which values of x is g(x) increasing? (2)
    6. Determine one value of x for which f(x) − g(x) = 1,5. (1)
    7. If the curve of f is moved down one unit, write down the new equation of f. (2)
    8. If the curve of g is moved 45° to the left, write down the new equation of g. (2)
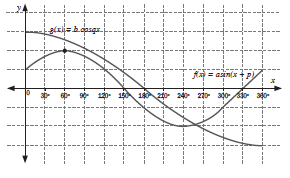
  2. Sketch below are the graphs of g(x) = asin(x+p) and f(x) = bcosqx for x ∈ [0°; 180°]
    10
    1. Determine the numerical values of a, p, b and q. (5)
    2. If the graph of g(x) is shifted two units down:
      1. Write down the amplitude of the new graph (1)
      2. Write down the equation of the new graph (2)
    3. If the graph of f(x) is shifted 60 to the left, write down two possible equations of the new graph. (2)
      [29]

Solutions

  1.  
    1. for g(x) = 2 cos x and for f(x) = sin(x + 30°)
      11
    2. period = 360° (1)
    3. x = –120° or 60°  (2)
    4. for f(x) >0; x ∈ (–90°; 90°)  (2)
    5. g(x) increasing when x ∈ (–120°; 60°) (2)
    6. x = 0° (1)
    7. New f(x) = 2cos x –1 (2)
    8. Original equation: g(x) = sin (x + 30°), with 45° shift to the left:
      g(x) = sin (x + 30° + 45°) so g(x) = sin (x + 75°)  (2)
    1. a = 2 (amplitude of the f(x)) 
      f(x) = 2sin(x+p)… Substitute 60°
      ∴ 2 = 2sin(60° + p)
      ÷ 2 ∴ 1 = sin(60° + p)
      Pressing shift sin −1 (1) = 90°
       ∴ 60° + p = 90° ∴ p = 30°∴ f(x) = 2sin(x + 30°) 
      b=3 (amplitude of the g(x))
      period = 720
      720° =  360°∴ q = ½ ∴ g(x) = 3 cos ½ x (5)
    2. (1) Amplitude = 3 (shift up or down has no effect on the amplitude) (1)
      (2) g(x) = 3 cos ½ x − 2 (2)
    3. f(x) = 2sin(x + 90°) = 2 cos x (2)
      [29] 
Last modified on Monday, 30 August 2021 07:24
Published in Grade 12 Mathematics Study Guide and Notes

Related items

More in this category: « FUNCTIONS QUESTIONS AND ANSWERS GRADE 12 FINANCE GROWTH AND DECAY QUESTIONS AND ANSWERS GRADE 12 »
back to top