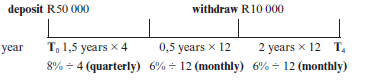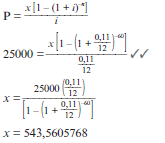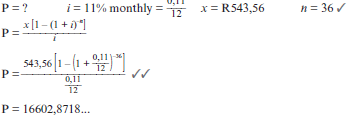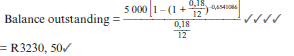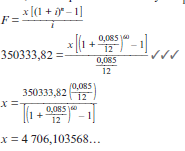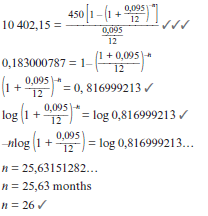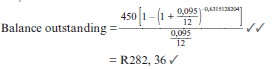FINANCE GROWTH AND DECAY QUESTIONS AND ANSWERS GRADE 12

More in this category: « TRIG FUNCTIONS QUESTIONS AND ANSWERS GRADE 12 CALCULUS QUESTIONS AND ANSWERS GRADE 12 »
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

Activity 1
6.1.1 You invest R1 700 at an interest rate of 10% compounded quarterly. Calculate how much your investment is worth after 6 years. (3)
6.1.2 R25 000 is invested into a savings account. Calculate the value of the investment of the savings after 5 years if interest rates are:

  1. 11% compounded monthly
  2. 11% compounded semi-annually (5)
    [8]

Solutions
6.1.1 A = ? P = R1 700 n = 6 years × 4 = 24
i = 10% compounded quarterly
so divide by 4 i = 0,10
                              4
A = P(1 +i)n
A = 1 700 ( 1  +  0,10/4)24
= R3 074,83 (to nearest cent) (3)
6.1.2

  1. A = R25 000 i = 0,11 n = 5 × 12
                              12
    A = 25 000 ( 1 + 0,11)5 × 12
                                12
    = R43 222,89 
  2. A = R25 000 i = 0,11 n = 5 × 2
                                2
    A = 25 000 ( 1 + 0,11)5 × 2
                                2
    = R42 703,61 (5)
    [8] 

Activity 2

  1. Mary borrowed a certain sum of money from a bank at a compound interest rate of 15% calculated quarterly. After 3 years she now owes R7 000. How much did she borrow? (3)
  2. R1 570 is invested at 12% p.a. compound interest. After how many years will the investment be worth R23 000? (4)
  3. R2 000 was invested in a fund paying interest compounded monthly.
    After 18 months the value of the fund was R2 860, 00. Calculate the interest rate. (4)
    [11]

Solutions

  1. A = R7000
    i = 0.15
           4
    n =3 × 4
    P =?
    7000 = P( 1  + 0,15)3×4 
                             4
    7000 = P(1,555454331) ………… Divide both sides by 1,555454331
    P = R4500,29 (3)
  2. A = P (1 + i)n substitute for A, P and i
    23 000 = 1 570(1 + 0,12)n simplify and divide
    23000 = (1,12)n keep the number on your calculator without rounding
    1570
    14,6496… = (1,12)n use log laws
    n = log1,12 14,6496… Use the log keys on your calculator.
    n = 23,69 years n ≈ 24 years to the nearest year(4)
  3. A = 2860
    P = 2000
    i = ?
    n = 18
    A = P (1 + i)n
    2000( 1  + i )18 = 2860
                   12
    ( 1  + i )18 = 2860
           12        2000
    1 +  i = 18√1.43
         12
      i    = 0,020069541
    12
    i = 0,020069541... 
    i =0,2408344924 × 100
    i = 24,08% (4)
    [11] 

Activity 3
The value of a piece of machinery depreciates from R10 000 to R 5 000 in 4 years. What is the rate of depreciation, correct to two decimal places, if calculated on the:

  1. Straight line method (i.e. simple depreciation) (3)
  2. Reducing balance (i.e. compound depreciation) (3)
    [6]

Solutions

  1. A = 5 000 P = 10 000 n = 4
    i =? Note: A is less than P
    Straight line method:
    A = P(1 – ni)
    5 000 = 10 000 (1 – 4i) 
     5000  = (1 − 4i) 
    10000
    0,5 – 1 = – 4i
    -0,5 = i
     -4
    0,125 = i
    i =12,5% (3)
  2. Reducing balance:
    A = P (1 – i)n
    5 000 = 10 000(1 – i)4 
     5000  = (1 − i)4
    10000
    0,5 = (1 – i)4
    4√0,5 = 1 – i
    i = 1 – 0,8408…
    i = 0,1591035…
    i = 15,9% (3)
    [6] 

Activity 4

  1. Khosi wants to invest R5 000 for 3 years. Which is the better investment for her if the interest is 10,5% p.a compounded quarterly or 10,5% p.a. compounded monthly? (7)
  2. Convert a nominal interest rate of 9% per annum compounded semi-annually to the effective annual interest rate. (2)
    [9]

Solutions

  1. First option: A = ? P = R5 000 i = 0,105  n = 3 × 4
                                                            4
    A = P (1 + i)n
    A = 5 000 ( 1 + 0,105)3×4 Use a calculator to work out the whole answer.
                                4
    A = R6823,51
    Second option: A = ? P = R5 000 i = 0,105  n = 3 × 12
                                                                12
    A = P (1 + i)n
    A = 5000 ( 1 +  0,105)3 x 12 Use a calculator to work out the whole answer.
                              12
    A = R6 841,923
    ∴10,5% compounded monthly gives Khosi a better interest on her investment. (7)
  2. 1 + ieffective = ( 1 + inominal)k k if k is the number of times per year the interest is calculated.
                                          2
    1 + i = ( 1 +  0,09)2
                          2
    1 + i =1,092025 …
    i = 0,092025
    ∴ 9,20% is the effective annual interest rate. (2)
    [9] 

Activity 5
Mr. Sithole invests R50 000 in an account which offers 8% p.a. interest compounded quarterly for the first 18 months. The interest then changes to 6% p.a. compounded monthly. Two years after the money is invested, R10 000 is withdrawn. How much will be in the account after 4 years?
[5]

Solution
Draw a timeline. The total length of time is 4 years.
2
METHOD 1
DEPOSIT for the period of 4 years
A = 50000 ( 1 + 0.08)1.5×4 ( 1 +  0.06)2.5×12  − 10000 (1 +  0.06)2×12
                           4                        12                                    12
=R54 124,66 

OR
METHOD 2

First 18 months (18 =1,5 years):
                           12
P = R50 000 i = 8% compounded quarterly = 0,08 n = 1,5 years × 4
                                                                          4
A = 50000 ( 1 + 0,08)1,5×4 = R56 308,12096
                           4
Next 6 months (0,5 years):
P = R56 308,12096 i = 6% compounded monthly = 0,06 n = 0,5 × 12
                                                                                   12
A = 56308,12096 ( 1 + 0,06)0,5×12 
                                      12
= R58 018,62143
R10 000 withdrawn, so R48 018,62143 remains as the new P value.
Next 2 years
P = 48 018,62134 i = 6% compounded monthly = 0,06 n = 2 × 12
                                                                                 12
A = 48018,62134 ( 1 + 0,06)2×12
= R54 124,66 [5] 

Deposit of 50 000 with two different interest for the whole period minus the withdrawal with interest for the remaining period

Activity 6: Interpret a graph
1. Ntsako invests R50 000 at 14% p.a. compounded annually. Liz saves R50 000 at 13,7% p.a. compounded monthly.

  1. Who has the most money at the end of 20 years?
  2. Calculate the difference in their investments after 20 years.
    [6]

Solutions

    1. Ntsako: A = 50 000(1 + 0,14) 20 = R687 174,49
      Liz: A = 50000 ( 1 +  0,137)20×12 
                                        12
       = R762421,9984 = R762 422,00
      Liz has the most money. 
    2. The difference is R762 422,00 – R687 174,49 = R75 247,51.
      [6] 

Activity 7

  1. In order to buy a car, Zack takes out a loan of R25 000 from the bank. The bank charges an annual interest rate of 11% compounded monthly. The installments start a month after he has received the money from the bank.
    1. Calculate his monthly installments if he has to pay back the loan over a period of 5 years.
    2. Calculate the outstanding balance of his loan after two years (immediately after the 24thinstalment). (8)
  2. Jill negotiates a loan of R300 000 with a bank which has to be repaid by means of monthly payments of R5 000 and a final payment which is less than R5 000.The repayments start one month after the granting of the loan. Interest is fixed at 18% per annum, compounded monthly
    1. Determine the number of payments required to settle the loan.
    2. Calculate the balance outstanding after Jill has paid the last R5 000.
    3. Calculate the value of the final payment made by Jill to settle the loan.
    4. Calculate the total amount Jill repaid to the bank. (13)
      [21]

Solutions

    1. P = R25 000; i = 11% monthly = 0,11 x i s the monthly installment
                                                                   12
      n = 5 × 12 = 60
      5
      His monthly installment will be R543,56 (to the nearest cent)
    2. 5 years × 12 months = 60 months. He still has to pay for 60 – 24 = 36 months.
      6
      The outstanding balance after two years will be R16 602,97
      (to the nearest cent).(8)
    1. P = 300 000 x = 5 000 i = 0,18 = 0,015 3 n = ?
                                                 12
      P = x [ 1 – (1 + i) –n ]
                        i
      300 000 = 5000 [ 1 – (1 + 0,015) –n ]
                                   0.015
      300 000 × 0,015 = 5 000 [1 – (1,015)–n]
      4500 – 1 = – (1,015)–n
      5000
      – (1,015)–n = –0,1
      – n =  log 0,1 
              log 1.015
      n =154,65
      ∴ Number of payments = 155
    2. 7
    3. Amount paid in last month
      = 3230,50 ( 1 + 0,18)
                                 12
      = R3278, 96
    4. Total repaid = (154 × 5000) + 3278,96 = R773278,96 3 (13)
      [21] 

Since n = 154,6541086, the outstanding period to cover the whole loan is 0,6541086
There are 154 equal monthly payments of R5 000 plus the last instalment which is less than R5 000

Activity 8

  1. A farmer buys a tractor for R450 000.
    1. How much will the tractor be worth in 5 years’ time if its value depreciates at 9% per annum on a reducing balance? (3)
    2. After 5 years, the tractor needs to be replaced. During this time, inflation remains constant at 7% per annum. Determine the cost of a new tractor after 5 years. (3)
    3. He plans to sell this tractor at its book value and use the money towards a new tractor. Calculate how much money he will need to put into a Sinking Fund to buy a new tractor in 5 years’ time. (1)
    4. Calculate the value of the monthly payment into the sinking fund if the interest is 8,5% p.a. compounded monthly over the next 5 years. (4)
  2. Timothy buys furniture to the value of R10 000. He borrows the money on 1 February 2010 from a financial institution that charges interest at a rate of 9,5% p.a. compounded monthly. Timothy agrees to pay monthly installments of R450. The agreement of the loan allows Timothy to start paying these equal monthly installments from 1 August 2010.
    1. Calculate the total amount owing to the financial institution on 1 July 2010. (2)
    2. How many months will it take to pay back the loan? (6)
    3. What is the balance of the loan immediately after Timothy has made the 25th payment? (4)
  3. Calculate how many years it will take for an investment to treble (becomes three times as big) if it is invested at 12% per annum compounded half-yearly. (5)
    [28]

Solutions

    1. Use compound depreciation with P = R450 000, i = 0,09,
      n = 5 years.
      A = P (1 – i)n
      A = 450 000 (1 – 0,09)5 
      A = 280 814,4653
      The tractor will be worth R 280 814,47 in 5 years’ time. 
      (This is what its ‘book value’ or ‘scrap value’ will be in 5 years’ time) (3)
    2. Use compound interest for inflation with P = R450 000, i = 0,07,
      n = 5 years.
      A = P(1 + i)n
      A = 450 000 (1 + 0,07)5 
      A = 631 148.2788
      A new tractor will cost R631 148,29 in 5 years’ time. (3) 
    3. Cost of new tractor – book value of old tractor)
      = R631 148,29 – R280 814,47
      = R350 333,82 in a Sinking Fund.
    4. Use the Future value formula and solve for x.
      F = R350 333,82x is the monthly installment
      i = 8,5% compounded monthly =0.085/12 n = 5 × 12 = 60 months
      8
      The monthly payment into the sinking fund over the next 5 yearsThe monthly payment into the sinking fund over the next 5 yearsneeds to be R4 706,10 (rounded off to the nearest cent)(4)
  2.  
    1. A = 10000 ( 1 +A = 10000 ( 1 + 0.095/12)5
      = R10 402,15 (2)

    2.  9
    3. Balance outstanding after 25 months
      = 25, 6315128204… – 25
      = 0, 6315128204 
      10
  3. Let x be the P, the investment in rand.
    So the final amount A will be three times as much: 3x Rand.
    i = 12% compounded half-yearly (twice a year) = 0,12
                                                                                     2
    A = P (1 + i)n
    3x = x ( 1 + 0,12)n×2 
                         2
    3x = (1,06)2n
     x
    3 = (1,06)2n Use logs to find n
    2n = log1,06 3 
    2n = 18,85
    n = 9,42708834…
    It will take more than 9 years, so we say that the answer is 10 years.
    It will take 10 years for an investment to treble if interest of 12% is compounded half-yearly. (5)
    [28]
Last modified on Monday, 30 August 2021 11:45
Published in Grade 12 Mathematics Study Guide and Notes

Related items

More in this category: « TRIG FUNCTIONS QUESTIONS AND ANSWERS GRADE 12 CALCULUS QUESTIONS AND ANSWERS GRADE 12 »
back to top