ElimuZA Access to Education
CALCULUS QUESTIONS AND ANSWERS GRADE 12
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupActivity 1
- Determine the average gradient of the graph of y = 5x2 – 4 between x = –4 and x = –1
- Is the function increasing or decreasing between x = –4 and x = –1? (3)
- Determine the average gradient of the graph of y = 5x2 –4 between:
- x = 1 and x = 3
- x = 2 and x = 3
- x = 2,5 and x = 3
- x = 2,99 and x = 3 (8)
- Calculate the average gradient of the curve f(x) = x(x + 3) between x = 5 and x = 3.
- What can you deduce about the function f between x = 5 and x = 3? (3)
[14]
Solutions
|
Use the equation of the curve y = 5x2 –4 to calculate the y-values.
Use the y2 − y1 formula to calculate the gradient.
x2 - x1
Calculate the gradient of a curve?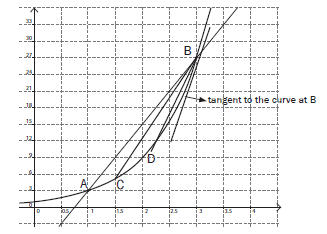
- The average gradient between two points on a curve is equal to the gradient of the straight line through the points. So the average gradient of curve AB is 12.
- As the two points are moved closer together, the average gradient approaches the gradient of the curve which is also the gradient of the tangent to the curve at that point. So the gradient of the curve AB at point B is 30.
- Remember that the tangent is a line that touches a curve at one point only.
- The average gradient tells us whether the graph is increasing or decreasing between those points.
- If the function is decreasing between two points, the average gradient will be negative.
- If the function is increasing between two points, the average gradient will be positive.
Activity 2
- Determine f ´(x) from first principles if f(x) = 5x2 – 4x + 2 (6)
- Determine f ´(x) from first principles if f(x) = 2/x (6)
[12]
Solutions
(6) |
Activity 3
- Evaluate Dx[ (x3 – 3)2]
- Find f ´(x) if f(x)= 3√x
- Find d 3√x5
dx - Differentiate f(x) if f(x) = √x4
- Find f ´(x) if f(x) = √16x3
[11]
 Rewrite terms which are ‘fractions’ where x is part of the denominator, 1/xn as x−n so that you can use the rule: if f(x) = xn then f ´(x) = nxn–1
Rewrite terms which are ‘fractions’ where x is part of the denominator, 1/xn as x−n so that you can use the rule: if f(x) = xn then f ´(x) = nxn–1
e.g.6
Find f ´(x) if f(x) = 3x 2
4x3
| Solution f(x) = 3x2 = 3 x−1 4x3 4 So f ´(x) = − 3 x−2 = − 3 4 4x2 |
Activity 4
- Determine, using the rules of differentiation: dy if y = √x - 1 (3)
dx 2 6x3 - Evaluate dy if y = 4 - x 3
dx √x 9 (3) - Determine Dx [ 6x + 5 ] (4)
3x2
[10]
Solutions
|
Activity 5
- f(x) = − x3 − x2 + x + 10
- Write down the coordinates of the y-intercept of f
- Show that (2; 0) is the only x-intercept.
- Calculate the coordinates of the turning points of f
- Sketch the graph of f. Show all intercepts with axes and all turning points.
- Determine the point of inflection. (17)
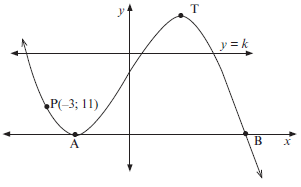
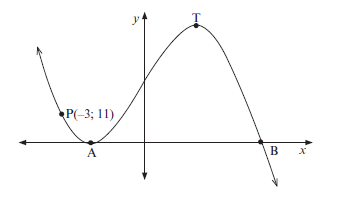
- Sketched below is the graph of g(x) = –2x3 – 3x2 + 12x + 20 = –(2x – 5)(x + 2)2. A and T are turning points of g. A and B are the x-intercepts of g. P(–3; 11) is a point on the graph.

- Determine the x-coordinate of T.
- Determine the equation of the tangent to g at P(–3; 11) in the form y = …
- Determine the value(s) of k for which –2x3 – 3x2 + 12x + 20 = k has three distinct roots.
- Determine the x-coordinate of the point of inflection. (14)
[31]
Solutions
|
Activity 6
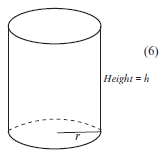
- A drinking glass, in the shape of a cylinder (shown here), must hold 200 ml of liquid when full.
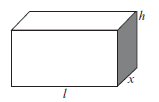
Find the value of r for which the total surface area of the glass is a minimum. - A rectangular box is constructed in such a way that the length (l) of the base is three times as long as its width. The material used to construct the top and the bottom of the box costs R100 per square metre. The material used to construct the sides of the box costs R50 per square metre. The box must have a volume of 9 m3. Let the width of the box be x metres.

2.1 Determine an expression for the height (h) of the box in terms of x.
2.2 Show that the cost to construct the box can be expressed as
C = 1200 + 600x2
x
2.3 Calculate the width of the box (that is the value of x) if the cost is to be a minimum. - A tourist travels in a car over a mountainous pass during his trip.
The height above sea level of the car, after t minutes, is given as s(t) = 5t3 − 65t2 + 200t + 100 metres. The journey lasts 8 minutes.
3.1 How high is the car above sea level when it starts its journey on the mountainous pass?
3.2 Calculate the car’s rate of change of height above sea level with respect to time, 4 minutes after starting the journey on the mountainous pass.
3.3 Interpret your answer to QUESTION 3.2.
3.4 How many minutes after the journey has started will the rate of change of height with respect to time be a minimum? (3)
[26]
Solutions
|
Published in Grade 12 Mathematics Study Guide and Notes

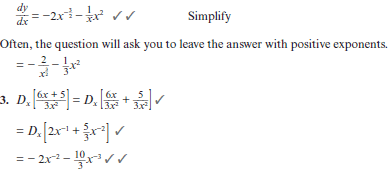
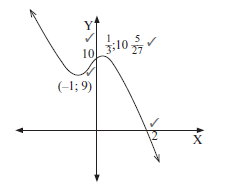 (4)
(4)