ANALYTICAL GEOMETRY QUESTIONS AND ANSWERS GRADE 12
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupActivity 1
- For a line passing through the two points A(6; 6) and B(3; 2), calculate the length of AB. (3)
- If PQ = 5 units; P (5; t) and Q (1; –3) determine the possible value(s) of t. (3)
[6]
Solutions
|
3. The midpoint of a line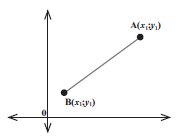
If you know the coordinates of the two endpoints of a line, you can find the point that is halfway between them. This is called the midpoint.
The midpoint of a line has the coordinates
( x1 + x2;y1 + y2)
2 2
where (x1; y1) and (x2; y2) are the endpoints of the line.
e.g.3
For a line passing through the two points A(6; 6) and B(3; 2), find the
coordinates of the midpoint of AB.
Midpoint of AB = ( x1 + x2;y1 + y2)
2 2
= (6 + 3 ; 6 + 2) = (4½ ;4)
2 2
So the midpoint has the coordinates (4½ ;4)
e.g.4
The coordinates of the midpoint of the line AB are (1;-4). Find the coordinates of A if the coordinates of B are (4;-3).
When midpoint is given:
x as the midpoint of AB = xA + xB and y as midpoint of AB = yA + yB
2 2
1 = xA + 4 and –4 = yA − 3
2 2
2 = xA + 4 and –8 = yA − 3
–2 = xA and –5 = yA
Coordinates of A are (-2;-5)
Activity 2
K (–1; –6) and L (5; 4) are two coordinates on the same straight line. Determine the coordinates of the midpoint. (2)
If M (–1; 4) is the midpoint of line segment AB, and the coordinates of A (3;6) are given, find the coordinates of the endpoint B. (3)
[5]
Solutions
We can use coordinate geometry to identify the properties of geometric |
Activity 3
A. (–4; 7), B (4; 5), C (0; –1) and D (a; b) are the vertices of parallelogram ABCD.
- Draw the parallelogram on squared paper. (2)
- Find the midpoint of the diagonal AC. (2)
- Use the information that you have to find the coordinates of point D. (3)
[7]
Solutions
|
Activity 4
- Determine the equation of the straight line that passes through the points P(1; 2) and Q(3; 8) in the form y = .... (3)
- Line AB is perpendicular to CD, which has a gradient of –2. The point (3; 4) lies on AB. Determine the equation of line AB. (2)
[5]
Solutions
|
Activity 5
Give your answers correct to two decimal places.
- Line AB is perpendicular to CD, which has a gradient of –4.
Find the inclination θ of AB. (2) - Determine the inclination of the straight line that passes through the points
P (–6; 2) and Q (3; 10). (2) - Given the points A (–2; –1), B (5; 6) and C (7; –2), calculate the size of ABC . (6)
[10]
Solutions
|
Activity 6
- For a line passing through the two points A(6; 6) and B(3; 2):
1.1 Calculate the length of AB.
1.2 Find the coordinates of the midpoint of AB.
1.3 Calculate the angle of inclination of the line.
1.4 Determine the equation of the line passing through A and B.
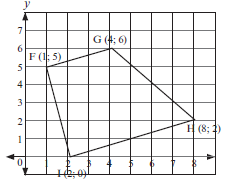
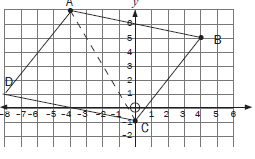
1.5 Determine the equation of a line GH perpendicular to AB passing through the midpoint of AB. (11) - F, G, H and I are the vertices of a quadrilateral shown below.
What kind of quadrilateral is FGHI? (5)
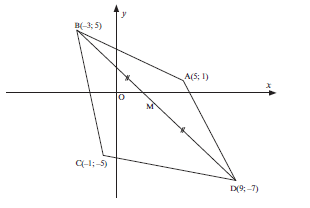
- ABCD is a quadrilateral with vertices A(5 ; 1), B(−3 ; 5), C(−1 ; −5) and D(9 ; −7).

3.1 Calculate the gradient of AC. (2)
3.2 Determine the equation of AC in the form y = … (3)
3.3 Hence, or otherwise, show that the midpoint M of BD lies on AC. (3)
3.4 Show that AMB = 90°. (2)
3.5 Calculate the area of ∆ ABC. (5)
[31]
Solutions
|
Activity 7
- Determine the coordinates of the centre and the length of the radius if a circle has the equation: x2– 2x + y2+ 10y = –14 (3)
- Determine the equation of a circle with centre C(–1; –2) and passing through the point B(1; –6). (3)
[6]
Solutions
|
Activity 8
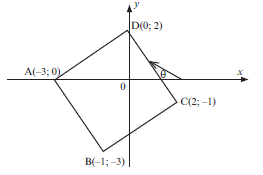
- ABCD is a quadrilateral with vertices A(–3; 0), B(–1; –3), C(2; –1) and D(0; 2).

1.1 Determine the coordinates of M, the midpoint of AC. (2)
1.2 Show that AC and BD bisect each other. (3)
1.3 Prove that A| D^ C = 90°. (4)
1.4 Show that ABCD is a square. (4)
1.5 Determine the size of θ, the angle of inclination of DC, correct to ONE decimal place. (3)
1.6 Does C lie inside or outside the circle with centre (0; 0) and radius 2? Justify your answer. (2)
[18]
| Solutions 1.1 Midpoint M of AC: 2 − 3; − 1 + 0 = ( − ½ ; -½) (2) 2 2 1.2 Midpoint M of BD: ( −1 + 0; − 3 + 2) = ( −½;-½) 2 2 ∴ So the midpoint of AC and the midpoint of BD are the same point, so they bisect each other.(3) 1.3 mAD= 2 − 0 = 2 and mDC= − 1 − 2 = −3 0-(0-3) 3 2-0 2 mAD × mDC = 2 × −3 = –1 3 2 1 ∴AD ⊥ DC ∴ADC = 90° (4) 1.4Here is one possible answer: The diagonals AC and BD bisect each other (proved in 1.2) ADC = 90° (proved in 1.3) AD2 = (2 – 0)2 + (0 – (–3))2 = 4 + 9 = 13
CD2 = (– 1 – 2)2 + (2 – 0)2 = 9 + 4 = 13 CD = √13 So adjacent sides are equal in length ∴ ABCD is a square. (4) 1.5 tan θ = mDC = − 1 − 2 = −3 2 - 0 2 θ = –56,3099324... + 180° θ = 123,7° (3) 1.6 OC2 = (2 – 0)2 + (– 1 – 0)2 OC2= 4 + 1 = 5 OC = √5 This is longer than the radius of 2 of the given circle, so C(2; –1) lies outside the circle 3. (2) [18] |
2. O is the centre of the circle in the figure below. P(x; y) and Q(12; 5) are two points on the circle. POQ is a straight line. The point R(t; –1) lies on the tangent to the circle at Q.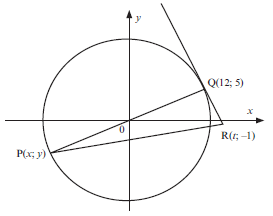
2.1 Determine the equation of the circle. (3)
2.2 Determine the equation of the straight line through P and Q. (2)
2.3 Determine x and y, the coordinates of P. (4)
2.4 Show that the gradient of QR is -12/5 (2)
2.5 Determine the equation of the tangent QR in the form y = … (3)
2.6 Calculate the value of t. (2)
2.7 Determine an equation of the circle with centre Q(12; 5) and passing through the origin. (3)
[19]
| Solutions The centre is at the origin, so x2 + y2 = r2. 2.1 OQ2 = (5)2 + (12)2 = 25 + 144 = 169 So the equation of the circle is x2 + y2 = 169 (3) 2.2 mPQ = mOQ = 0 – 5 = 5 0 - 12 12 PQ has y-intercept of 0. 3 (2) y = 5/12 x 2.3 By symmetry, P is the point (–12; –5). OR Substitute y = 5/12 x into x2 + y2 = 169 x2 + (5/12 x )2 = 169 x2 + 25/144 x2 = 169 144x2 + 25x2 = 169 × 144 169x2 = 24 336 x2 = 144 x = 12 or x = –12 x = –12 according to given diagram y = 5/12 x = 5/12 × (–12) = –5 (4) So P is the point (–12; –5). 2.4 tangent ⊥ radius so QR ⊥ PQ mPQ = 0 − 5 = 5 0 -12 12 ∴mQR = − 12/5 (2) 2.5 y = − 12/5 x + c OR y – y1 = − 12/5 (x – x1) Substitute Q(12; 5) into equation to find c: 5 = − 12/5 (12) + c y – 5 = − 12/5 (x – 12) 5 + 144/5 = c y =− 12/5 x + 144 + 5 c = 169/5 y = − 12/5 x + 169/5 y = − 12/5 x + 169/5(3) 2.6 R(t; –1) lies on line with equation y = − 12/5 x + 169/5 ∴ –1 = − 12/5 t + 169/5 –5 = –12t + 169 12t = 174 t = 14,5 (2) 2.7 OQ2 = (x – 12)2 + (y – 5)2 Q(12; 5) is centre of circle Substitute (0; 0) into equation: OQ2 = (0 – 12)2 + (0 – 5)2 OQ2 = 144 + 25 = 169 ∴ (x – 12)2 + (y – 5)2 = 169 (3) [19] |
 (2)
(2)