TRIGONOMETRY:SINE, COSINE AND AREA RULES QUESTIONS AND ANSWERS GRADE 12

More in this category: « TRIGONOMETRY QUESTIONS AND ANSWERS GRADE 12 EUCLIDEAN GEOMETRY QUESTIONS AND ANSWERS GRADE 12 »
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

Activity 1
In triangle ABC, ^B = 37° and AC = 16 cm. ^C = 90°. Calculate the length of AB and BC (correct to one decimal place). (3)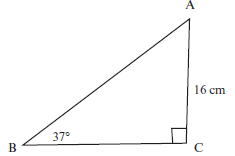
1

Solution
To calculate the length of AB, use 37° as the reference angle, then
AC = 16 cm is the opposite side and AB is the hypotenuse. Use the sine ratio.
sin 37° = opp =16
               hyp   AB
AB sin 37° = 16
AB =   16   = 26,6 cm 
        sin37° 
To find the length of BC, you can use
cos 37° = adj = BC/26.6
                hyp
26,6 cos 37° = BC 
BC = 21,2 cm (to one decimal place) 
You can also use Pythagoras’ theorem:
AB2 = AC2 + BC2 [3]
[3] 


Activity 2
In triangle PQR, PQ = 12,3 m and PR = 13 m. Calculate the size of ^Q . (2)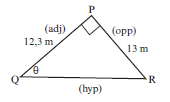
2
[2]

Solution
Use PQ and PR.
tan θ = opp = 13  
                     12.3
θ = tan–1 (13/12.3) = 46,58° [2] 

Activity 3
Solve ∆XYZ in which z = 7,3 m, ^X = 43° and ^Y = 96°. Give your solutions correct to 3 decimal places. (4)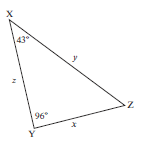
12
[4]

Solution
The angle opposite the known side is not given, but you can work it out.
^Z = 180° – (43° + 96°) (sum angles of ∆)
^Z = 41° 
To find y:       y      = 7,3 
                 sin 96°   sin41° 
y = 7,3 sin 96° 
          sin41° 
y = 11,066 m 
Using the sine rule again to find x:
   x     = 7,3  
sin43°  sin41° 
x = 7,3 sin 43° 
          sin41° 
x = 7,589 m 
[4] 

Activity 4
1. PQRS is a trapezium with PQ // SR, PQ = PS, SR = 10 cm,
QR = 7 cm, ^R = 63°.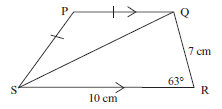
17
Calculate:

  1. SQ (2)
  2. PS (6)
  3. area of quadrilateral PQRS. (correct to 2 decimal places) (5)
    [13]

Solutions

  1. In ∆ QSR, you know two sides and the included angle, so use the cosine rule.
    SQ² = 7² + 10² – 2(7)(10)cos 63° 
    SQ² = 85,44… find the square root
    SQ = 9,24 cm  (2)
  2. In Δ PQS, you know that PQ = PS and you worked out that SQ = 9,24 cm.
    Think about the question first
    If you can find ^P then you can use the sine rule to find PS.
    To find ^P , you need to first find PQS or PSQ .
    PQ S = PSQ (alternate angles, PQ // SR)
    Now can you work out a value for QSR ?
    In ∆QSR, you know three sides and ^R .
    So it is easiest to use the sine rule to find QSR .
    sin QSR = sin 63° 
         7            9,24
    sin QSR = 7 sin 63° = 0.675004
                          9,24  
    ∴ QSR = 42,45° 
    PQS= QSR = 42,45° (alternate angles, PQ // SR)
    PQS= PSQ = 42,45° (base angles of isosceles ∆)
    ∴ ^P = (180° – (42,45° + 42,45°) 
    = 95,1°  (sum angles in ∆)
    Now we can find PS using the sine rule and ^P .
    In ∆PQS     PS     =    9,24   
                 sin42.45°     sin95,1
    PS =  9,24 sin 42,45°
                   sin95.1
    PS = 6,26 cm (6) 
  3. To find the areas of PQRS, find the area of the two triangles and add them together.
    To find the area of ∆PQS, use ^P = 95,1° and PS = PQ = 6,26 cm.
    Area ∆PQS =  ½ qs sin P 
    Area ∆PQS = ½ (6,26)(6,26)sin95,1°
    Area ∆PQS = 19,52 m² 
    To find the area of ∆RQS, use ^R = 63°, QR = 7 cm and SR = 10 cm.
    Area ∆RQS = ½ (7)(10)sin63 
    Area ∆RQS = 31,19 m² 
    ∴Area PQRS = 19,52 + 31,19 = 50,71 m²  (5)
    [13]

When solving triangles, start with the triangle which has most information (i.e. triangle with three sides or two sides and an angle or two angles and a side given)

Activity 5
In the diagram alongside, AC = 7 cm,
DC = 3 cm, AB = AD, DCA = 60°,
DAB = β and ABD  = θ.
Show that BD = √37  sin β
                              sinθ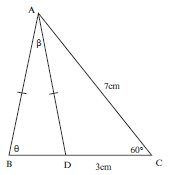
18
[3] 

Solution
AD2  =  AC2  +  CD2  − 2AC.CD cos 60 ° = (7)2 + (3)2 – 2 × 7 × 3 × 0,5
AD2 =58 – 21
AD2 = 37
AD = √37 P
Applying sine rule:
 BD  =  AD ⇒ BD = AD sin β but AD = √37
sinβ    sinθ                 sinθ 
∴BD = √37 sin β
               sinθ
[3] 


Activity 6

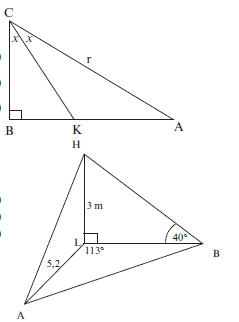
  1. In the diagram alongside, ABC is a right angled triangle. KC is the bisector of ACB. AC = r units and BCK = x
    1.1 Write down AB in terms of x (2)
    1.2 Give the size of AKC in terms of x (2)
    1.3 If it is given that AK =  2  , calculate the value of x (7)
                                    AB     3 
    19
  2. A, B and L are points in the same horizontal plane, HL is a vertical pole of length 3 metres,
    AL = 5,2 m, the angle ALB = 113° and the angle of elevation of H from B is 40°.
    2.1 Calculate the length of LB. (3)
    2.2 Hence, or otherwise, calculate the length of AB. (3)
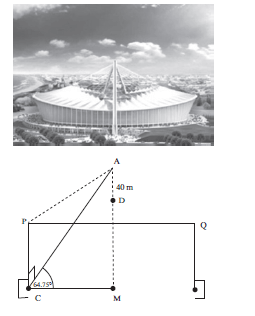
    2.3 Determine the area of ∆ABL. (3)
  3. The angle of elevation from a point C on the ground, at the centre of the goalpost, to the highest point A of the arc, directly above the centre of the Moses Mabhida soccer stadium, is 64,75°. The soccer pitch is 100 metres long and 64 metres wide as prescribed by FIFA for world cup stadiums. Also AC ⊥ PC.
    In the figure below PQ = 100 metres and PC = 32 metres
    3.1 Determine AC (2)
    3.2 Calculate PAC (2)
    3.3 A camera is placed at D, 40 m directly below point A, calculate the distance from D to C (4)
    20
    [28]
Solutions
1.1 sin 2x = AB  ∴ AB = r sin 2x (2)
                    r
1.2 AKC = 90° + x [ext. angle of ∆CBK]  (2)
1.3  AK   =         r        ∴ AK =  r sinx
     sin x    sin(90° + x)             cos x 
         r sin x
AK =  cos x  =            r sin x          =       1       =  2 
AB   r sin 2x    r cos x.2 cos x sin x    2 cos2x      3
∴ cos2x =  3/4
cos x =  √3/2
Hence x =  30º (7)
2.1 In ∆HLB, tan 40° = 3 
                                   LB
[∆HLB is right-angled, so use a trig ratio]
LB =     3     
         tan40º
LB = 3,5752… ≈ 3,58 metres (3)
2.2 In ∆ABL,
[ΔABL not right-angled. You have two sides and included angle, so use the Cosine Rule]
AB2 = AL2 + BL2 – 2(AL)(BL).cos L 
AB2 = (5,2)2 + (3,58)2 – 2(5,2)(3,58).cos 113° 
AB2 = 54,40410… m2
AB = 7,38 m (3)
2.3 Area ∆ABL = ½  AL × BL × sin ALB 
= ½ (5,2) × (3,58) × sin 113° 
= 8,56805… 
≈ 8,57 m2 (3)
3.1 cos 64,750° = CM ∴ AC =      CM      =      50m     = 117,21 (2)
                             AC             cos64.75°    0.426569
3.2 tanPAC =  PC
                       AC
PAC = tan−1 (32/AC)
= 15,27° (2)
3.3 DC2  = AC2  + AD2  − 2AC.ADcos(90°  − 64,75°) 
DC2  = (117,21 )2  + (40)2  − 2(117,21).40cos(25,25°)
= 6857,289 
DC = 82,81m  (4)
[28] 
Last modified on Thursday, 02 September 2021 07:31
Published in Grade 12 Mathematics Study Guide and Notes

Related items

More in this category: « TRIGONOMETRY QUESTIONS AND ANSWERS GRADE 12 EUCLIDEAN GEOMETRY QUESTIONS AND ANSWERS GRADE 12 »
back to top