Activity 1

1. Determine the value of x, in the diagram alongside, if PQ ∣∣ BC. (4)

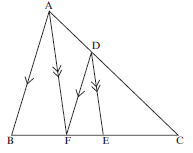
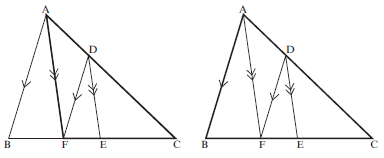
   Solution AP = AQ (PQ ∣∣ BC, prop theorem)  PB    QC ∴ 5/3 = 4/x ∴ 5x = (3)(4) ∴ x = 12/5 = 2,4 cm 3 [4]

2. In ∆ABC, AB ∣∣ FD; AF ∣∣ DE and FE : EC = 3 : 4.
   Determine EC : BF (7) 
   
   NOTE:
   3 : 4 does not mean that
   FE = 3 and EC = 4.
   For any a, we can say that
   FE = 3a and EC = 4a
   For every 3 of a in FE, there is
   4 of a in EC.

   Solution Work with two different triangles: ∆ACF and  ABC In ∆ACF: AD = FE (AF ∣∣ DE, prop intercept theorem)  DC   EC In ∆ABC: AD = BF (AB ∣∣ FD, prop intercept theorem) DC    FC ∴ FE = BF(both = AD)    EC   FC             DC  FE = 3a and BF = BF  EC    4a       FC     7a ∴ 3a = BF    4a    7a ∴ BF = 3(7a/4) = 21a____4 ∴ EC   = 4a ÷ 21a/4    BF = 4a ×  4       1    21a = 16     21 ∴ EC : BF = 16 : 21 [7]

3. Determine the value of x if PQ ∣∣ BC. (4)

   Solution AP = AQ (prop theorem , PQ ∣∣ BC) PB    QC 5/3 =  4/x 5x = (3) (4) x = 12/5 = 2,4cm  [4]

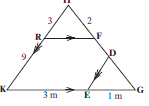
4. In the diagram, RF ∣∣ KG , ED ∣∣ KH,
   

   RH = 3 units, RK = 9 units, HF = 2 units. GE: EK = 1:3
   
   Calculate (stating reasons) the lengths of:
   4.1 FG
   4.2 FD (8)

   Solutions 4.1 In ∆HKG FG = 9 S (line ∣∣ one side of a ∆) 3 R or (RF ∣∣ KG)   2     3 FG = 6 units S (3) 4.2 GD = GE = ¼ S (line ∣∣ one side of a ∆) 3 R or (ED ∣∣ KH)       GH    GK     GD =  ¼ .GH GD = ¼ .(8) S GD = 2 S  ∴ FD = 6 − 2 = 4units 3 R OR In ∆HKG, HK ∣∣ DE GD = EG = 1/3 S DH    EK (line ∣∣ one side of a ∆) R or (proportional theorem, HK//DE ) 6 − FD = 1/3 S 2 + FD 18 − 3FD = 2 + FD ∴ FD = 4 units (5) [8]

Activity 2

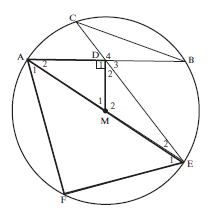
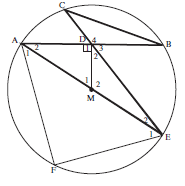
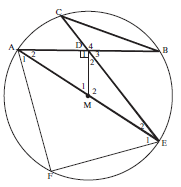
1. Diameter AME of circle with centre M bisects FAB.
   MD is perpendicular to the chord AB.
   ED produced meets the circle at C, and CB is joined.
   
   
   1. Prove ∆AEF ||| ∆AMD (5)
   2. Hence, find the numerical value of AF. (5)
                                                             AD 
   3. Prove ∆ CDB ||| ∆ADE (4)
   4. Prove AD² = CD. DE (3)
      [17]

      Solution a) F = 90° (∠ in semi-circle)  ^D1 = 90° (given MD ⊥ AB)  ∴ ^F = ^D1 In ∆AEF and ∆AMD ^F = ^D1  (proved) ^A1 = ^A2 (AM bisects FAB)  ∴ ^E1 = ^M1 (third ∠ of ∆) ∴ ∆AEF ∣∣∣ ∆AMD (AAA) or ∠∠∠ (5)	Solution b) AE = EF = AF (||| ∆s)     AM    MD   AD AM = ME (radii) ∴ AE = 2AM ∴ 2AM = AF     AM     AD ∴ AF = 2 (5)    AD
      c) In ∆CDB and ∆ADE ^C = ^A2 (∠s in same seg)  ^B = ^E2 (∠s in same seg) ^D4 = ^D1 + ^D2 (opp ∠) ∴ ∆CDB ||| ∆ADE (AAA) (4)	Solution d) CD = DB  (III ∆s) AD     DE ∴ CD.DE = AD.DB  But AD = DB (MD ⊥ AB, M is centre)  ∴ CD. DE = AD  ∴ AD2 = CD.DE (3) [17]

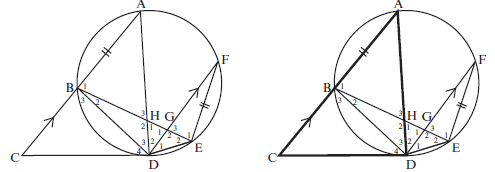
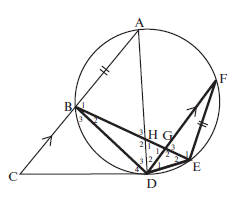
2. CD is a tangent to circle ABDEF at D.
   Chord AB is produced to C. Chord BE cuts chord AD in H and chord FD in G. AC ∣∣ FD and FE = AB
   
   
   1. Prove that ^D₄ = ^D₂ (3)
   2. Prove that ∆BHD ||| ∆FED (5)
   3. Hence AB = FD (3)
                 BH    BD

      Solutions a) ^A = ^D4 (tan-chord thm) ^D2 = ^A (alt ∠s CA ∣∣ DF) ^D4 = ^D2 (3) b) In ∆BHD and ∆FED ^B2 = ^F(∠s in same seg)  ^D3 = ^D1 (equal chords)  ^H2 = ^E2 (third ∠ of Δ) ∴ ∆BHD ||| ∆FED ∠∠∠ (5) c) FE = FD (||| ∆s)    BH    BD But FE = AB (given) ∴ AB = FD (3)    BH    BD [11]

      [11]

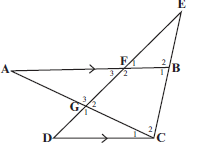
3. In the diagram ∆ABC is such that F is on AB and G is on AC. CB is produced to meet GF produced at E .DGFE is a straight line. BFA ∣∣ CD.
   AB = 20, BC = 10, EF = 8, EB = 5 and FB = 6.
   
   3.1 Determine the numerical value of EF (3)
                                                              ED
   3.2 Calculate the length of ED (2)
   3.3 Complete, without stating the reasons: ∆EFB III ∆ …. (1)
   3.4 Hence, calculate the length of DC (3)
   3.5 Prove that: AF = FG(4)
                           CD    DG 
   [13]

   Solutions BFA ∣∣ CD. AB = 20, BC = 10, EF = 8, EB = 5 and FB = 6 3.1 FB ll CD (Given) EF = EB S (line ∣∣ one side of A) 3 R                                  ED    EC EF = 5 = 1 S (3) ED   15   3 3.2 EF = 1 from 3.1 and EF = 8       ED   3 ∴ 8  = 1    ED   3 ED = 24 S (2) 3.3 ∆EFB ∣∣∣ ∆EDC (1) 3.4 DC = ED (∆EFB ∣∣∣ ∆EDC) R       FB     EF DC = 24 S  6       8 DC = 18 S (3) 3.5 In ∆AFG and ∆CDG ^A = ^C1 (alt ∠s. AF ∣∣ DC) S/R ^G3 = ^G1 (vertically opp ∠s) S/R ^F = ^D (alt ∠s. 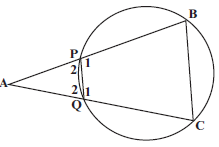AF ∣∣ DC) ∆ AFG III ∆CDG (∠∠∠) R AF = FG (∆AFG ∣∣∣ ∆CDG) 3 R (4) CD    DG  [13]

4. In the diagram, PQCB is a cyclic quadrilateral. Chords BP and CQ are produced to meet at A such that AQ = BC.
   
   4.1 Prove that: ΔAPQ III ΔACB (4)
   4.2 Hence, prove that AQ² = AB.PQ (3)
   [7]

   Solutions 4.1 Proof: In ΔAPQ and ΔACB ^A = ^A (common) S/R ^P2 = ^C S (ext ∠ of a cyclic quad ) 3 R ^P2 = ^ B (sum ∠s of ∆) or ( ext ∠ of cyclic quad ) ∆APQ ∣∣∣ ∆ACB ( ∠.∠.∠) R (4) 4.2 AQ = PQ S (∆APQ ∣∣∣ ∆ACB) S       AB    BC  AQ = PQ S ( AQ = BC ) AB     AQ  AQ2 = AB.PQ (3) [7]