WORK, ENERGY AND POWER - PHYSICAL SCIENCES PAPER 1 STUDY GUIDES AND NOTES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group4.1 Work Summary
- Work is a scalar quantity and therefore does not have a direction.
- The measuring unit of work is Joule. The symbol of Joule is J.
- Net Work is the sum of all work done on an object.
- Net Work is done by a Net Force.
- Positive work is the work done on an object to move it in the direction of the force (or component of the force). Positive work increases the kinetic energy of an object.
- Negative work is the work done by an opposing force. Negative work decreases the kinetic energy of an object.
- Work done by the man is positive.
- Work done by the friction is negative.

You must remember:
- Work is defined as the product of the force parallel to the movement of an object and the displacement of the object.
- Work can be defined Mathematically as: W = F Δx cos θ
- W is the magnitude of work
- F is the magnitude of the applied force
- Δx is the magnitude of the displacement
- θ is the angle between the applied force and the displacement of the object.
- Work-energy theorem: The net work done on an object is equal to the change in the object’s kinetic energy OR work done on an object by a net force is equal to the change in the object’s kinetic energy.
- Work-energy theorem formula: Wnet = ΔK = Kf – Ki
This is just saying that the total work is the the difference between the initial and the final kinetic energy state.
Activity 1
Multiple Choice Questions
Four options are provided as possible answers to the following questions.
Each question has only ONE correct answer. Write only the letter (A–D) next to the question number (1.1 – 1.2).
- An object moves in a straight line on a ROUGH horizontal surface.
If the net work done on the object is zero, then- the object has zero kinetic energy.
- the object moves at constant speed.
- the object moves at constant acceleration.
- there is no frictional force acting on the object. (2)
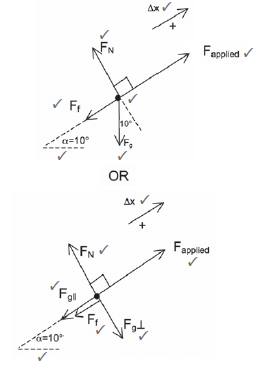
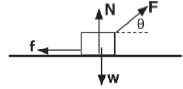
- An object is pulled along a straight horizontal road to the right without being lifted. The force diagram below shows all the forces acting on the object.

Which ONE of the above forces does POSITIVE WORK on the object?- W
- N
- f
- component F (2)
[4]
| Solutions 1. B (2) 2. D (2) [4] |
Activity 2: Work
A 220 N force is applied horizontally to a box of mass 50 kg which rests on a rough horizontal surface and the box moves 10 m. The kinetic friction between the surface and the box is 40 N. Calculate:
- The work done on the box by the applied force. (3)
- The work done on the box by the normal force. (3)
- The work done on the box by the friction. (3)
- The net work done on the box. (3)
- The net force acting on the box. (5)
- The work done on the box by the net force. (3)
[20]
Solutions
|
Activity 3: Work
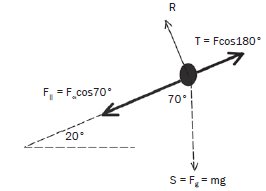
A crateof mass 70 kg slides down a rough incline that makes an angle of 20° with the horizontal, as shown in the diagram below. The crate experiences a constant frictional force of magnitude 190 N during its motion down the incline. The forces acting on the crate are represented by R, S and T.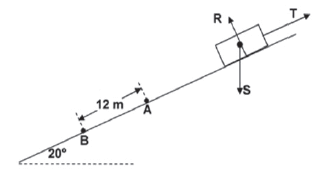
- Label the forces R, S and T. (3)
- The crate passes point A at a speed of 2 m·s–1 and moves a distance of 12 m before reaching point B lower down on the incline. Calculate the net work done on the crate during its motion from point A to point B. (5)
[8]
Solutions
|
HINT:
- Draw a free body diagram and label all the forces.
- Resolve the Force of gravity into its components to determine the applied force acting down the incline.
- To determine the net work apply the formula (W = FΔx⋅cos(180˚)) to both the applied force and the frictional force and add to find the net work done.
Activity 4: Work-energy theorem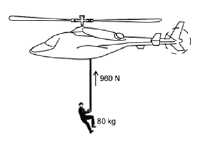
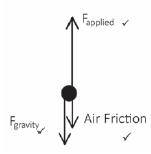
A rescue helicopter is stationary (hovers) above a soldier. The soldier of mass 80 kg is lifted vertically through a height of 20 m by a cable at a CONSTANT SPEED of 4 m·s–1. The tension in the cable is 960 N. Assume that there is no sideways motion during the lift. Air friction is not to be ignored.
- State the work-energy theorem in words. (2)
- Draw a labelled free body diagram showing ALL the forces acting on the soldier while being lifted upwards. (3)
- Write down the name of a non-constant force that acts on the soldier during the upward lift. (1)
- Use the WORK-ENERGY THEOREM to calculate the work done on the soldier by friction after moving through the height of 20 m. (5)
- Identify TWO forces which do negative work. (2)
[13]
Solutions
|
4.2 Energy
Summary
- Energy is a scalar quantity and therefore it does not have a direction
- The measuring unit of energy is called Joule. The symbol of Joule is J.
- The principle of conservation of mechanical energy states that the total mechanical energy (sum of gravitational potential energy and kinetic energy) in an isolated system remains constant. (A system is isolated when the resultant/net external force acting on the system is zero.)
- Solve conservation of energy problems using the equation: Wnc = ΔEk + ΔEp
- The formula Ek = ½ mv2 is used to calculate the kinetic energy.
- The formula Ep = mgH is used to calculate the potential energy.
- The Law of Conservation of Energy states that energy cannot be created or destroyed. Energy can only be transferred from one object to another or transformed from one type of energy to another type.
You must remember:
- Energy is the ability to do work
- A conservative force is defined as a force for which the work done in moving an object between two points is independent of the path taken. Examples are gravitational force, the elastic force in a spring and electrostatic forces (coulomb forces).
- A non-conservative force is defined as a force for which the work done in moving an object between two points depends on the path taken. Examples are frictional force, air resistance, tension in a cable, etc.
Activity 5
Multiple Choice Questions:
Four options are provided as possible answers to the following questions.
Each question has only ONE correct answer. Write only the letter (A–D) next to the question number (5.1 – 5.2).
- The kinetic energy of a car moving at a constant velocity v is K. The velocity of the car changes to 2v. What is the new kinetic energy of the car?
- 0,25 K
- 0,5 K
- 2 K
- 4 K (2)
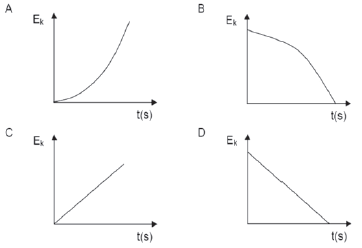
- A stone is dropped from the edge of a cliff. Which ONE of the following graphs best represents the change in kinetic energy of the stone during its fall?
 (2)
(2)
[4]
| Solutions 1. D (2) 2. A (2) [4] |
Activity 6: Work done by Non- Conservative Forces
A box of mass 100 kg slides down a slope. Its velocity increases from 0 m·s−1 at point A to 4 m·s−1 at point B as in the diagram. Calculate the work done by the non-conservative force while it slides from A to B. [4]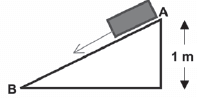
| Solution Wnc = ΔEp + ΔEk = [mghB – mghA] + [½ mvB² − ½ mvA²] = [(100)(9,8)(0) – (100)(9,8)(1)] + [(½ )(100)(4)² − (½ )(100)(0)²] = –980 + 800 = 180 J ∴Wfriction is 180 J [4] |
Remember that a frictional force is an example of a nonconservative force,therefore Wnc = Wf
Activity 7
A toy truck, mass 1,4 kg, moving down an inclined track, has a speed of 0,6 m·s–1 at point P, which is at a height of 1,5 m above the ground level QR. The curved section of the track, PQ, is 1,8 m long. When the truck reaches point Q it has a speed of 3 m·s–1. There is friction between the track and the truck.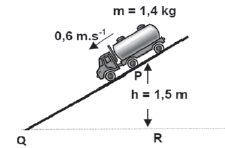
- State the principle of conservation of mechanical energy (2)
- Is mechanical energy conserved? Explain. (2)
- Assume that the average frictional force between the track and the truck is constant along PQ and calculate the average frictional force experienced by the truck as it moves along PQ. (6)
[10]
Solutions
|
- Use the formula Wnet = ΔEK + ΔEp to calculate the work done by the non-conservative force (friction).
- Use the work done by the non-conservative force to calculate friction.
- Remember, Work is a scalar, it does not have a direction and therefore do not leave your answer in a negative form.
4.3 Power
Summary
Power is the rate at which work is done or energy is transferred (or converted).
- Power is an indication of the rate at which (how fast) work is done or energy is transferred or transformed and is a scalar quantity.
You must remember:
- The unit of Power is the watt
- The symbol of watt is W.
- The formula P = W is used to calculate power, where P is power, W is work and Δt is the change in time.
Δt - Average power can be calculated by applying the formula Pav = FVav ,where Pav is the average power, F is the force or net force and Vav is the average velocity or average speed.
Activity 8
Multiple Choice Questions:
Four options are provided as possible answers to the following questions.
Each question has only ONE correct answer. Write only the letter (A–D) next to the question number (8.1 – 8.2).
- Power is defined as the rate…..
- of change in velocity.
- at which work is done.
- of change of momentum.
- of change of displacement. (2)
- Which ONE of the following physical quantities is equal to the product of force and average velocity?
- Work
- Average power
- Energy
- Average acceleration (2)
[4]
| Solutions 1. B (2) 2. B (2) [4] |
Activity 9: Power
A car of mass 500 kg accelerates from 10 m·s–1 to 30 m·s–1 in 20 s.
Calculate the power of the car. [5]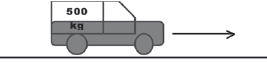
HINT:
- First calculate the work done by applying the work-energy theorem.
- Calculate the power (P).
| Solution Wnet = Δ Ek = ( ½ mvf2 – ½ mvi2) Wnet = (0,5)(500)(302) – (0,5)(500)(102) Wnet = 200 000 J P = W = 200 000 ÷ 20 Δt P = 10 000 W [5] |
Activity 10: Power
A pump is needed to lift water through a distance of 25 m from a borehole at a steady rate of 180 kg/min. What is the minimum power motor that could operate the pump if the velocity at the intake is 4 m·s–1 but at the outlet the water is moving with a speed of 9 m·s–1.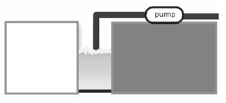
[8]
HINT: In 1 second, the mass of water lifted up is 180kg/60s = 3kg
| Solution Wnc = ΔEk + ΔEp Wnc = ( ½ mvf 2– ½ mvi2) + (mghf – mghi) Wnc = (0,5)(3)(92) – (0,5)(3)(42) + (3)(9,8)(25) – 0 Wnc = 121,5 – 24 + 735 – 0 Wnc = 832,5 J But P = W = 832,5/1 = 832,5 W Δt [8] |
Activity 11: Power
A 0,5 horsepower electric pump is used to bring water out of a borehole that is 80 m deep. 1 horsepower = 745,7 W. Calculate the mass of water that is let out of the borehole in one minute. [5]
| Solution P = 0,5 × 745,7 = 372,85 W P = W Δt 372,85 = W / 60 W = 22 371 J W = FΔy·cosθ F = mg W = mg Δy·cos 0° 22 371 = m × (9,8)(80)cos 0° 22 371 = 784 × m ∴ m = 28,53 kg [5] |
Activity 12: Power
A motor car of mass 1 400 kg moves with a constant speed up a slope that makes an angle of 10° with the horizontal. The motor car experiences a frictional force of 700 N as it moves up the slope.
- Draw a free body diagram to indicate the forces acting on the car. (7)
- Calculate the applied force necessary to move the motor car up the slope at a constant speed. (5)
- If the motor car moves at 80 km·h–1, calculate the power delivered by the motor car’s engine. (3)
[15]
Solutions
|
 (3)
(3) (2)
(2)