Activity 1

1. A sound source approaches a stationary (not moving) observer at constant velocity. Which ONE of the following describes how the observed frequency and wavelength differ from that of the sound source?

   Observed Wavelength	Observed Frequency
   A. Greater than	Greater than
   B. Less than	Less than
   C. Greater than	Less than
   D. Less than	Greater than

   1. Greater than
   2. Less than
   3. Greater than Less than
   4. Less than Greater than (2)
2. Which one of the following is the main principle applied when using the rate of blood flow or the heartbeat of a foetus in the womb?
   
   1. Doppler Effect.
   2. Photoelectric effect
   3. Huygens principle
   4. Diffraction (2)
3. An ambulance approaches an accident scene at constant velocity.
   The siren of the ambulance emits sound waves at a frequency of 980 Hz. A detector at the scene measures the frequency of the emitted sound waves as 1 050 Hz.
   
   1. Calculate the speed at which the ambulance approaches the accident scene. Use the speed of sound in air as 340 m·s^–1 (6)
   2. Explain why the measured frequency is higher than the frequency of the source. (2)
   3. The principle of the Doppler Effect is applied in the Doppler flow meter. State ONE positive impact of the use of the Doppler flow meter on humans. (2)
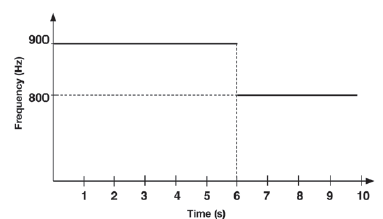
4. The siren of a stationary (not moving) ambulance emits sound waves at a frequency of 850 Hz.
   An observer (person witnessing this) who is travelling in a car at a constant speed in a straight line, begins measuring the frequency of the sound waves emitted by the siren when he is at a distance x from the ambulance. The observer continues measuring the frequency as he approaches, passes, and moves away from the ambulance. The results obtained are shown in the graph below.
   
   
   1. The observed frequency suddenly changes at t = 6s. Give a reason for this sudden change in frequency. (1)
   2. Calculate
      b(1) The speed of the car (Take the speed of sound in air as 340 m·s–1) (5)
      b(2) Distance x between the car and the ambulance when the observer BEGINS measuring the frequency. (3)
      [23]

Activity 2
An ambulance moving at 40 m·s^–1 approaches a traffic light where a blind man and his dog wait to cross a road. The siren of the ambulance (source) emits sound waves at a frequency of 350 Hz (fs). The pitch of the sound that the man hears increases as the ambulance moves towards him and decreases as the ambulance passes him and moves away.

1. If the speed of sound in air is 340 m·s^–1, determine the frequency (fL) of the sound waves that the man hears while the ambulance approaches him. (3)
2. Explain how this effect can help a blind person waiting to cross the road. (2)
   [5]