ELCTROSTATICS - PHYSICAL SCIENCES PAPER 1 STUDY GUIDES AND NOTES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- Definitions: Electrical charge and electric force
- The Law of Conservation of Charge
- Coulomb’s Law
- Electric fields around charged objects
- Electric field strength
Summary
- Electrostatics is the study of static (rest or stationary) positive or negative charges. Think for example of how you can get little shocks from scuffing your feet on a carpet when wearing rubber-soled shoes. This kind of electricity is not flowing, unlike, for example, the electricity in a plug point.
- Define electrostatics, electric field and electric field strength.
- Give evidence for the existence of two kinds of electric charge (like charges repel, unlike charges attract).
- Describe and demonstrate a method for determining whether an unknown charge is positive or negative.
- Name the unit of charge, and discuss its size with respect to common electrostatic situations and in terms of the number of unit charges it represents.
- Describe what it means to say that charge is conserved.
- Coulomb’s Law
- Drawing of electric field lines.
- Application of Coulomb’s Law and electric field strength (by calculations).
6.1 Definitions: Electrical Charge and Electric Force
Electrical Charge
- At the atomic level, charge is associated with protons and electrons. They have the same magnitude of charge, but their charge is opposite in sign. Protons have Positive charge and Electrons have Negative charge. The symbol for a proton is p+ and the symbol for an electron is e–.
- Charge is measured in Coulombs, abbreviated C. It takes 6,25 × 1018 charges to make 1C of charge, i.e. 6 250 000 000 000 000 000 charged particles. 6,25 × 1018 electrons will make –1C of charge. A coulomb is defined technically as one ampere-second (1 As), in other words, the amount of charge carried by one ampere in one second.
- Coulomb’s Law is a measure of how strong the force is between two charged orbjects. Its formula is:
F =kQ 1Q 2
r2 - Electrical charges will exert forces on each other. Two positive charges will repel each other and two negative charges will repel each other. (Like charges, or charges of the same sign, repel each other.) A positive and a negative charge will attract each other. (Unlike charges attract each other.)
- Electrostatic charge is a strong force.
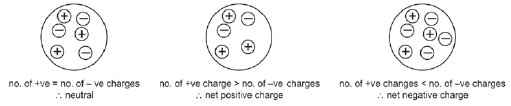
- • As a result most objects usually have about the same amount of positive and negative charge. If they have exactly the same amount of positive and negative charge the net charge is zero and we say they are neutral.
- For convenience, we can abbreviate “positive” and “negative” as +ve and -ve respectively.

Electric Force
- The force is proportional to the product of the charges and inversely proportional to the square of the distance between them. (If we double one charge the force doubles. If both charges are doubled then the force increases by four. If the distance between the charges is increased, the force decreases, and vice versa.) This is similar to Newton's Law of Gravitation, which has the same formula structure.
- Electrical forces can do work and there is a potential energy associated with this force.
6.2 The Law of Conservation of Charge
- When two charged spheres are brought into contact with each
other, electrons flow from the sphere with more electrons to the
sphere with fewer electrons. - The symbol for charge is Q. Do not confuse this with current, Ι.
Q is measured in coulombs and Ι is measured in amperes. - If sphere B has more electrons than sphere A:

Static, rest or stationary have similar meanings in science
REMEMBER: when charges are brought into contact they must be added and then divided by TWO to get an average.
Charge cannot be destroyed or created, but can only be transferred from one object to another.
Worked example 1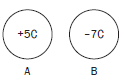
Two spheres A and B carry charges of +5 C and −7 C respectively. They are brought into contact and are then separated.
- What is the nature of the force between the charges before they are allowed to touch? Explain.
- In which direction are electrons transferred during the contact? Explain.
- Calculate the total charge in the system.
- Calculate the charge on each sphere when they are separated.
- Calculate the change in the charge on A and on B.
- Calculate the number of electrons transferred from one sphere to the other.
Solutions
1. Attraction. Opposite charges (+ and −) attract.
2. From sphere B to sphere A. Electrons are transferred from the sphere with the most electrons (B in this case) to the sphere with the least electrons (A).
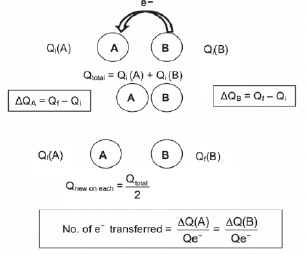
3. Qtotal = Qi (A) + Qi (B) = +5 + (−7) = −2 C
4. Qnew on each = Qtotal = -2 = −1 C = Qf
2 2
5. ΔQA = Qf – Qi = −1 – (+5) = −6 C ∴ 6 C charge was transferred from B to A
ΔQB = Qf – Qi = −1 – (−7) = +6 C ∴ 6 C charge was transferred from B to A
6. No. of e– transferred ΔQ(A)= No. of e– transferred = ΔQ(B)
Qe- Qe-
= 6 or 6
1.6 × 10-10 1.6 × 10-19
= 3,75 × 1019 electrons
6.3 Coulomb’s Law
Coloumb’s Law is the electrostatic force of attraction or repulsion between two charged objects is directly proportional to the product of the charges and inversely proportional to the square of the distance between their centres.
For any two charges, where F is electrostatic force (N), Q is charge (C), r is the distance between the centres of the objects (m), and k is Coulomb’s constant (9 x 109 Nm2C–2)
F ∝ Q1 · Q2 and F ∝ 1
r2
∴ F = kQ 1Q 2
r2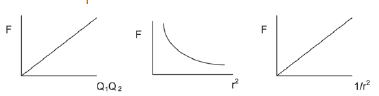
6.3.1 Using Coulomb’s Law
We apply Coulomb’s Law to determine how the electrostatic force between two charged objects (or point charges) changes when the charge on one or both of the objects changes and when the distance between their centres changes.
We can also use Coulomb’s Law to calculate the electrostatic force between two charges, the distance between them, or the magnitudes (sizes) of the charges.
Worked example 2
The original force between two charges is F. If both charges are doubled and the distance is a third of the original distance, what is the magnitude of the new force relative to the original force?
Solution
Foriginal = kQ 1Q 2
r2
Fnew = k(2Q1)(2Q2)
(1/3r)2
Fnew = 4kQ 1Q 2 = 36kQ 1Q 2 = 36Foriginal
1/3r2 r2
Remember to square the distance.
Worked example 3
Two small identical metal spheres carry equal but opposite charges. If their centres are 30mm apart, and the electrostatic force between them is 2.56 × 10–3N. Calculate:
- The magnitude (size) of the charge on each sphere
- The number of electrons that would flow from the negatively charged sphere to the positively charged sphere if they were brought into contact.
Solutions
- F = kQ 1Q 2
r2
2,56 × 10–3 × 0,0009 (9 × 10–4) = 9 × 109 × Q × Q
2,304 × 10–6 / ( 9 × 109) = Q2
Q2 = √2,56 × 10–16 ; Q = 1,6 × 10–8C - number of electrons = total charge
charge on one electron
= (1,6 × 10–8) / (1,6 × 10–19)
= 1 × 1011 electrons
‘Charges are unknown’ this means I need to calculate them.
I must remember just not forget to convert mm to m.
Activity 1
Two small identical metal spheres, A and B carrying charge of –4 × 10–12C and –3 × 10–12C respectively, are mounted on insulated stands as shown.
The distance between the centres of the spheres is 5 cm.
- Calculate the magnitude and direction of the force that A exerts on B. (6)
Sphere A is moved and makes contact with sphere B. It is then moved back to its original position. - Calculate the new charge on each of the spheres. (3)
- How does the magnitude of the force that the sphere A exerts on sphere B change? Answer by writing ONLY increases, decreases or remains the same. (2)
[11]
Solutions
|
Start by converting the distance 5cm to m. Look at the conversion table.
6.4 Electric Fields around Charged Objects
- Electric fields are represented by field lines as illustrated in the diagrams below.
- Electric field is a vector quantity.
- An electric field line indicates the direction in which a positive test charge would move if placed at a point in the electric field.
6.4.1 Properties of electric field lines
Electric field lines:
- start and end perpendicular to the surface of a charged object
- never cross each other
- are closer where the electric field is stronger
- are directed from positive to negative
6.4.2 Representing electric fields
You must be able to draw simple diagrams to show the electric fields around charged objects.
| a) Around a positive point charge 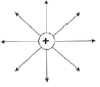 | b) Around a negative point charge 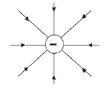 |
| c) Between two like point charges of equal magnitude (both positive or both negative) 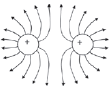 If the point charges are negative, the arrows point inwards, towards the point charges. | d) Between two like point charges that are not equal in magnitude 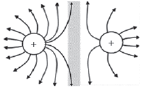 The field lines are closer together when the electric field is stronger (around the greater charge). |
| e) Between two unlike (opposite) point charges (one positive and the other negative) 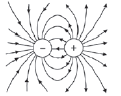 | f) Between two oppositely charged(one positive and one negative) parallel plates 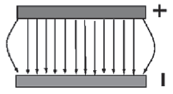 This electric field is uniform – it is equally strong everywhere between the two plates, so the electric field lines are equally spaced and parallel. |
Remember: The arrows representing electric field lines ALWAYS point away from a positive charge and towards a negative charge.
Definition: An electric field is a region or space in which an electric charge experiences an electric force.
6.5 Electric Field Strength
Formula
The electric field strength at a point is the electric force per unit positive charge experienced at a point in an electric field.
For any charge:
E = F and ∴ E = kQ
Q r2
Worked example 4
Two point charges, Q1 and Q2, at a distance of 3 m apart, are shown below. The charge on Q1 is –14 μC and the charge on Q2 is +20 μC.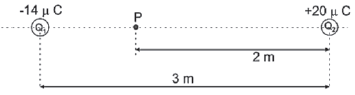
Remember:
First convert μC to C: –14 μC = –14 × 10–6 C and 20 μC = 20 × 10–6 C
- Define the electric field strength at a point.
- Calculate the net (resultant) electric field at point P situated 2 m from Q2.
Solutions
- Electric field strength at a point is the electric force per unit positive charge experienced at the point.
- Electric field at P due to Q1:
E = kQ = (9 × 109)(14 × 10–6)
r2 12
= 1,26 × 105 N·C–1 to the left
Electric field at P due to Q2:
E = kQ = (9 × 109)(20 × 10–6)
r2 12
= 4,5 × 104 N·C–1 to the left
Let ← E+
Enet = EQ1 + EQ2
= (+1,26 × 105) + (+4,5 × 104 N·C–1)
= +1,71 × 105 N·C–1
∴ 1,71 × 105 N·C–1 to the left
The values substituted are positive (+), because left is chosen as positive and both the electric fields are directed to the left.
Step by step
Step 1. ALWAYS calculate the electric field strength at the given point (P in this case) due to each of the point charges first. The negative sign for a negative charge is NOT used in this equation.
Step 2. Then choose an electric field direction as positive and state this clearly.
Step 3. Then find the resultant (or net) electric field strength by adding the two field strength values. Lastly, remember the signs for the directions!
Activity 2
Multiple Choice Questions:
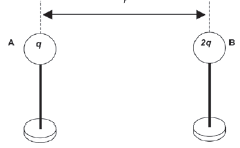
- The sketch below shows two small metal spheres, A and B, on insulated stands carrying charges of magnitude q and 2q respectively.
The distance between the centres of the two spheres is r.
Sphere A exerts a force of magnitude F on sphere B. What is the magnitude of the force that sphere B exerts on sphere A?- ½ F
- F
- 2F
- 4 (2)
- Two identical small metal spheres on insulated stands carry equal charges and are a distance d apart. Each sphere experiences an electrostatic force of magnitude F.
The spheres are now placed a distance ½ d apart.
The magnitude of the electrostatic force each spheres now experience is..- ½ F
- F½
- 2½ F
- 4F (2)
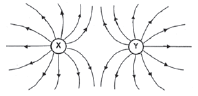
- Three identical point charges, q1, q2 and q3, are placed in a straight line, as shown below. Point charge q2 is placed midway between point charges q1 and q3. X and Y are two points on the straight line as shown.

Which ONE of the following best describes how the electric field E at a point X compares to that at point Y?
| DIRECTION OF E | MAGNITUDE OF E |
| A. Same | EX > EY |
| B. Same | EX < EY |
| C. Opposite | EX > EY |
| D. Opposite | EX < EY |
[6]
| Solutions 1. B (2) 2. D (2) 3. D (2) [6] |
Activity 3
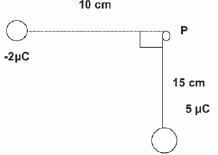
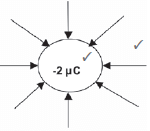
A negative charge of 2 μC is positioned 10 cm from point P, as shown below.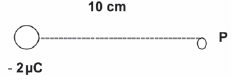
- Define the electric field at point P in words. (2)
- Draw the electric field lines associated with this charge. (2)
- A positive charge of 5 μC is now positioned 15 cm from point P, as showed in the diagram below.
Calculate the magnitude of the electric field at point P due to both charges. (12)
[16]
Solutions
| ||||||
Activity 4
The centres of two small, charged conducting spheres, X and Y, on insulated stands, are separated by a distance of 60 mm. Sphere X initially carries a charge of +12 × 10–9 C.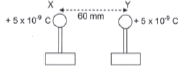
X and Y are brought into contact with each other and are separated again.
After separation, each sphere carries EQUAL charges of +5 × 10–9 C.
- Draw a neat diagram of the resultant electric field pattern that surrounds X and Y. (4)
- Calculate the number of electrons that must be added to Y to make it neutral. (3)
- Calculate the magnitude of the force which X exerts on Y once they are back in their original positions (after separation). (4)
- Calculate the original charge on sphere Y. (4)
[15]
Solutions
|