GRADE 12 MATHEMATICAL LITERACY PAPER 1 QUESTIONS - NSC PAST PAPERS AND MEMOS JUNE 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICAL LITERACY P1
GRADE 12
JUNE 2016
NATIONAL SENIOR CERTIFICATE
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions.
- Answer ALL the questions.
- Use the ANNEXURES to answer the following questions:
ANNEXURE A for QUESTION 3.1
ANNEXURE B for QUESTION 3.2 (Table 1 and 2).
ANNEXURE C for QUESTION 4.2 (Table 3)
ANSWER SHEET 1 for QUESTION 5.1.2
Write your GRADE and your NAMES in the spaces provided on the
ANSWER SHEET and hand it in with your ANSWER BOOK. - Number the questions correctly according to the numbering system used in this question paper.
- Diagrams are NOT necessarily drawn to scale.
- Round off ALL the final answers according to the context used, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Start EACH question on a NEW page.
- Show ALL calculations clearly.
- Write neatly and legibly.
QUESTION 1
Mambo SSS, is a small private school in the Lady Frere area of the Eastern Cape. In 2015 it had a total of 167 registered learners that were as follows:
| GRADE | GIRLS | BOYS | TOTAL |
| 8 | 21 | 18 | 39 |
| 9 | 15 | 20 | 35 |
| 10 | 13 | 7 | 20 |
| 11 | 19 | A | B |
| 12 | 25 | 17 | 42 |
| TOTAL | 93 | 74 | 167 |
| Fees are payable according to the grade. A learner in Grade 8 or 9 paid R300 per month for the 11 months and in Grade 10–12 each learner paid R450 per month for 11 months (January–November). The School Governing Body (SGB) exempted a total of 8 learners in Grade 12 from paying school fees for the 2015 year. The exempted learners were in the ratio boys : girls = 1 : 3. At the April meeting of the SGB it resolved to increase the fees for Grade 8 and 9 by 5% and reduce the Grade 10–12 fees by 2,5%. The adjustments were effective from May 2015. | |||
1.1 Determine the total school fees collected in January 2015 if all parents paid. (4)
1.2 Calculate the total school fees of the girls who were exempted would have paid in January 2015. (2)
1.3 Determine the monthly school fees payable by each learner in the school after the SGB meeting in 2015. (4)
1.4 Calculate the total school fees that were collected in 2015 if no parent defaulted on payment. (4)
1.5 An amount of R150 000 from the collected school fees in 2015 was invested in a fixed account with FNB. The investment attracts a simple interest rate of 9,5% per annum for the period January to December 2016.
Work out the interest the school will earn from the investment. (2)
1.6 Calculate the value of A, the number of boys in Grade 11. (2)
1.7 Determine the probability of randomly selecting a Grade 11 learner from the school. Give your answer as a decimal. (2)
[20]
QUESTION 2
Thabo bakes round biscuits known as-Rb for sale. He packs the biscuits in a cylindrical container made up of cardboard material. The diagram below shows the container and its dimensions.
The diagram not drawn to scale.
| ?????ℎ ?? ?ℎ? ???????? (?) = 270 ?? ???????? (?) = 90 ?? |
The following formulae may be used in answering the questions that follow.
Area of the circle = ??2 ,where ? = 3,142
Total surface area = 2??2 + 2 ?? ?
Volume of the cylinder = ??2?
2.1.1 Calculate the total surface area of the cardboard package required to make one cylindrical container. (4)
2.1.2 The rectangular cardboard used to make the cylindrical containers, is bought at a price of R5 a piece measuring 120 cm by 60 cm.
Work out the area of the rectangular cardboard in ??2. (3)
2.1.3 Use your answers in QUESTIONS 2.1.1 and 2.1.2 to determine the number of cylindrical containers that can be made from one piece of the cardboard. (3)
2.2
| Thabo discovered that his tap was faulty and has been leaking water drops at a rate of one drop every 2 seconds. The water that was wasted, was a litre every 4 hours. Note: 1 k? = 1 000 ?; 1 ? =1 000 ??; 1 ? = 1 000 000 microlitres. |
2.2.1 Calculate the number of drops of water that filled a litre container.
Use the formula:
?????? ?? ????? = ??????? ?? ? ???? × ??.?? ?????
???? ?? ??? ?????
(3)
2.2.2 Calculate the volume of one drop of water in microlitres. (2)
2.2.3 Work out the amount of water wasted from 01/01/2016 to 31/05/2016. Give your answer in litres. (3)
[18]
QUESTION 3
3.1 The floor plan of a house on sale in Johannesburg is shown on ANNEXURE A. Study the floor plan and the information given to answer the questions that follow.
1′ = 30,48 ??
1′′ = 2,54 ??
3.1.1 Determine the total number of doors that can be seen on the floor plan. (2)
3.1.2 Give the general direction of the bedroom measuring 11' × 10'4'' from the porch. (2)
3.1.3 Calculate the dimensions of the bedroom measuring 11'× 10'8'' in metres. (4)
3.1.4 The floor plan was drawn using a scale of 1,5 cm on the floor plan to represent 3,375 m on the actual building. Determine the scale used in the form of 1 : … (3)
3.2 Use Tables 1 and 2 in ANNEXURE B to answer the following questions.
3.2.1 Mr Dan departed on Friday from East London to meet an agent in Johannesburg on Saturday at 11:15 am as per arrangement.
Write down the departure time from East London and arrival time in Johannesburg. (2)
3.2.2 Identify the station where Shosholoza-Meyl train stopped for the longest duration. (2)
3.2.3 The total time spent at the stations during the journey was 3 hours and 33 minutes. Calculate the average speed of the journey (East London– Johannesburg). Give your answer in Km/h.
You may use the following formula:
??????? ????? = ????????
????
???? = ?????????? ??????? ??????? ???? ??? ????????? ???? − ????? ???? ????? ?? ??? ???????? (4)
[19]
QUESTION 4
4.1 The diagram below shows the Weight-for-age growth chart for boys from birth to 2 years. Use the growth chart to answer the questions that follow.
GROWTH CHART FOR BOYS
4.1.1 Explain what it means if the baby’s weight-for-age relationship is on the 85th percentile curve. (2)
4.1.2 Determine the weight of an 11-month-old baby whose weight-forage relationship is on the 50th percentile curve. (2)
4.1.3 Consider a 18-month-old baby with a weight of 11 kg:
- On which percentile curve is this baby’s weight-for-age relationship? (2)
- Calculate the body mass index (BMI) for this baby if he is 80 centimetres tall.
Use the formula: BMI = Weight (in kilogram)
(Height in metres )2
(3)
4.2
| The 2015 National Senior Certificate (NSC) results that was released showed a decrease in national achievement from 75,8% in 2014 to 70,7% in 2015. However there was an increase of 117 798 learners achieving a NSC qualification in 2015 compared to 2014. TABLE 3 on ANNEXURE C shows the 2015 NSC ACHIEVEMENT BY TYPE OF QUALIFICATION. |
Use the information on ANNEXURE C to answer the following questions.
4.2.1 Calculate the total national number of learners that achieved a NSC qualification in the 2014 examinations. (2)
4.2.2 Determine the total national number of learners that did not achieve a NSC qualification in the 2015 NSC examinations. (2)
4.2.3 Calculate the value of A, the percentage of learners who qualified for admission to study for a Bachelors’ degree in 2016. (2)
4.2.4 Show how the 23,0% for Diploma achievement for the Eastern Cape was calculated. (3)
4.2.5 Arrange the percentages (%) of the overall achievement of the provinces in ascending order and identify the province occupying the median position. (3)
4.2.6 Determine the probability of a learner from the Gauteng Province achieving a NSC qualification in 2015. Give your answer in a decimal form to 3 decimal places. (2)
[23]
QUESTION 5
5.1 Jane, a learner from Mambo SSS sells fat cakes her mother bakes at home.
| She calculated the cost of the ingredients that is needed to make one fat cake as follows: | |
| INGREDIENT | COST |
| Bread flour | 0,70 |
| Sugar | 0,75 |
| Salt | 0,05 |
| Instant yeast | 0,20 |
| Water | 0,05 |
| Oil for deep frying | 0,50 |
The mother is charging her R0,25 for labour for every fat cake sold. She sells each fat cake at R3,00 as a zero rated item. Jane hires a space at school for R50 per month from where she sells her fat cakes.
Use the above information to answer the following questions:
5.1.1 Calculate the variable cost for making one fat cake. (2)
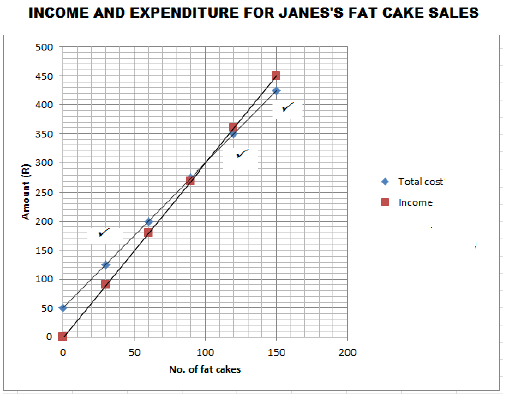
5.1.2 The table below shows information for the income and expenses for fat cakes
TABLE 4: Income and expenditure for Jane’s fat cakes
| No. of fat cakes (n) | 0 | 30 | 60 | 90 | 120 | 150 |
| Total cost (R) | 50 | 125 | 200 | 275 | 350 | 425 |
| Income(R) | 0 | 90 | 180 | 270 | 360 | 450 |
Use the information from the above TABLE to draw a straight line graph that represents the cost in ANSWER SHEET 1. (3)
5.1.3 Using the graph or otherwise determine the number of fat cakes she must sell to breakeven. (2)
5.2 Jane was chosen to visit Japan on a student entrepreneurship exchange programme during July holiday of 2016. She read from internet that the smallest form of the Japanese currency is a 1 yen coin. She exchanged R925 for Japanese yen.
Yen( ¥) 1 = Rand (R) 0,13
Use the given exchange rate to determine how many yen (¥) she will receive from changing her Rand value (2)
5.3
| Mr Tawi is tired of renting and would like to buy a house in East London valued at R880 000 this year. The bank he approached offered him a home loan of R748 000. He was provided with a factor table as shown below to use in calculating his monthly repayment. |
HOMELOAN REPAYMENT FACTOR TABLE
| Term | Interest rates | ||||||
| 7% | 8% | 9% | 10% | 11% | 12% | 13% | |
| 20 years | 7,75 | 8,36 | 9,00 | 9,65 | 10,32 | 11,01 | 11,72 |
| 25 years | 7,07 | 7,72 | 8,39 | 9,09 | 9,80 | 10,53 | 11,28 |
| 30 years | 6,65 | 7,34 | 8,05 | 8,78 | 9,52 | 10,29 | 11,05 |
| He decided to repay the loan over a 25 year period at an interest rate of 12% p.a. compounded monthly. Use the information and the above table to answer the questions that follow. |
5.3.1 Determine his monthly repayment.
You may use the following formula:
Monthly repayment = ?????? ???????× ?????? (2)
? ???
5.3.2 Calculate what the price for this house was in 2015 if the current inflation rate is 5,7% (3)
5.4 The results of the controlled test in March 2016 for the Grade 12 Mathematical Literacy learners at Mambo SSS are listed below:
| 38 | 54 | 20 | 61 | 60 | 21 | 31 | 54 | 65 | 76 |
| 48 | 60 | 5 | 22 | 63 | 17 | 15 | 66 | 54 | 59 |
| 73 | 31 | 98 | 26 | 42 | 67 | 8 | 5 | 46 | 54 |
Use the above table of results to answer the questions that follow.
5.4.1 Identify the mark that represents the mode of the class performance. (2)
5.4.2 Determine the range of the performance of this class. (2)
5.4.3 The Curriculum and Assessment Policy Statement (CAPS) has a seven point scale to rate a learner’s performance as follows:
| Rating Code | Description of competence | Percentage |
| 7 | Outstanding achievement | 80%–100% |
| 6 | Meritorious achievement | 70%–79% |
| 5 | Substantial achievement | 60%–69% |
| 4 | Adequate achievement | 50%–59% |
| 3 | Moderate achievement | 40%–49% |
| 2 | Elementary achievement | 30%–39% |
| 1 | Not achieved | 0–29% |
Determine the probability that a learner randomly chosen has obtained substantial achievement. (2)
[20]
TOTAL: 100
ANNEXURE A: PLAN OF A HOUSE
QUESTION 3.1
ANNEXURE B: QUESTION 3.2
TABLE 1: Shosholoza-Meyl Train schedule
| Johannesburg – East London (Wednesday, Friday and Sunday Service) | ||||
| Station | Class available | Day | Arr. | Dep. |
| Johannesburg | Sleeper/Sitter | Day 1 | 17:30 | |
| Vereeniging | Sleeper/Sitter | Day 1 | 19:00 | 19:20 |
| Kroonstad | Sleeper/Sitter | Day 1 | 21:42 | 21:50 |
| Bloemfontein | Sleeper/Sitter | Day 2 | 00:32 | 00:55 |
| Burgersdorp | Sleeper/Sitter | Day 2 | 06:17 | 06:34 |
| Queenstown | Sleeper/Sitter | Day 2 | 08:58 | 09:12 |
| East London | Sleeper/Sitter | Day 2 | 13:25 | |
| East London – Johannesburg (Wednesday, Friday and Sunday Service) | ||||
| Station | Class available | Day | Arr. | Dep. |
| Queenstown | Sleeper/Sitter | Day 1 | 09:00 | |
| East London | Sleeper/Sitter | Day 1 | 13:05 | 13:26 |
| Burgersdorp | Sleeper/Sitter | Day 1 | 16:00 | 18:28 |
| Bloemfontein | Sleeper/Sitter | Day 1 | 21:36 | 21:56 |
| Kroonstad | Sleeper/Sitter | Day 2 | 00:51 | 01:10 |
| Vereeniging | Sleeper/Sitter | Day 2 | 03:20 | 03:25 |
| Johannesburg | Sleeper/Sitter | Day 2 | 05:00 | |
TABLE 2: Distances between the major towns:
| The distances given below are for the shortest possible routes | |
| Town A to Town B | Distances (km) |
| Cape Town–Johannesburg | 1 405 |
| Cape Town–Durban | 1660 |
| East London–Cape Town | 1042 |
| Cape Town–Port Elizabeth | 756 |
| Cape Town–Bloemfontein | 998 |
| Cape Town–Upington | 821 |
| Johannesburg–Durban | 598 |
| East London– Johannesburg | 992 |
| Johannesburg–Polokwane | 331 |
NAME:
ANSWER SHEET 1
QUESTION 5.1.2
INCOME AND EXPENDITURE FOR JANE’S FAT CAKE SALES
ANNEXURE C
QUESTION 4.2
TABLE 3: 2015 NSC ACHIEVEMENT BY TYPE OF QUALIFICATION
| PROVINCE | TOTAL WROTE | Bachelor | Diploma | Higher Certificate | Some information omitted | |||||
| Achieved | % Achieved | Achieved | % Achieved | Achieved | % Achieved | TOTAL Achieved | % Achieved | |||
| EASTERN CAPE | 87090 | 15291 | 17,6 | 20055 | 23,0 | 14119 | 16,2 | 49475 | 56,8 | |
| FREE STATE | 31161 | 9277 | 29,08 | 11026 | 35,4 | 5102 | 16,4 | 25416 | 81,6 | |
| GAUTENG | 108442 | 38760 | 35,7 | 37375 | 34,5 | 15191 | 14,0 | 91327 | 84,2 | |
| KWAZULU NATAL | 162685 | 34751 | 21,4 | 39799 | 24,5 | 24180 | 14,9 | 98761 | 60,7 | |
| LIMPOMPO | 101575 | 20992 | 20,7 | 25434 | 25,0 | 29513 | 20,2 | 66946 | 65,9 | |
| MPUMALANGA | 54980 | 13497 | 24,5 | 18675 | 34,0 | 11046 | 20,1 | 43229 | 78,6 | |
| NORTH WEST | 33286 | 8865 | 26,6 | 1154 | 34,7 | 6699 | 20,1 | 27118 | 81,5 | |
| NORTHERN CAPE | 11623 | 2451 | 21,1 | 3306 | 28,4 | 2306 | 19,8 | 8064 | 69,4 | |
| WESTERN CAPE | 53721 | 22379 | 41,7 | 16496 | 30,7 | 6614 | 12,3 | 45489 | 84,7 | |
| NATIONAL | 644536 | A | 183720 | 28,5 | 105770 | 16,4 | 455825 | 70,7 | ||