ElimuZA Access to Education
GRADE 12 MATHEMATICAL LITERACY PAPER 1 MEMORANDUM - NSC PST PAPERS AND MEMOS JUNE 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICAL LITERACY P1
GRADE 12
JUNE 2016
MEMORANDUM
NATIONAL SENIOR CERTIFICATE
| Symbol | Explanation |
| M | Method |
| A | Accuracy |
| CA | Consistent accuracy |
| RT/RG/RM | Reading from a table/Reading from a graph/Read from map |
| SF | Substitution in a formula |
| P | Penalty, e.g. for no units, incorrect rounding off etc. |
| S | Simplification |
| R | Rounding/Reason |
| QUESTION 1 (Answer only FULL marks) | |||
| Quest | Solution | Explanation | Marks |
| 1.1 | Total in Grades 8–9 = (39 + 35) = 74 Jan. fees = 74 × 300 = R22 200 ✓ MA Total paying learners in Grades 10–12 = 167 – (74 + 8) = 85 ✓ Jan Fees = 85 × 450 = R38 250 ✓ MA Total school fees for Jan = 22 200 + 38 250 = R60 450 ✓ CA | 1MA amount R22 200 1 S 1MA amount R38 250 1CA amount | (4) |
| 1.2 | Boys: Girls = 1 : 3 Girls = 3/4 ×8 = 6✓M Girls would have paid = 6 × 450 =?2700 ✓CA | 1M for 6 1CA amount | (2) |
| 1.3 | Gr 8 and 9 will pay = 1,05 × 300 ✓ MA = R315 ✓ ?A Grades 10 and12 will pay = 0.975 ×450 ✓ M =R438,75 ?✓ OR Increase = 5100×300=?15 ✓ M New fees = 300 + 15 = R315 ✓ A Decrease = 2.5/100 ×450 = R11.25✓ M New fees = 450 – 11,25 = R438,75 ?✓ | 1MA multiply by 1,05 1CA 1M multiplying by 0,975 1A amount 1MA 5% OF 300 1A amount 1M 2,5% of 450 1A | (4) |
| 1.4 | Fees for Jan–April = 60 450×4 = R241 800 ✓ CA Fees for May-Nov 7 × 315 ×74 + 7×438,75× 85 ✓ ?? ✓?? 163 170 + 261 056,25 = 424 226,25 Total for the year = 424 226,25 + 241 800 R666 026,25✓ CA | 1CA from 1.1 Multiplying value from 1.1 by 4 months 1CA from 1.3 for 7 × 315 ×74 1CA For 7 × 438,75 × 85 1CA amount | (4) |
| 1.5 | Amount after the year Jan–Dec 2016: = 150 000 ×1.095 ×1=?164 250 ✓A Interest = 164 250 -150 000 = R14250 √A OR ✓?? Interest for one year = 150 000 ×(9.5/100)×1 = R14 250 ✓A | 1A amount end of 2016 1A amount 1MA Multiplication with correct values 1A amount | (2) |
| 1.6 | Number in Gr 11 = 167 – (42 + 20 + 35 + 39) = 31 ✓M (Value of B) No. of Boys = 31 – 19 = 12 √A | 1M 1A | (2) |
| 1.7 | P(learner in gr 11)= 32/167 ✓MA =0,19✓?A | CA from 1.6 1MA 1 CA | (2) |
[20]
| QUESTION 2 (Answer only FULL marks) | ||||
| 2.1 | 2.1.1 | Cardboard package to make the cylinder Surface area SF = 2 × 3,142 ×(90/2)2✓+ 2 × 3,142 × 270 × 90 = 12 725,10 +76 350,60 ✓ S = 89 075,7 ✓??2 ✓CA | 1SF 1S 1CA 1 A unit | (4) |
| 2.1.2 | Area of the cardboard = 120 × 60✓?X100 ✓ C = 720 000 ??2✓A OR Area of Cardboard = 1 200 × 600 ✓✓ M & C = 720 000 ??2 ✓A | 1M 1C to ??2 1A in ??2 | (3) | |
| 2.1.3 | No. of the cylindrical containers | 1M Division 1CA from 2.1.1 and 2.1.2 1CA whole number rounding down | (3) | |
| 2.2 | 2.2.1 | No. of drops = (60×60×4)/2✓ ??=7200 ????? ✓A | 1MA Substitution 1A | (2) |
| 2.2.2 | 7200 drops = 1000 000 ???????????=1? One drop = 1000000✓/7200✓? =138,89 ???????????✓?? | 2M Division 1CA | (3) | |
| 2.2.3 | Water wasted = 152 days✓ ?×244 ✓ M = 912 l✓CA | 2M Multiplication Values152 and 6 l 1CA in litres | (3) | |
[18]
| QUESTION 3 (Answer only FULL marks) | ||||
| 3.1 | 3.1.1 | ✓✓? 18 (this number excludes wardrobe doors) Accept 21 doors (this number includes wardrobe doors) 1 mark Accept 26 doors for learners that see a double door as two doors 1 mark) | 2A for 18 doors 1A for 21 1AS for 26 | (2) |
| 3.1.2 | North West ✓✓ A | 2A | (2) | |
| 3.1.3 | 11'×30.48 cm = 335,28 cm ✓ ?? Length = 335.28 = 3.3528 m ✓ C? 10 ' =10×30.48 cm = 304,8 cm 8′′=8×2,54 =20,32 ?? ✓ MA Total length = 20,32+304,8 = 325,12 cm = 3,2512 m ✓ A Dimensions are: 3,3528 m by 3,2512 m | 1MA multiplying by 30,48 1CA 1MA Multiplying by 2,54 cm 1CA | (4) | |
| 3.1.4 | 1,5cm diagram represents 3.375m on the building | 1M for same units 1M dividing 1,5 1A 1M for same units 1M dividing 0,015 1A | (3) | |
| 3.2 | 3.2.1 | East London 09:00 ✓ ? OR 9 in the morning✓ OR 9 am✓ Johannesburg 05:00 ✓ A OR 5 in the morning✓ OR 5 am✓ | 1A 1A | (2) |
| 3.2.2 | Burgersdorp: ✓✓ A | 2A | (2) | |
| 3.2.3 | Average speed = ????? ???????? ????? ???? Total time = (24:00-9: 00 +5:00)-3hrs 33min = 20h – 3h 33min =16h 27min ✓ A ✓ ? ✓ SF = 992?? 16ℎ? 27 = 992?? 16.45 = 60,30 Km/h✓ | 1A value for time 16h 27 min 1A Value for distance – numerator 1SF 1 CA | (4) | |
[19]
| QUESTION 4(Answer only FULL marks) | ||||
| 4.1 | 4.1.1 | This means that 15% of the babies weigh more than the baby and 85% weigh less than the baby. ✓✓ | 2A Explanation | (2) |
| 4.1.2 | 9,4 kg. ✓ RD Accept (9,3–9,5) kg | 2A RD | (2) | |
| 4.1.3 | (a) 50th Percentile ✓✓ RD | 2A RD | (2) | |
| (b) BMI = Weight (in kilogram) (Height in metres )2 ✓ SF = 11 ?? (0,8)2 ✓ SF =17,19 ?? ?2 ✓ CA | 2SF substitution 11 kg and 0,8 m 1CA | (3) | ||
| 4.2 | 4.2.1 | Learners achieved NSC In 2014 = learners achieved in 2015 –117 798 ✓ M = 455 825-117 798 = 338 027 ✓ A | 1M Subtraction 1A | (2) |
| 4.2.2 | Total learners not achieving NSC = 644 536-455 825 ✓ M = 188 711✓ A | 1M subtraction 1A | (2) | |
| 4.2.3 | ✓M % achieved Bachelor = (166 263/644 536)×100 = 25.8%✓ CA | 1M adding Bachelor passes 166 263 1CA | (2) | |
| 4.2.4 | NSC Diploma achievement for EC ✓M = (20055/87090)×100=23,03 ✓CA = 23,0% ✓A 1M dividing 20 055 by the total 87 090 1CA | 1A use of 1decimal.place within the context | (3) | |
| 4.2.5 | Ascending order of the % achievements 56,8%; 60,7%; 65,9%; 69,4%; 78,6%; 81,5%; 81,6%; 84,2%; 84,7%. ✓✓MA Median 78,6% and province: Mpumalanga ✓CA | 2MA correct arrangement If descending order only 1 Mark 1CA Province not % | (3) | |
| 4.2.6 | P( Learner achieved NSC in Gauteng in 2015) = 84,2% ✓M = 0.842✓ A OR (91327/108442) ×100 = 0,84217% ✓ = 0,842 ✓ | 1M Value of 84,2% 1A decimal form to 3 decimal places | (2) | |
[23]
| QUESTION 5 (Answer only FULL marks) | ||||
| 5.1 | 5.1.1 | Variable cost = 0.70 + 0.75 + 0,05 + 0,20 + 0.05 + 0,50 + 0,25 MA = R2,50 ✓A | 1MA adding cost of ingredients and labour 1A amount | (2) |
5.1.2 | 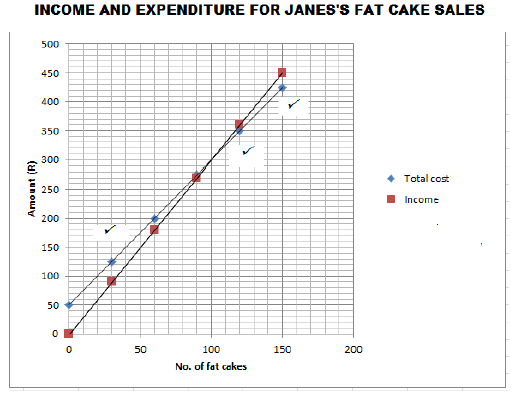 | |||
| Plotting 3 points correctly 1 Mark ×2= 2. Drawing the line ✓A | 2MA Plotting correctly 1CA Straight line Through the points | (3) | ||
| 5.1.3 | 100 fat cakes to be sold to break even (form graph) ✓✓ RD OR 50+ 2,5n = 3n✓✓ 50 = 3n – 2,5n 50 = 0,5n 500 = 5n ∴ n = 100✓A | 2RD From the point of intersection. 1M equating the cost = production 1A for 100 fat cakes | (2) | |
| 5.2 | 1 Yen ¥ = R0,13 ?? = R925 ✓ M ?? = 925/0.13 = 7115.384 ∴amount of Yens (¥) = 7115 ✓✓ | 1M Division of the values 1A amount (7115) smallest coin ¥ 1 | (2) | |
| 5.3 | 5.3.1 | ✓SF Monthly repayment = 748 0001000×10,53=?7 876,44 ✓ | 1SF Substitution 1CA amount | (2) |
| 5.3.2 | Price for the house in 2015 ✓M = 880 000/1,057✓✓=?832 544,94 ✓✓ OR Inflation = (5,7/105,7)×880 000=47 455,06✓A ✓M 2015 Price = 880 000 - 47 455,06 = R832 544,94 ✓A OR 2015 Price + 5,7% of 2015 price = 880 000 2015 Price (1+ 5,7%) = 880 000 ✓ M 2015 Price = 880 000/1,057✓ = R832 544,94 ✓ OR Price in 2015 = ? Price in 2016 = + ?(5.7/100) of ? 880 000 = ? + (5.7/100) ×? 880 00× 100 = 100 ?+ 5,7 ? = 105,7 ? ✓?? ? = (880 00 × 100)/105,7 ✓ = R832 544,94 √A | 1M Division 1A Value 1,057 1CA amount OR 1A for inflation value 1M Subtraction 1CA amount 1MA numerator 1A denominator 1A amount | (3) | |
| 5.4 | 5.4.1 | Mode mark = 54 ✓✓ A | 2A | (2) |
| 5.4.2 | The range 98 – 5 = 93 ✓✓ A | 2A | (2) | |
| 5.4.3 | P(learner obtained Substantial) = 6/30 =1/5 = 0,2 ✓✓ A = 20% | 2A (allow fraction or decimal or %) | (2) | |
[20]
TOTAL: 100
Published in Grade 12 2016 June Exams, Past Papers