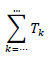MATHEMATICS P1
GRADE 12
JUNE 2016
NATIONAL SENIOR CERTIFICATE

INSTRUCTIONS AND INFORMATION

Read the following instructions carefully before answering the questions.

1. This question paper consists of 10 questions. Answer ALL the questions.
2. Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
3. Answers only will not necessarily be awarded full marks.
4. You may use an approved scientific calculator (non-programmable and non- graphical), unless stated otherwise.
5. If necessary, round off answers to TWO decimal places, unless stated otherwise.
6. Diagrams are NOT necessarily drawn to scale.
7. An information sheet, with formulae, is included at the end of the question paper.
8. Number the answers correctly according to the numbering system used in this question paper.
9. Write neatly and legibly.
   
   

QUESTION 1
1.1 Solve for x, in each of the following:
1.1.1 2?2 − 7? = 0 (3)
1.1.2 4? + 4 + 11 = 0 ; ? ≠ 0 (correct to TWO decimal places) (4)
                 ?
1.1.3 (2? − 1)(? − 3) > 0 (3)
1.1.4 3^? . 3^?+1 = 27^? (4)
1.2 Solve simultaneously for x and y in the following equations:
3 + ? = 2? and 4?² + ?² = 2?? + 7 (6)
1.3 Given: ?(?) = ?³ − 4?² − 2^? + 20 = (? + 2)(?² − 6? + 10)
Prove that ?(?) has only one real root. (3)
[23]

QUESTION 2
2.1 Given: 0 ; -1 ; 1 ; 6 ; 14 ; . . .
2.1.1 Show that this sequence has a constant second difference. (2)
2.1.2 Write down the next term of the sequence. (1)
2.1.3 Determine an expression for the nth term of the sequence. (4)
2.1.4 Calculate the 30th term. (2)
2.2 In the arithmetic series: ? + ?? + ? + ?? + . . .
2.2.1 Prove that ? = 6 and ? = 20 . (2)
2.2.2 Determine which term of the series will be equal to 230. (3)
2.3 For which value(s) of k will the series: (3)
(1 − ?) + (1 − ?)²+ (1 − ?)³+ . . . converge?
    5             5             5
2.4 Given: 16 + 3 + 8 + 3 + 4 + 3 + 2 + . . .
2.4.1 Determine the sum of the first 40 terms of the series, to the nearest integer. (4)
2.4.2 Write the series: 16 + 8 + 4 + 2 + . . . in the form where ?^? = ??^?−1 and a and r are rational numbers. (2)
2.4.3 Determine ?∞ of the series in QUESTION 2.4.2. (2)
[25]

QUESTION 3
Given: ?(?) =   3     − 2
                    ? − 1
3.1 Write down the equation of the:
3.1.1 horizontal asymptote of f. (1)
3.1.2 vertical asymptote of f. (1)
3.2 Determine the x- and y-intercepts of f. (3)
3.3 Sketch the graph of f , showing clearly the asymptotes and the intercepts with the axes. (3)
3.4 If another function g is defined as g(x) = f (x – 3) + 7 , determine the coordinates of the point of intersection of the asymptotes of g. (2)
[10]

QUESTION 4
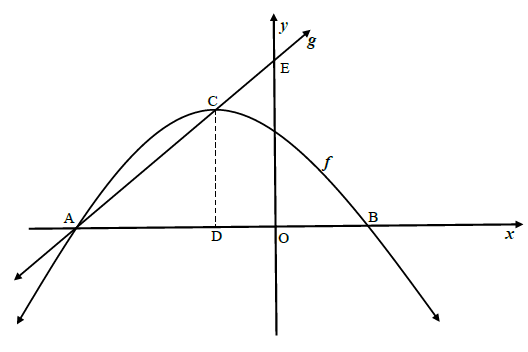
The functions ?(?) = −?2 − 2? + 3 and ?(?) = ?? + ? are drawn below, with g passing through E, C and A. A and B are the x-intercepts of f , and CD is the axis of symmetry of f . E is the y-intercept of g.

4.1 Determine the coordinates of C, the turning point of the graph of f . (3)
4.2 Determine the coordinates of A and B. (3)
4.3 Determine the values of m and c. (2)
4.4 Calculate the length of CE. (leave your answer in surd form) (3)
4.5 Determine the values of x, for which ?(?). ?(?) < 0 . (2)
[13]

QUESTION 5
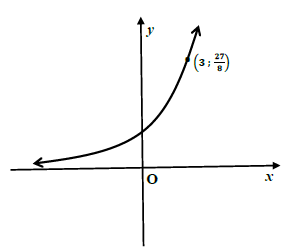
5.1 The graph of ?(?) = ?^?, where ? > 0 and ? ≠ 1, passes through the point (3 ; 27).
                                                                                                                                8

Use the sketch and the given information to answer the following questions.
5.1.1 Determine the value of ?. (2)
5.1.2 Write down the equation of ?−1 in the form y = . . . (2)
5.1.3 Determine the value(s) of x for which ?−1(?) = −1. (2)
5.1.4 If ℎ(?) = ?(? − 5) , write down the domain of ℎ. (1)
5.2 Draw a clear sketch graph of the function ? defined by the equation ?(?) = ?. ?? + ? , where ? < 0 ; ? > 1 and ? < 0. (a, b and q are real numbers). Indicate all the intercepts with the axes and the asymptotes. (3)
[10]

QUESTION 6
6.1 Jerry receives R12 000 to invest for a period of 5 years. He is offered an interest rate of 8,5% p.a. compounded quarterly.
6.1.1 Determine the effective interest rate. (3)
6.1.2 What is the amount that Jerry will receive at the end of the 5 years? (3)
6.2 A company bought office furniture that cost R120 000. After how many years will the furniture depreciate to a value of R41 611,57 according to the reducing-balance method, if the rate of depreciation is 12,4% p.a.? (4)
6.3 Andrew plans to save R20 000 for a deposit on a new car. He decided to use a part of his annual bonus to pay three even annual deposits into a savings account at the beginning of every year. Calculate how much money he must deposit to save up R20 000 after three years. Interest on the savings account is 8% p.a. compounded quarterly. (4)
[14]

QUESTION 7
7.1 Determine the derivative of ?(?) = 2?² − 3? from first principles. (5)
7.2 Determine ?? if ? = 2√? −3?
                        ??                   5?²
(4)
[9]

QUESTION 8
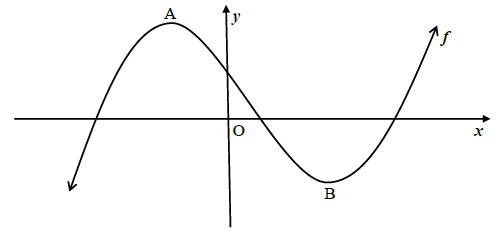
8.1 The graph of ?(?) = ?3 − 4?2 − 11? + 30 is drawn below. A and B are turning points of ?.

8.1.1 Determine the coordinates of A and B. (5)
8.1.2 Determine the x-coordinate of the point of inflection of ?. (2)
8.1.3 Determine the equation of the tangent to ? at ? = 2 , in the form ? = ?? + ?. (4)
8.1.4 Explain how the graph of ? can be shifted for it to have two equal roots. (2)
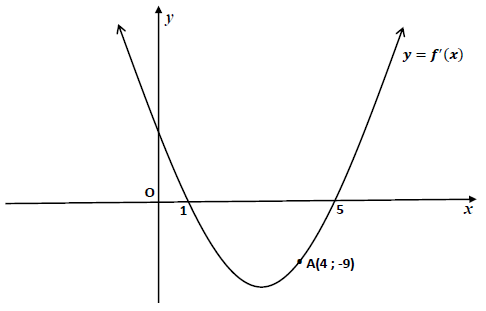
8.2 The diagram below shows the graph of ?′(?) , the derivative of ?(?) = ??³ + ??² + ?? + ?. The graph of ?′(?) intersects the x-axis at 1 and 5. A(4 ; – 9) is a point on the graph of ?′(?).

8.2.1 Write down the gradient of the tangent to ? at ? = 4. (1)
8.2.2 Determine the x-coordinates of the turning points of ?. (2)
8.2.3 For which value(s) of x is ? strictly increasing? (2)
[18]

QUESTION 9
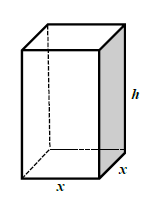
A solid square right prism is made of 8 ?³ melted metal. The length of the sides of the base are x metres and the height is ^h metres. The block will be coated with one layer of paint.

9.1 Express h in terms of x. (2)
9.2 Show that the surface area of the block is given by: ?(?) = 2?² +32      (3)
                                                                                                             ?
9.3 Calculate the dimensions of the block that will ensure that a minimum quantity of paint will be used. (5)
[10]

QUESTION 10
10.1 The events A and B are independent. P(A) = 0,4 and P(B) = 0,5. Determine:
10.1.1 P(A and B) (2)
10.1.2 P(A or B) (2)
10.1.3 P(not A and not B) (2)
10.2 Two identical bags are filled with balls. Bag A contains 3 pink and 2 yellow balls. Bag B contains 5 pink and 4 yellow balls. It is equally likely that Bag A or Bag B is chosen. Each ball has an equal chance of being chosen from the bag. A bag is chosen at random and a ball is then chosen at random from the bag.
10.2.1 Represent the information by means of a tree diagram. Clearly indicate the probability associated with each branch of the tree diagram and write down all the outcomes. (3)
10.2.2 What is the probability that a yellow ball will be chosen from Bag A? (1)
10.2.3 What is the probability that a pink ball is chosen? (3)
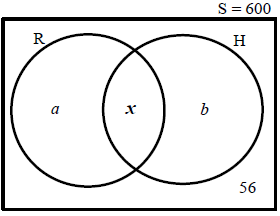
10.3 Eastside High School offers only two sporting activities, namely rugby (R) and hockey (H). The following information is given and partly represented in the diagram.

• There are 600 learners in the school.
• 372 learners play hockey.
• 288 learners play rugby.
• 56 of the learners play NO sport.
• The number of learners that play both hockey and rugby is x.

10.3.1 Write down the values of ? and ? in terms of x . (2)
10.3.2 Calculate the value of x . (2)
10.3.3 Are the events playing rugby and playing hockey mutually exclusive? Justify your answer. (1)
[18]

INFORMATION SHEET: MATHEMATICS