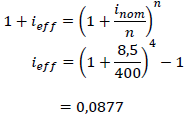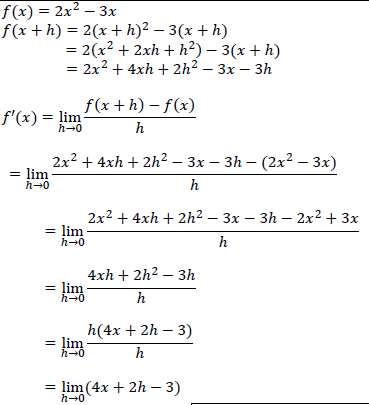GRADE 12 MATHEMATICS PAPER 1 MEMORANDUM - NSC PAST PAPERS AND MEMOS JUNE 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS P1
GRADE 12
JUNE 2016
MEMORANDUM
NATIONAL SENIOR CERTIFICATE
NOTE
- If a candidate answered a question TWICE, mark the FIRST attempt ONLY.
- Consistent accuracy(CA) applies in ALL aspects of the memorandum.
- If a candidate crossed out an attempt of a question and did not redo the question, mark the crossed-out attempt.
- The mark for substitution is awarded for substitution into the correct formula.
QUESTION 1
| 1.1.1 | 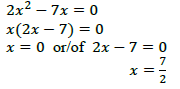 | ✓ factorisation ✓✓ ?-values (3) |
| 1.1.2 | ✓ standard form ✓ substitution ✓✓ ?-values (4) | |
| 1.1.3 | 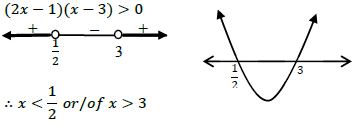 | ✓ critical values with method ✓✓ answer (3) |
| 1.1.4 | 3? . 3?+1 = 27? 32?+1 = 33? ∴ 2? + 1 = 3? ? = 1 | ✓ 32?+1 ✓ 33? ✓ equating ✓ answer(4) |
| 1.2 | 3 + ? = 2? If formula is used, award factor’s mark for substitution. | ✓ substitution ✓ removing brackets ✓ standard form ✓ factors ✓ ?-values ✓ ?-values (6) |
| 1.3 | ?(?) = (? − 2)(?2 − 6? + 10) Consider the quadratic factor : (?2 − 6? + 10) Δ = ?2 − 4?? = (−6)2 − 4(1)(10) = 36 − 40 = −4 => Δ < 0, therefor NO Solutions ? = 2 is the only solution. | ✓ substitution into delta ✓ answer ✓ conclusion (4) [23] |
QUESTION 2
| 2.1.1 | 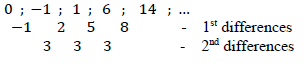 | ✓ first differences ✓ second differences (2) |
| 2.1.2 | Next term= 25 | ✓ answer(1) |
| 2.1.3 | 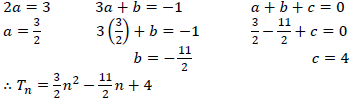 | ✓ ? = 3 2 ✓ ? = − 11 2 ✓ ? = 4 ✓ answer(4) |
| 2.1.4 | ?30 = 3 (30)2 −11(30) + 4 2 2 = 1189 | ✓ substitution (2) |
| 2.2.1 | ?3 − ?2 = ?4 − ?3 ? − 13 = 27 − ? 2? = 40 ? = 20 13 − ? = 7 ? = 6 | ✓ method ✓ values of a and b (2) |
| 2.2.2 | ? + (? − 1)? = ?? 6 + (? − 1)(7) = 230 7? = 231 ? = 33 | ✓ formula ✓ substitution ✓ answer (3) |
| 2.3 | ? =1 − ? 5 −1 < 1 − ? < 1 5 −5 < 1 − ? < 5 −6 < −? < 4 −4 < ? < 6 | ✓? = 1−? 5 ✓ substitution ✓ answer (3) |
| 2.4.1 | 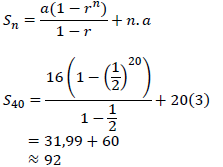 | ✓method ✓substitution ✓simplification ✓answer (4) |
| 2.4.2 | 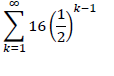 |
|
| 2.4.3 | ?∞ = ? 1 − ? 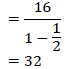 | ✓ substitution ✓ answer (2) [25] |
QUESTION 3
| 3.1.1 | ? = −2 (horizontal asymptote ) | ✓ answer(1) |
| 3.1.2 | ? = 1 (vertical asymptote) | ✓ answer(1) |
| 3.2 | 3 − 2 = 0 | ✓ y = 0 ✓ x – intercept ✓ y – intercept (3) |
| 3.3 | 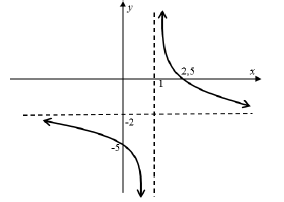 | ✓ asymptotes ✓ x-and y-intercepts ✓shape (3) |
| 3.4 | (4 ; 5) | (2) |
| [10] |
QUESTION 4
| 4.1 | 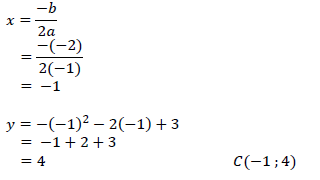 | ✓ ? -coordinate ✓y-coordinate ✓coordinates of C (3) |
| 4.2 | −?2 − 2? + 3 = 0 ?2 + 2? − 3 = 0 (? + 3)(? − 1) = 0 ? + 3 = 0 ?? ? − 1 = 0 ? = −3 ?? ? = 1 ?(−3; 0) ?(1; 0) | ✓standard form ✓factors ✓ both values (3) |
| 4.3 | m = 2 & c = 6 y = 2? + 6 | ✓value of m ✓value of c (2) |
| 4.4 | 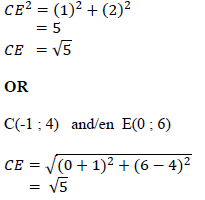 | ✓method ✓substitution ✓answer (3) |
| 4.5 | ?> 1 | ✓✓answer (2) |
| [13] |
QUESTION 5
| 5.1.1 | 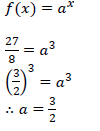 | ✓substitution ✓answerd (2) |
| 5.1.2 | 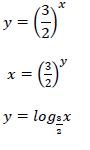 | ✓swop ? and ? ✓ answer (2) |
| 5.1.3 | 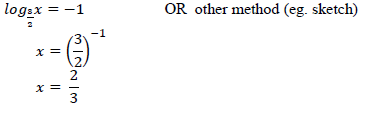 | ✓equating ✓answer (2) |
| 5.1.4 | ? ∈ R | answer(1) |
| 5.2 | 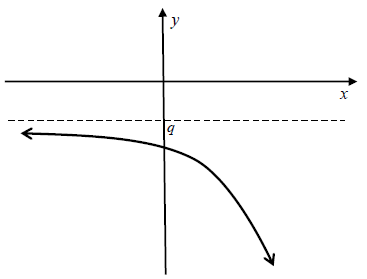 | ✓asymptote ✓negative y-intercept ✓shape (3) |
| [10] |
QUESTION 6
| 6.1.1 | effective rate = 8,77%p.a | ✓ formula ✓ substitution ✓ answer (3) |
| 6.1.2 | 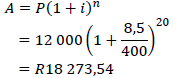 | ✓formula ✓substitusie ✓answer(3) |
| 6.2 | 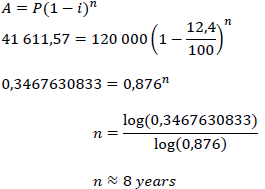 | ✓substitution ✓simplification ✓correct use of logs ✓answer (4) |
| 6.3 | 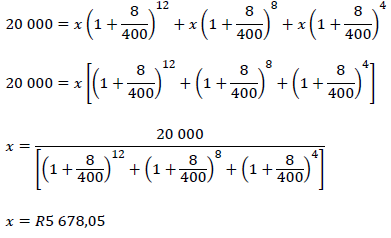 | ✓✓ setting up equation ✓ x the subject of the formula ✓ answer (4) |
[14]
QUESTION 7
| 7.1 | = 4? - 3 Answer ONLY: 0 marks | ✓ substitute (? + ℎ) Penalise 1 mark for incorrect use ✓ simplification
|
| 7.2 | 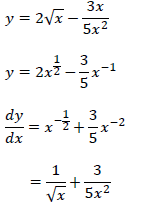 | Penalise 1 mark for incorrect notation
|
[9]
QUESTION 8
| 8.1.1 | ?(?) = ?3 − 4?2 − 11? + 20 ?′(?) = 3?2 − 8? − 11 = 0 (3? − 11)(? + 1) = 0 3? − 11 = 0 ?? ? + 1 = 0 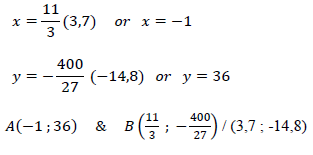 | ✓ ?′(?) = 0 ✓ factors ✓ x-values ✓ y-values ✓ coordinates (5) |
| 8.1.2 | ?′′(?) = 6? − 8 = 0 6? = 8 ? =8 or/of 1 1 or/of 1, 33 6 3 OR 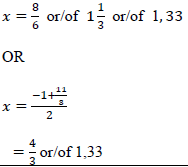 | ✓ ?′′(?) = 0 ✓ answer (2) |
| 8.1.3 | ? = ?′(2) = 3(2)2 − 8(2) − 11 = −15 ?(2) = (2)3 − 4(2)2 − 11(2) + 30 = 0 ? − ?1 = ?(? − ?1) ? − 0 = −15(? − 2) ? = −15? + 30 | ✓ ? = −15 ✓ ?(2) = 0 ✓ substitution ✓ answer (4) |
| 8.1.4 | 36 units downwards 14,8 units upwards | ✓ answer ✓ answer (2) |
| 8.2.1 | ? = −9 | ✓ answer (1) |
| 8.2.2 | ? = 1 ?? ? = 5 | ✓✓ answers (2) |
| 8.2.3 | ? <1 or ? > 5 | ✓ ? < 1 ✓ ? > 5 (2) |
[18]
QUESTION 9
| 9.1 | ? = ?2ℎ 8 = ?2ℎ ∴ ℎ = 8 ?2 | ✓substitution ✓answer (2) |
| 9.2 | ? = 2?2 + 4?ℎ No mark for the answer | ✓ 2?2 ✓ 4?ℎ ✓ substitution (3) |
| 9.3 | ?(?) = 2?2 + 32?−1 ?′(?) = 4? − 32?−2 = 0 4?3 − 32 = 0 4?3 = 32 ?3 = 8 = 23 ∴ ? = 2 | ✓ ?′(?) = 0 ✓ standard form ✓exponential law ✓ value of x ✓ dimensions (5) |
[10]
QUESTION 10
| 10.1.1 | ?(? and ?) = ?(?) × ?(?) = 0,4 × 0,5 = 0,2 | ✓ rule ✓ answer(2) |
| 10.1.2 | ?(? or ?) = ?(?) + ?(?) − ?(? and?) = 0,4 + 0,5 − 0,2 = 0,7 | ✓ rule ✓ answer(2) |
| 10.1.3 | ?(??? ? and ?) = 1 − ?(? or ?) = 1 − 0,7 = 0,3 | ✓ rule ✓ answer (2) |
| 10.2.1 | 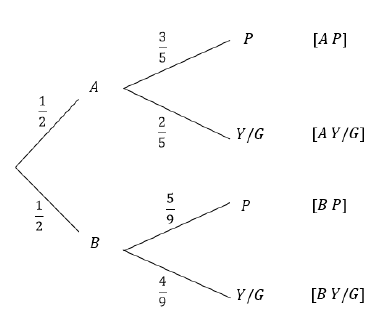 | ✓ first branch If probabilities not listed, maximum 1 mark |
| 10.2.2 | ?(?????? from ??? ?)= 2 5 | ✓answer (1) |
| 10.2.3 | ?(????) = 3 + 5 10 18 = 26 45 (0,58) | ✓ 3 10 ✓ 5 18 ✓answer (3) |
| 10.3.1 | ? = 288 − ? ? = 372 − ? | ✓ answer ✓ answer (2) |
| 10.3.2 | 288 − ? + ? + 372 − ? + 56 = 600 −? = −116 ? = 116 | ✓ equation ✓ answer (2) |
| 10.3.3 | No P(A and B) ≠ 0 | ✓ answer (1) [18] |
| TOTAL: 150 |

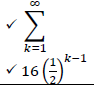 (2)
(2)