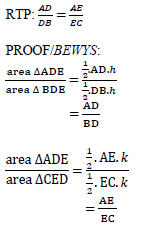
GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS JUNE 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS P2
GRADE 12
JUNE 2016
NATIONAL SENIOR CERTIFICATE
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining the answers.
- Answers only will not necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and nongraphical), less stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Number the answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly.
QUESTION 1
The table below shows the amount of time (in hours) that learners aged between 12 and 16 spent playing sport during school holidays.
| Time (hours) | Cumulative Frequency |
| 0 ≤ t < 20 | 30 |
| 20 ≤ t < 40 | 69 |
| 40 ≤ t < 60 | 129 |
| 60 ≤ t < 80 | 157 |
| 80 ≤ t < 100 | 167 |
| 100 ≤ t < 120 | 172 |
1.1 Draw an ogive (cumulative frequency curve) in the SPECIAL ANSWER BOOK provided to represent the data above. (4)
1.2 Write down the modal class of the data. (1)
1.3 How many learners played sport during the school holidays, according to the data above? (1)
1.4 Use the ogive (cumulative frequency curve) to estimate the number of learners who played sport more than 60% of the time. (2)
1.5 Estimate the mean time (in hours) that learners spent playing sport during the school holidays. (4)
[12]
QUESTION 2
According to an official in the quality assurance department of a can manufacturing business, the standard deviation of a 340 ml can is 2,74 ml. Out of a sample of 20 cans the following content was measured.
342 338 336 340 340 345 334 338 339 340
341 337 336 340 335 336 342 340 337 336
2.1 Determine the mean volume of these 20 cans. (2)
2.2 Determine the standard deviation of these 20 cans. (2)
2.3 Determine what percentage of the data is within one standard deviation of the mean. (2)
[6]
QUESTION 3
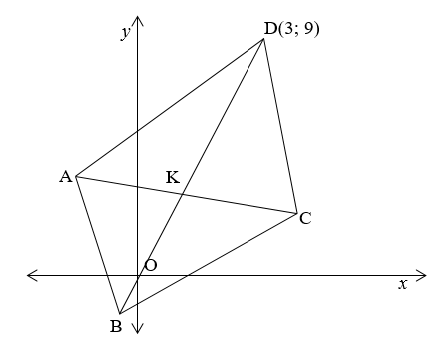
In the diagram, A, B, C and D are the vertices of a rhombus.
The equation of AC is ? + 3? = 10.
3.1.1 Show that the equation of BD is 3? − ? = 0. (3)
3.1.2 Calculate the coordinates of K, the point of intersection of AC and BD. (4)
3.1.3 Determine the coordinates of B. (3)
3.1.4 Calculate the coordinates of A and C if AD = √50. (8)
3.2 P(-3;2) and Q(5;8) are two points in a Cartesian plane.
3.2.1 Calculate the gradient of PQ. (2)
3.2.2 Calculate the angle that PQ forms with the positive ?-axis, correct to one decimal place. (2)
3.2.3 Determine the equation of the straight line parallel to PQ that intercepts the x-axis at (8; 0). (3)
[25]
QUESTION 4
In the diagram the two circles of equal radii touch each other at point D(p;p). Centre A of the one circle lies on the y-axis. Point B(8; 7) is the centre of the other circle. FDE is a common tangent to both circles.
4.1 Determine the coordinates of point D. (2)
4.2 Hence, show that the equation of the circle with centre A is given by ?2 + ?2 − 2? − 24 = 0. (5)
4.3 Determine the equation of the common tangent FDE. (5)
4.4 Point B(8;7) lies on the circumference of a circle with the origin as centre. Determine the equation of the circle with centre O. (2)
[14]
QUESTION 5
5.1 Simplify (WITHOUT THE USE OF A CALCULATOR)
sin(180° − ?). cos(? − 360°). tan(180° + ?). cos(−?)
tan(−?). cos(90° − ?). sin(90° − ?)
(8)
5.2 Prove the identity: sin ? + 1 + cos ? = 2
1+cos ? sin ? sin ?
(5)
5.3 Use compound angles to show that: cos 2? = 2???2? − 1 (2)
5.4 Determine the general solution for x if: cos 2? + 3 sin ? = 2 (7)
5.5 In ΔABC: Â + B̂ = 90°. Determine the value of sin A . cos B + cos A . sin B. (3)
[25]
QUESTION 6
The functions of ?(?) = −tan 1? and ?(?) = cos(? + 90°) for −180° ≤ ? ≤ 180° are given.
2
6.1 Make a neat sketch, on the same system of axes of both graphs on the grid provided in the SPECIAL ANSWER BOOK. Indicate all intercepts with the axes and coordinates of the turning points. (6)
6.2 Give the value(s) of x for which: cos(? + 90°) ≤ −tan1? (2)
2
[8]
QUESTION 7
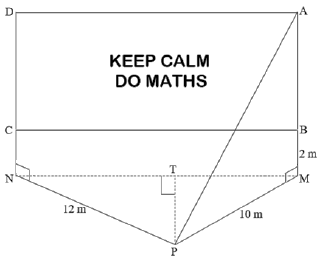
In the figure, ABCD represents a large rectangular advertising board. A surveyor, standing at the point P, is in the same horizontal plane as the bottom of the uprights holding the board. AM and DN are perpendicular to ΔPMN. Also, BM = 2 m, PM = 10 m, PN = 12 m, AP̂M = 35° and MP̂N = 126,9°.
7.1 Calculate the length of AB. (3)
7.2 Calculate how far the surveyor is from the board. (Length of PT) (4)
[7]
Give reasons for ALL statements in QUESTIONS 8, 9, 10 and 11.
QUESTION 8
8.1 Complete the following: The opposite angles of a cyclic quadrilateral are … (1)
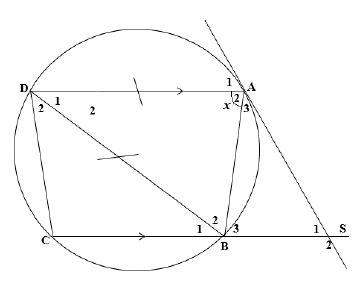
8.2 In the diagram, EF and EG are tangents to circle with centre O. FH || EK, EK intersects FG at J and meets GH at K. Ĥ = ?.
Prove that …
8.2.1 FOGE is a cyclic quadrilateral. (5)
8.2.2 EG is a tangent to the circle GJK. (5)
8.2.3 FÊG = 180° − 2?. (3)
[14]
QUESTION 9
ABCD is a cyclic quadrilateral. AS is a tangent. CBS is a straight line. AD || SC and AD = BD.
9.1 Name, with reasons, FIVE other angles each equal to x. (5)
9.2 Prove that ASCD is a parallelogram. (4)
9.3 Name a triangle in the figure similar to ΔADB. (1)
9.4 Hence prove that: SC.SB = DC2. (5)
[15]
QUESTION 10
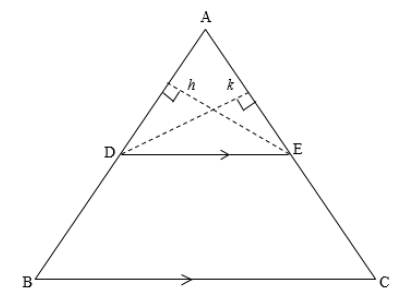
10.1 In the diagram below, ΔABC is drawn with DE || BC.
10.1.1 Complete the following statement: A line drawn parallel to one side of a triangle divides the other two sides in … (1)
10.1.2 Use QUESTION 10.1.1 to prove that: ??=??
?? ??
(5)
10.2 In ΔPQR, T is a point on PQ, V is a point on PR and TVRW is a parallelogram. PT = x + 2 units, QW = x + 4 units, QT = 15 units and WR = x units.
10.2.1 Calculate the value of x. (6)
10.2.2 If VR = 18 units and x > 1, determine the length of PV. (3)
[15]
QUESTION 11
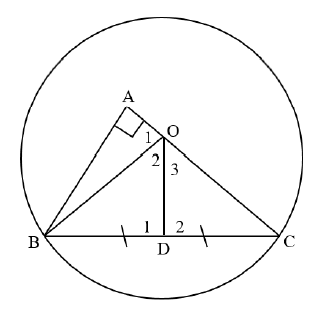
Given O is the centre of the circle. BA ⊥ AC. D is the midpoint of BC.
11.1 Prove that: ΔABC ||| ΔDOC (3)
11.2 Show that: OC = DC.BC
AC
(1)
11.3 Given: DC = 15 cm and AB = 18 cm. Calculate the length of OC, rounded off to one decimal unit. (5)
[9]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS