Monday, 24 May 2021 06:32

GRADE12 MATHEMATICS PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS JUNE 2016

More in this category: « GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS JUNE 2016 PHYSICAL SCIENCES PHYSICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS JUNE 2016 »
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

MATHEMATICS P2 
GRADE12
JUNE2016
MEMORANDUM
NATIONAL SENIOR CERTIFICATE

QUESTION

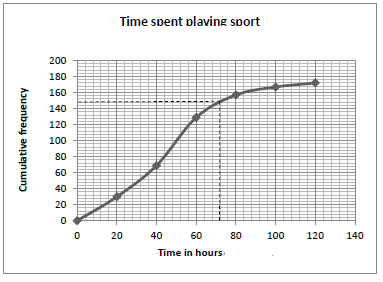
 1.1
Time (hours)  Cumulative Frequency 
0 ≤ t < 20  30
20 ≤ t < 40  69
40 ≤ t < 60  129
60 ≤ t < 80  157
80 ≤ t < 100  167
100 ≤ t < 120  172

 

1.1 new

 (4) 
1.2 40 ≤ t < 60 ✓answer (1)
1.3 172 ✓answer (1)
1.4  (72;148)
∴ 172-148 = 24 learners		 ✓148
✓24
(2)
1.5   Frequency: 30; 39; 60;28;10;5
30×10+39×30+60×50+28×70+10×90+5×110=7880
                                 172
=7880
   172
=45,81		 ✓frequency
✓midpoints
✓7880
    172
✓answer(4)

[12]

QUESTION 2

 2.1 𝑥̅= 6772 
       20
𝑥̅=338,6 𝑚𝑙		  ✓ 𝑥̅= 6772 
            20
✓answer(2)
 2.2  2,71 ml ✓✓ answer
(2)
 2.3 [338,6 – 2,71; 338,6 + 2,71]
[335,89; 341.31]		 ✓✓ interval
(2)

[6]

QUESTION 3

 3.1

𝑚𝐴𝐶= −1   
            3
𝑚𝐵𝐷=3 [Diagonals of a rhombus]
𝑦− 𝑦1=𝑚(𝑥− 𝑥1)

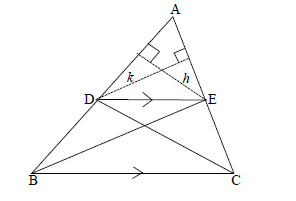
𝑦−9=3(𝑥−3)

3𝑥−𝑦=0 

 ✓S
✓R
✓ subst, m = 3 & (3;9) in eqn. 
(3) 
 3.1.2

𝑥+3𝑦=10……… .(1)

3𝑥−𝑦=0 …………(2)
3𝑥+9𝑦=30………(3) (1)×3
10 𝑦=30 (3)−(2)
𝑦 =3

𝑥+3(3)=10

𝑥=1
K(1; 3)

 ✓equating two eqns
✓simplification
✓y = 3
✓x = 1
(4)
 3.1.3 3.13 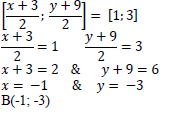✓method using midpoint 
✓ simplification
✓ coordinates of B 
(3)
 3.1.4

 AD =√(3−𝑥)2+ (9−𝑦)2

∴ √50= √9−6𝑥+𝑥2+81−18𝑦+ 𝑦2

∴ 50= 𝑥2−6𝑥+𝑦2−18𝑦+90
But:𝑥=10−3𝑦

∴ (10−3𝑦)2−6(10−3𝑦)+ 𝑦2−18 𝑦+90=50

∴ 100−60𝑦+9𝑦2−60+18𝑦+𝑦2−18𝑦+90=50
∴10𝑦2−60𝑦+80=0
∴ 𝑦2−6𝑦+8 =0
∴ (𝑦−4)(𝑦−2) =0
𝑦=4   or 𝑦= 2
𝑥=10−3(4) or 𝑥=10−3(2)
𝑥= −2                  or 𝑥=4
A(-2;4) C(4; 2)

 ✓ subst into eqn dist AD 
✓ subst
AD = √50
✓subst
x =10 - 3y
✓ simplification
✓standard form
✓values for y
✓values for x
✓coordinates
(8)
 3.2.1

 𝑚PQ= 8 - 2=   6
           5−(−3)   8

= ¾

 ✓ subs into eqn 
✓ answer
(2)
 3.2.2 tan𝜃= ¾ 𝜃=36,9

✓ tan 𝜃 

✓ answer
(2)
 3.2.3

 𝑦=¾𝑥+𝑐

0= ¾(8)+𝑐

𝑐= −6

𝑦= ¾𝑥−6

✓subst. m = 34
✓ subst. (8:0)

✓ answer
(3)

[25]

QUESTION 4

4.1 

A(0; y)

∴𝑝= 0+8=4

         2

∴D(4;4)

 ✓midpt equation
✓coordinates of D
(2)
4.2 

Ay = 𝑦+7=4
          2

A(0; 1)2

∴(𝑥−0)2+(𝑦−1)2= 𝑟2

∴(4−0)2+(4−1)2= 𝑟2

∴16+9= 𝑟2

∴𝑥2+(𝑦−1)2=25

∴𝑥2+ 𝑦2−2𝑦−24=0

 ✓ y-coordinate of A
✓ A(0; 1)
✓✓subst (0;1)and (4;4)
into equation.
✓r2
(5)
 4.3

 𝑚𝐴𝐵×𝑚𝐹𝐷𝐸= −1 [tan radius]

✓S/R
✓mAB ¾
✓ 𝑚𝐹𝐷𝐸 = -4 

              3

✓subst m and (4;4) into eqn
✓answer
(5)
 4.4

 𝑥2+ 𝑦2= 𝑟2

(8)2+(7)2= 𝑟2

∴𝑥2+ 𝑦2=113

 ✓subst (8;7) into eqn
✓answer
(2)

[14]


QUESTION 5

5.1.1 

=sin𝑥.cos𝑥.tan𝑥.cos𝑥
    sin𝑥.cos𝑥.(−𝑡𝑎𝑛𝑥)
= −cos𝑥 

 ✓sin x
✓cos x
✓tan x
✓cos x
✓sin x
✓cos x
✓-tan x
✓-cos x
(8) 
 5.2

   sin𝑥   + 1 + cos𝑥 =    2   
1+cos𝑥        sin𝑥        sin𝑥
LHS:sin2𝑥 + (1+cos𝑥)(1+cos𝑥)
                  sin𝑥(1+cos𝑥)
  sin2𝑥 + 1 + 2cos𝑥2𝑥)
       sin𝑥(1+cos𝑥)

   2+2cos𝑥
 sin𝑥(1+cos𝑥) 
     2(1+1cos𝑥)
   sin𝑥(1+1cos𝑥)

   2   
 sin𝑥

= RHS/RK

 ✓ denominator
✓ numerator
✓ simplification 
✓ identity
✓ factorisation
(5)
 5.3  cos2𝑥=cos(𝑥+𝑥)
= cos𝑥.cos𝑥−sin𝑥.sin𝑥
=cos2𝑥−sin2𝑥
= cos2𝑥−(1−cos2𝑥)
=2cos2𝑥−1		 ✓ expansion
✓ identity
(2)
 5.4

cos2𝑥+3sin𝑥=2

1−2sin2𝑥+3sin𝑥=2

2sin2𝑥−3sin𝑥+1=0

(2sin𝑥−1)(sin𝑥−1)=0
2sin𝑥=1 or sin𝑥−1=0
sin𝑥= ½ or sin𝑥=1
𝑥=30°+𝑛.360 𝑥=90°+𝑛.360
𝑥=150+𝑛.360 ; 𝑛 ∈𝒁

 ✓ identity
✓ standard form 
✓factors
✓ sin x = ½
sin x = 1 (both eqns)
✓ x = 30°
✓ x = 150°
✓ x = 90°
(7)
5.5 sin𝐴cos𝐵+cos𝐴sin𝐵=sin(𝐴+𝐵)
= sin90°
= 1		 ✓ identity
✓ subst
✓ answer
(3)

[25]

QUESTION 6

6.1   6.1 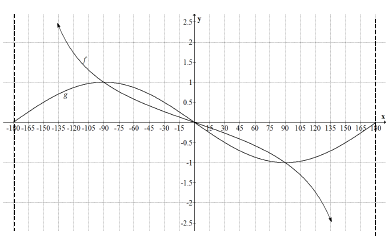✓shape g
✓intercepts
✓min & max value
✓shape f
✓asymptotes
✓ intercept
(6) 
 6.2 −180°<𝑥≤−90° or/of 0°≤𝑥≤90°  ✓critical values 
✓ notation
(2)

Related Items

[8]


QUESTION 7

7.1  MN2=PN2+PM2−2PN.PMcos MP̂N
= 122+102−2(12)(10)cos126,9°
=144+100−240(−0,6)
=388,1
MN=19,7 𝑚
MN=AD=19,7 𝑚 		 ✓ correct subst into cos rule 
✓ simplification 
✓ answer 
(3) 
 7.2

½MN.PT= ½PN.PMsinMP̂N [Both equal Area of ΔPMN]
½(10)PT= ½(12)(10)sin126,9°

PT=12.sin126,9°
PT = 9,596 m
= 9,6 m

 ✓ Equating Area form 
✓ correct subst 
✓ simplification 
✓ answer 
(4)

[7]


QUESTION 8

8.1  Supplementary ✓ answer (1)
 8.2.1

EF̂O=90° [tan radius]
EĜO=90° [tan radius]

EF̂O+EĜO=180°
∴FOGE is cyclic quad [opp angles supplementary]

 ✓ S ✓R
✓S ✓R
✓ R
(5)
 8.2.2 Ĝ1= Ĥ=𝑥 [ tan chord]
K̂1= Ĥ=𝑥 [ corresp angles; EK || FH] ∴Ĝ1= K̂1
EG is a tangent [angle between line and chord]		 ✓S ✓R
✓S ✓R
✓R
(5)
 8.2.3 Ô1=2Ĥ [ angle at centre]
= 2x
∴FÊG=180°−2𝑥 [ opp angles of cyclic quad]		 ✓S ✓R
✓R
(3)

[14]


QUESTION 9

 9.1 B̂2 = Â2 = x [ angles opp equal sides]
Â1 = B̂2 = x [ tan chord]
Ŝ1 = Â1 = x [ corresp; AD||SC]
𝐵̂3 = 𝐴̂2 = x [ alt int; AD|| SC]
AD̂C = B̂3 = x [ ext angle of cyclic quad]		 ✓ S/R
✓ S/R
✓ S/R
✓ S/R
✓ S/R
(5) 
 9.2 Â1 = AD̂C [ from 8.1]
AS || DC [alt angles equal]
DA || CS [given]
ASCD is a parallelogram [opp sides ||]		 ✓ S
✓ S/R
✓ S
✓ R
(4)
 9.3  ΔSAB ||| ΔADB [ A,A,A]/[H,H,H] ✓ ΔSAB
(1)
 9.4

SA = SB  [from 8.3.1]
AD    AB

∴AD.SB=SA.AB
ButAD = SC [ ASCD is a parallelogram]
and AB = SA[sides opp equal angles]
= DC [ASCD is a parallelogram] ∴ SC.SB=DC2

 ✓ S
✓ S
✓ S/R
✓ S/R
✓ R
(5)

[15]

QUESTION10

10.1.1   In proportion ✓ Answer (1)

10.1.2

 

 10.12B

RTP:10.12

PROOF:

10.12C

But Area ΔBDE=Area Δ CED (same base and same height)

∴ areaΔADE =   area ΔADE 
   area ΔBDE =  area Δ CED
∴  AD =   AE 
    DB =   EC

 ✓ ratio of area of
ΔADE: ΔBDE
✓AD  
   BD
✓ratio of area of
ΔADE : ΔCED
✓AE
   EC
✓equating two areas(5)
10.2.1

QT=QW
TP   WR

prop thm; TW || VR

∴  15   = 𝑥+4 
   𝑥 + 2     𝑥
𝑥2+6𝑥+8=15𝑥

𝑥2−9𝑥+8=0

∴(𝑥−8)(𝑥−1)=0

∴𝑥=8 or 𝑥=1

 ✓QT=QW
   TP   WR
✓R
✓ substitution 
✓ std form
✓factors
✓ both values for x
(6)
 10.2.2

 PV = PT  prop thm TV || QR
 VR = TQ

PV = 10 
18 =  15

PV = 12units

 ✓ S/R
✓ substitution 
✓ answer
(3)

[15]


QUESTION11

11.1 

𝐷2=90° [ line from centre to midpoint of chord]
In Δ ABC & Δ DOC
i) Â= D2 [ both equal to 90°]
ii)Ĉ= Ĉ [common]

∴ΔABC |||ΔDOC [AAA/𝐻𝐻𝐻]

 ✓ S/R
✓ S/R
✓ S
(3) 
11.2

OC = DC  ΔABC |||ΔDOC
BC     AC

OC = DC.BC 
             AC

 

 ✓ S/R
(1)
11.3

 AC2=BC2−AB2 [Pythagoras]
= 302−182
= 576
AC = 24 cm

𝑂𝐶=𝐷𝐶.𝐵𝐶

         𝐴𝐶

= 15 × 30=18,8 𝑐𝑚

        24

 ✓ S/R
✓ subst in eqn 
✓ AC = 24
✓ subst 
✓ answer
(5)

[9]

TOTAL: 150

Last modified on Tuesday, 15 June 2021 08:04
Published in Grade 12 2016 June Exams, Past Papers

Related items

More in this category: « GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS JUNE 2016 PHYSICAL SCIENCES PHYSICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS JUNE 2016 »
back to top