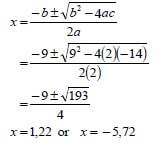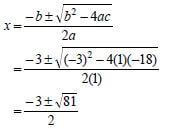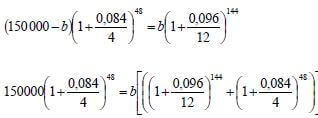1.1.1

(3x −1 )(x + 4)= 0
x = 1  or x = −4
      3

✓ x = 1
          3 
✓ x=−4 (2)

1.1.2

2x² +9x−14 = 0

OR

x =1,22 or        x = −5,72

✓ substitution into correct formula
✓simplification
✓  x =1,22
✓   x = −5,72 (4)

OR

✓ for adding 81 on both sides
                    16
✓  simplification
✓  x =1,22
✓  x = −5,72                     (4)

1.1.3

√3 − 26x = 3x
3 − 26x = 9x²
9x² + 26x −3 = 0
(9x−1)(x+3)= 0
x = 1  or x = −3
      9
N/A

✓ 3 − 26x = 9x²
✓ standard form
✓  factors
✓ answer with selection  (4)

1.1.4

(x −1 )(x − 4)> x +11
x² −5x + 4 > x +11
x² − 6x − 7 > 0
(x −7)(x +1)> 0

x < −1 or x > 7

✓ x² −5x + 4
✓ standard form
✓ factors
✓✓  x < −1 or x > 7 (5)

1.2

4√x⁷ - 5√x⁷
     √x
= -√x⁷
    √x
= - x^7/₂
     x^½
= −x³

OR

√x⁷(4−5)
      √x
= √x⁶ (−1)3

= −x³

OR

✓ 4√x⁷ - 5√x⁷
✓ -√x⁷
✓−x³ (3)

OR

✓ √x⁷(4−5)
✓ √x⁶ (−1)3
✓ −x³(3)

OR

✓ 4x^7/₂ - 5x^7/₂
✓ -x^7/₂
✓ −x³ (3)

1.3

x−2y−3=0
x = 2y+3 ................(1)
xy = 9  ................  (2)
Substitute (1) into (2)
(2y +3)y =9
2y² +3y =9
2y² +3y −9 = 0
(2y −3)(y +3)= 0
y = 3 or y = −3
      2
x = 6 or x = −3

OR

y = x - 3 ................  (1)
        2
xy = 9  ................  (2)
Substitute (1) into (2)
  x[ x−3] = 9
    [  2   ]
x² −3x =18
x² −3x −18 = 0
(x − 6)(x + 3) = 0
x=6 or x= −3
y= 3 or y = −3
     2

OR

x−2y−3=0
x = 2y+3  ......................... (1)
y= 9  .........................(2)
     x
Substitute (2) into (1)

x = 2[9] +3
        [x]
x² − 2(9)−3x = 0
x² −3x −18 = 0

x = 6  or x = - 3
y= 9 =1,5     or y = 9  = −3
     6                     −3

✓ x=2y+3
✓ substitution
✓ standard form
✓ y-values
✓  x-values                         (5)

OR

✓ y = x -3 
            2
✓ substitution
✓ standard form
✓  x-values
✓  y-values                         (5)

OR

✓ y = 9
          x
✓ substitution
✓ standard form
✓ x-values
✓  y-values                         (5)

1.4

x² + 2xy + 2y²
=x² + 2xy + y² +y²
=  (x+ y)² + y²
(x+y)² ≥ 0 and y² ≥ 0
Therefore (x+y)² +y² ≥ 0

✓  x² + 2xy + y² +y²
✓ (x+ y)²
✓  (x+y)² ≥ 0 and y² ≥ 0
✓ (x+y)² +y² ≥ 0 (4) [27]

2.1.1

37;  50

✓  37
✓  50                                 (2)

2.1.2

a = second difference = 2  =1
                  2                  2
3a+b = 5
3+b = 5
b = 2
a +b + c = 5
1+ 2+c = 5
c = 2
T_n = an² +bn+c
= n² + 2n+ 2

✓  second difference of 2
✓  a =1
✓  b = 2
✓  c = 2 (4)

2.1.3

n² + 2n + 2 =1765
n² + 2n −1763 = 0
(n + 43)(n − 41)= 0
n = −43 or n = 41
N/A

OR

n² +2n+2 =1765
n² +2n−1763= 0

n = −43 or n = 4
N/A

✓  equating T_n to 1765
✓  standard form
✓  factors
✓  answer with rejection (4)

OR

✓  equating T_n to 1765
✓  standard form
✓  subt in correct formula
✓  answer  with rejection (4)

2.2

Sum of multiples of 7 from 35 to 196:
a = 35;   d = 7
S_n = n  [a + ℓ ]
        2
= 24 [ 35+196]
    2
= 12[231]
= 2772

Sum of all natural numbers from 35 to 196:
a = 35;  d = 1;  n = 162
S_n = n [a + ℓ]
        2
= 162 [ 35+196]
    2
=81[231]
= 18 711
Sum of numbers not divisible by 7
= 18 711 - 2772
= 15 939

✓  correct a, d and n substitution into correct formula
✓  answer
✓  162
✓  answer
✓  answer                          (5)  [15]

3.1

r = 0,94; a =100
T₃ = ar²
=100(0,94)²
=88,36 km

✓ r = 0,94
✓ answer                          (2)

3.2

S_n = a(rⁿ −1 )
           r −1
750 = 100(0,94ⁿ −1 )
                 0,94−1
750( −0,06)  = 0,94ⁿ −1
     100
0,94ⁿ =1− 9 or [47]n = 11
                20    [50]      20
0,94ⁿ    = 0,55
n = log 0,55
      log 0,94
= 9,66

He will pass the halfway point on the 10^th day

✓ substitution into correct formula
✓ 0,94ⁿ  = 0,55
✓ use of logarithms
✓ answer (4)

3.3

S∞ =    a    
         1− r
1500 <  100   
            1− r
1− r <  100   
          1500
r > 14 or 93,33%
     15

✓ use of S_∞ formula
✓ substitution
✓  answer (3) [9]

4.1

0< x ≤1 or (0 ;1]

✓✓ answer (2)

4.2

p = log_⁴/3 ¹⁶/₉
[4]^p = 16
[3]       9

[4]² = [4]
[3]      [3]
p=2

✓  substitution
✓✓ [4]²
       [3]
✓  answer (3)

4.3

f : y = log_⁴/3 x
f ^-1 : x = log_⁴/3 y
y = [4]^x  
      [3]

✓ x = log _⁴/3 y

✓ y = [4]^x   (2)
          [3]

4.4

y > 0   or     y∈(0;∞)

✓✓  answer (2)

4.5

[−2 ; ¹⁶/₉]

✓ -2
✓ 16   (2) [11]
     9

5.1

x∈R; x ≠ −1

✓ x∈R
✓  x ≠ −1 (2)

5.2

x-intercept of  f:
0 =  2   + 4
     x+1
    2    =  − 4
 x + 1
2 = -4x - 4
4x = −6
x = −³/₂

✓ equating to 0
✓ answer  (2)

5.3

y =      2    + 4
         x+1
14 =   2    + 4
3      k +1
  2    =  14 −4
k+1       3
    2   =  2  
 k +1     3
2k + 2= 6
k +1= 3
k = 2

✓ substitution
✓ simplification
✓  answer (3)

5.4

C(2; 4)

✓ 2
✓ 4  (2)

5.5

y = a(x + p)² + q
= a(x −2)² + 4
Substitute (0 ; 0):
0 = a(0− 2)² + 4
0 = 4a + 4
a =−1
y =−(x −2)² + 4

✓ a(x−2)² +4
✓ Substitute (0 ; 0)
✓ a = −1  (3)

5.6

x≤− 3 or −1<x < 0 or x > 4
       2

✓ x ≤ − ³/₂
✓✓  −1< x < 0
✓  x > 4  (4)

5.7

2 − 5:  f  shifted 1 unit to the right and 9 units down.
x
− ( x -  3)² -  5:  g  shifted 1 unit to the right and 9 units down.
Therefore the shift of both graphs took place relative to each other
They only intersect in the third quadrant.
Therefore there is only one point of intersection.

✓ both shifted 1 unit to the right
✓  both shifted 9 units down
✓  relative shift
✓  one real root (4) [20]

6.1

A = P(1−i)ⁿ
0,5P = P( 1 - 0,15)ⁿ
(1 - 0,15)ⁿ =  0,5
(0,85)ⁿ =  0,5
n =   log0,5  or log_0,855,5
       log0,85
= 4,27 years

✓ A = 0,5P
✓ substitution into correct formula
✓ use of logs
✓ answer (4)

6.2

In account one month before his 55^th birthday:

=3 478620,49
In account on his 55^th birthday:
A = P(1+i)
3 478620,49 [1 + ^0,092/₁₂]¹
= R3505289,91

OR

= R3505289,91

✓ value of i
✓ value of n
✓ substitution into  correct formula
✓ adding last month's interest
✓ answer (5)

OR

✓ value of i
✓ value of n
✓ substitution into  correct formula
✓ adding last month's interest
✓ answer (5)

6.3

Invest  Rx  in account A paying 8,4% p.a. compounded quarterly.
A = P(1+i)n
= x [1 + ^0,084/₄]⁴⁸
= 2,711662406x
Invest (R150 000 - x) in Account B paying 9,6% compounded monthly.
After 12 years, the amounts are equal:
= x [1 + ^0,084/₄]⁴⁸ =  (150000 - x)(1 + ^0,096/₁₂)¹⁴⁴
2,711662406x = 3,150044027(150000− x)
2,711662406x = 472506,6041−3,150044027x
5,861706433x = 472506,6041
x = R80 609,05
Invest R80 609 in Account A and R150 000 - R80 609,05 = R69 390,95  in Account B

OR

a = amount invested at 8,4% p.a. compounded quarterly
b = amount invested at 9,6% p.a. compounded monthly
a + b = 150 000
a = 150 000 - b

b = R69 390,95
a = R80 609,05

✓ x [1 + ^0,084/₄]⁴⁸
✓✓ (150000 - x)(1 + ^0,096/₁₂)¹⁴⁴
✓ equation
✓ R80609,05
✓ R69 390,95 (6)

OR

✓[1 + 0,096/12]144
✓✓ [150 000 - b][1 + ^0,084/₄]⁴⁸
✓ equation
✓ b
✓ a      (6)  [15]

7.1

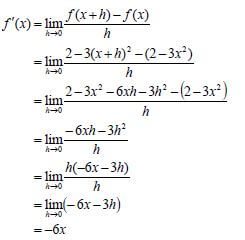✓ 2−3x² −6xh −3h²
✓ −6xh −3h²
✓ subst. into formula
✓ factorisation
✓answer                                     (5)

OR

✓ subst. into formula
✓ simplification
✓  −6xh −3h²
✓ common factor
✓  answer                                    (5)

7.2.1

D_x[4x +5)²]
= D_x(16x² + 40x + 25 )
= 32x + 40

✓ 16x² + 40x + 25
✓ 32x
✓ + 40                                        (3)

7.2.2

✓  x^¼
✓  1 - 8x^-2
✓  ¹/₄x^-¾
✓  16x^-3   (4)  [12]

8.1

C(0;12)

✓ C(0;12)                                 (1)

8.2

3

− x +13x +12 = 0

3

x    −13x −12 = 0

2

(x +1)(x − x −12)= 0

(x +1 )(x − 4)(x +3)= 0

A( − ; )

B(4;0)

✓  f (x) = 0
✓ (x +1)
✓ (x² −x−12)
✓  x = - 3 or 4
✓  clearly indicating A and B (5)

8.3

f^I (x)= −3x² +13
f^//(x)= −6x
−6x = 0
x = 0
For f(x), point of inflection will be at (0 ; 12).
For g(x), point of inflection will be at (0 ; -12).

OR

g(x) = x³ - 13x -12
g^/ (x)= 3x² −13
g^//(x)= 6x
6x = 0
x = 0
(0;−12)

OR

 f (x)= −3x² +13
TP's where
−3x² +13 = 0
x = ¹³/₃
x = ± √ ¹³/₃
= ±2,08
x-value of point of inflection: −2,08+2,08 = 0
                                                   2
For f(x), point of inflection will be at (0 ; 12).
For g(x), point of inflection will be at (0 ; -12).

✓  f^I (x)= −3x² +13
✓ f^//(x)= −6x
✓  equating to zero
✓ (0;−12)                                     (4)

OF
✓ g^/ (x)= 3x² −13
✓ g^//(x)= 6x
✓ equating to zero
✓ (0;−12)                                     (4)

OR
✓  f (x)= −3x² +13
✓  −3x² +13= 0
✓ x-values of TPs
✓ (0;−12)                                     (4)

8.4

F^Ix)= −3x² +13
−3x² +13 = −14
−3x² = −27
x² = 9
x=3 or x= −3

✓ equating derivative to - 14
✓ simplification
✓✓  answers      (4)  [14]

9.1.1

AC =  t - 30

✓ answer                                   (1)

9.1.2

30² =(t−30)² + p²                  [Pythagoras]
p² = 900 −(t −30 )²
p² = 900−(t² −60t +900)
p² = 900−t²+ 60t −900
p² = 60t −t²

✓  p² = 900 −(t −30 )^2
✓ (t² −60t +900)
✓  p² = 60t −t² (3)

9.2

V (t)= ¹/₃ π r²t
= ¹/₃ π(60t −t² )t
= 20π t² −  ¹/₃πt ³

✓ substitution   (1)

9.3

V (t)= 20π t² −  ¹/₃πt³
V (t)= 40π t −π t²
40πt −π t² = 0
t(40π −tπ)= 0
t = 0    OR   t = 40 cm
N/A

✓ 40π t
✓  −π t²
✓ answer with selection        (3)

9.4

Volume of cone
= 20(π)(40)² −  ¹/₃ π(40 )³
=10 666,67π     or   33510,33211
Volume of sphere
= ⁴/₃ πr³
= ⁴/₃ π(30 )³
= 36000π    or 113097,3355
=  10666,67π
     36000π
= 0,296296
≈ 29,63%

✓ volume of cone
✓ volume of sphere
✓  10666,67π
       36000π
✓ % cut out      (4)  [12]

10.1

10!
=3 628 800

✓ 10!
✓  answer  (2)

10.2

4!× 7!
= 120 960

OR

4!×6!×7
= 120 960

✓ 4!
✓  7!
✓ 4!× 7! or 120 960 (3)

OR

✓ 4!
✓ 6!× 7
✓ 4!×6!×7 or 120 960 (3)

10.3

 6! 
10!
=   1     or 0,000198
   5040

✓ 6!
✓ 6! or     1     or  0,000198 (2) [7]
   10!       5040

11.1

P(tennis)× P(≤35years)= P(tennis and ≤ 35years )
  21 × 80  = α
 140  140   140
a =12

✓ statement
✓ substitution
✓ answer  (3)

11.2

P(gym or ≤35 years )
= P(gym)+ P(≤ 35years)− P(gym and ≤ 35years)
=  70 + 80  − 40
   140  140 140
= 110
   140
=  11  or   0,79
   14

✓  statement
✓ ⁷⁰/₁₄₀
✓ ⁸⁰/₁₄₀
✓ ⁴⁰/₁₄₀
✓110 or 11  or  0,79   (5) [8]
   140    14