MATHEMATICS PAPER 2 QUESTIONS GRADE 12 - 2018 SEPTEMBER PREPARATORY EXAM PAPERS AND MEMOS
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 2
NATIONAL SENIOR CERTIFICATE
GRADE 12
SEPTEMBER 2018
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions in the ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTION 1
Every year the Grade 9s have to choose whether to take Mathematics or Mathematical Literacy. 15 learners were selected at random and their marks as a percentage for their Grade 9 report and their Grade 12 final exam are recorded in a table.
| Grade 9 | 27 | 40 | 53 | 55 | 65 | 67 | 68 | 76 | 79 | 79 | 80 | 83 | 88 | 94 | 94 |
| Grade 12 | 34 | 36 | 42 | 42 | 57 | 71 | 68 | 42 | 70 | 85 | 76 | 93 | 95 | 99 | 91 |
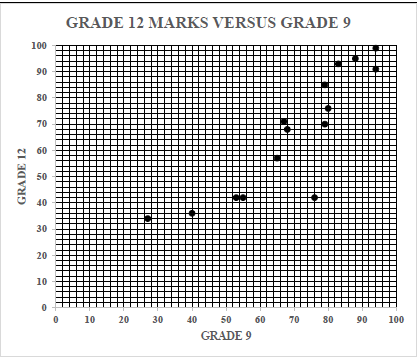
1.1 Determine the equation of the least squares regression line. (3)
1.2 If a learner in Grade 9 final exams obtains 41%, estimate what mark in percentage did he get in Grade 12. [Round off your answer to the nearest integer] (2)
1.3 Draw the least squares regression line on the scatter plot (2)
1.4 Calculate the correlation coefficient. (2)
1.5 Is the Grade 9 report mark a good predictor of the final matric mark? Motivate your answer. (2)
[11]
QUESTION 2
The number of learners absent from 11 weekend classes in a year were recorded as follows.
10 13 15 17 18 23 24 26 28 28 29
2.1 Determine the range of the above data. (1)
2.2 Calculate the average number of the learners absent from a weekend class. (2)
2.3 Calculate the standard deviation of the above data (3)
2.4 Determine the number of weeks where the attendance of the learners lies outside one standard deviation from the mean. (2)
[8]
QUESTION 3
In the diagram below, points A (p; 3), B (-3 ; -3) and C(t ; 5) are the vertices of triangle ABC. The length of BC = √89 units. The equation of line AB is y= -3x -12. E is the xintercept of line AB.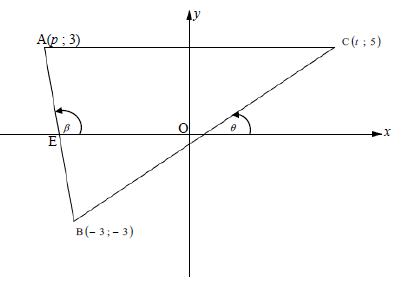
3.1 Calculate the value of t (5)
3.2 Calculate the value of p (4)
3.3 Determine the coordinates of E (2)
3.4 Determine the coordinates of M, the midpoint of AC if the value of t = 2 and p = -5. (2)
3.5 Why is EM BC ? (4)
3.6 Calculate the size of C Bˆ A (4)
[21]
QUESTION 4
In the diagram below, P(0; -3) , Q(9; -6) and R(8; -9) are the vertices of a triangle in the Cartesian plane.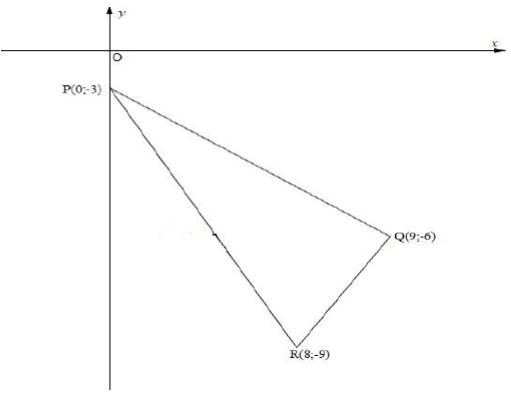
4.1 Determine the length of PR (2)
4.2 Determine the co-ordinates of the midpoint of PR (2)
4.3 Show that PQR = 90º (4)
4.4 Determine the equation of the circle passing through P, Q and R (2)
4.5 Determine the equation of the tangent to the circle P, Q and R passing through point P. (5)
4.6 T is a point with co-ordinates T (cosθ ; sinθ) , and the distance between T and R is √146 units, determine the value of tan θ . (5)
[20]
QUESTION 5
5.1 If sin A = -3/7 , where A ∈ [90º ; 270º] determine, using a diagram, without the use of a calculator, the value of sin A + 30º(4)
5.2 Simplify fully to one trigonometric ratio of x:
- sin 2(90º - x) - tan x.cos (-x) sin (-x - 360º) (6)
5.3 Show that, for any given value of A, the roots of the equation x2 - 2x sinA = cos2A are real and rational (3)
5.4 Prove the identity:
cos 3x + sin 3x = 2 (3)
sin x cos x tan 2x
5.5 If cos 22º = p and sin 38º = q, without the use of a calculator, determine the following in terms of p and q.
5.5.1 sin 68º (2)
5.5.2 cos 16º (4)
[22]
QUESTION 6
6.1 A function is defined as f ( x ) = a cos (x - p) + 1 .
The function satisfies the following conditions:
- The period is 360º
- The range is y ∈ [-1;3]
- The co-ordinates of a maximum point are [210º;3]
Write down the values of a and p. (2)
6.2 In the diagram below, the functions f ( x ) = cos (x - 60º) and g ( x ) sin 3 x are drawn for x ∈ [ -90 ;180 ]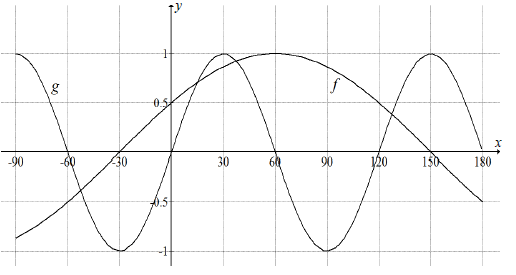 For what value(s) of x is
For what value(s) of x is
6.2.1 f ' ( x ) = 0 , where x ∈ [-90º ; 180º]? (1)
6.2.2 f ( x ) = g ( x ) , where x ∈ [- 90º ; 30º ] ? Show all relevant calculations. (6)
6.2.3 f ( x ) = g ( x ) , where x ∈ [ - 90º ; 30º ]? (2)
[11]
QUESTION 7
In the diagram below AD is a vertical structure. B, C and D are three points in the same horizontal plane. The angle of elevation of A from C is θ . BC = k metres, AB = 2BC and ABC = 2θ
7.1 Prove that AC = k√1 + 8 sin2θ (5)
7.2 Calculate the value of AC rounded off to the nearest metre, if k = 139 ,5 metres and θ = 42º (2)
[7]
Give reasons for your statements in QUESTIONS 8, 9, 10 and 11.
QUESTION 8
In the diagram below, E is the centre of the circle passing through A, B and C. AE is produced to D so that DCEB is a cyclic quadrilateral of the larger circle such that CD = EB.
CA is joined. CED = 28º
8.1 Determine the size of 2 Dˆ (2)
8.2 Give a reason why CE BD (1)
8.3 Show that CD = EC (2)
8.4 Calculate, with reasons, the size of:
8.4.1 2 B2 (4)
8.4.2 BAC (3)
[12]
QUESTION 9
In the diagram below, WXYZ is a trapezium, with XY II UV II WZ . UZ : YZ = 4 : 7 . V3 = V4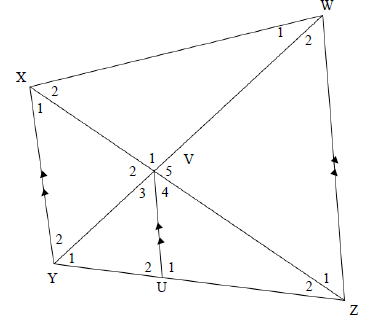
9.1 Prove that YV = XV (3)
VW VZ
9.2 Determine the numerical value of Area of Δ WVZ in a simplified form.(4)
Area of ΔXVY
9.3 Show that WXYZ is a cyclic quadrilateral. (3)
9.4 Prove that UV is a tangent to the circle passing through X, V and Y. (2)
[12]
QUESTION 10
Complete the proof of the theorem in the answer book, that states that if in ΔABC and ΔPQR, A = P, B = Q and C = R 10.1 Prove that AB = AC (6)
10.1 Prove that AB = AC (6)
PQ PR
10.2 SPQ is a common tangent for both circles. M is the centre of the bigger circle. PM is the diameter of the smaller circle. RQ ⊥ PQ . PMN = x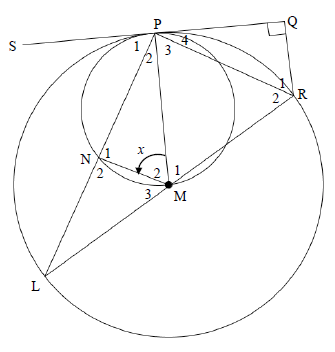
Prove that:
10.2.1 LN = NP (3)
10.2.2 PR bisects QRL (4)
10.2.3 ΔPNM ||| ΔPQR (4)
10.3 If it is given that, PR = 30 cm and QR= 15, calculate the:
10.3.1 length of LR. (5)
10.3.2 value of x (4)
[26]
TOTAL: 150
INFORMATION SHEET; MATHEMATICS