GRADE 12 MATHEMATICS PAPER 1 QUESTIONS- SENIOR CERTIFICATE EXAMINATIONS PAST PAPER MAY/JUNE2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMathematics Paper 1
Grade 12
Senior Certificate Examinations
Past Papers 2016
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will not necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 4x2 – 25 = 0 (3)
1.1.2 x2 – 5x - 2 = 0 (correct to TWO decimal places) (3)
1.1.3 (2 - x)(x+4) ≥ 0 (3)
1.1.4 x - 3x½ = (5)
1.2 Solve for x and y:
2x – y +1=0 and x2 – 3x -4- y = y2 (6)
1.3 Given: f(x) = √12x+1
1.3.1 Write down the domain of f. (1)
1.3.2 Solve for x if f(x)=2x-1. (5)
[26]
QUESTION 2
2.1 Given the arithmetic series: a + 13 + b + 27 + ...
2.1.1 Show that a=6 and b = 20 (2)
2.1.2 Calculate the sum of the first 20 terms of the series. (3)
2.1.3 Write the series in QUESTION 2.1.2 in sigma notation. (2)
2.2 Given the geometric series: (x - 2)+(x2 – 4)+(x3 + 2x2 - 4x - 8) + ...
2.2.1 Determine the values of x for which the series converges. (4)
2.2.2 If x= -3/2, calculate the sum to infinity of the given series. (3)
[14]
QUESTION 3
The first four terms of a quadratic number pattern are -1 ; 2 ; 9 ; 20.
3.1 Determine the general term of the quadratic number pattern. (4)
3.2 Calculate the value of the 48th term of the quadratic number pattern. (2)
3.3 Show that the sum of the first differences of this quadratic number pattern can be given by Sn = 2n2 +n (3)
3.4 If the sum of the first 69 first differences in QUESTION 3.3 equals 9 591 (that is, S69 = 9 591), which term of the quadratic number pattern has a value of 9 590? (2)
[11]
QUESTION 4
The sketch below shows the graphs of f(x) = -x2 – 2x+3 and g(x)= mx +q.
Graph f has x-intercepts at A and B(1 ;0) and a turning point at C.
The straight line g, passing through A and C, cuts the y-axis at E.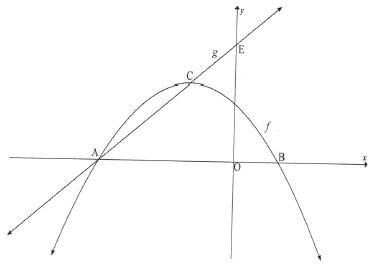
4.1 Write down the coordinates of the y-intercept of f. (1)
4.2 Show that the coordinates of Care (-1; 4). (3)
4.3 Write down the coordinates of A. (1)
4.4 Calculate the length of CE. (6)
4.5 Determine the value of k if h(x) = 2x +k is a tangent to the graph of f. (5)
4.6 Determine the equation of g-1, the inverse of g, in the form y= ... (2)
4.7 For which value(s) of x is g(x)≥ g-1(x)? (3)
[21]
QUESTION 5
The sketch below shows the graphs of f(x) = 3 + q and g(x) = 2x +r
x - p
- g intersects the vertical asymptote of f at A.
- B is the common y-intercept of f and g.
- y= 2 is the common horizontal asymptote of f and g.

5.1 Write down the value of r. (1)
5.2 Determine the value of p. (4)
5.3 Determine the coordinates of A. (3)
5.4 For which value(s) of x is f(x) - g(x) ≥ 0? (2)
5.5 If h(x) = f(x-2), write down the equation of h. (2)
[12]
QUESTION 6
6.1 How long would the price of an asset take to reduce by a third of its original value if it depreciates on a reducing balance at a rate of 4,7% p.a.? (4)
6.2 Lebogo bought a tractor for Rx on 1 April 2016.
- She will trade in this tractor when she replaces it with a similar one in 5 years time on 1 April 2021.
- The tractor depreciates by 20% p.a. according to the reducing-balance method.
- The price of a similar tractor increases by 18% annually.
- Lebogo calculated that if she deposited R8 000 per month into a sinking fund, which paid interest at 10% p.a. compounded monthly, she would have enough money to cover the replacement cost of the tractor. She made the first deposit in this fund on 30 April 2016 and will continue to do so at the end of every month until 31 March 2021.
6.2.1 Determine, in terms of x, what the book value of the current tractor will be on 1 April 2021 (that is, 5 years after it was bought). Give your answer correct to FIVE decimal places. (2)
6.2.2 Determine, in terms of x, what the price of a similar new tractor will be on 1 April 2021. Give your answer correct to FIVE decimal places. (2)
6.2.3 Calculate the amount accumulated in the sinking fund on 1 April 2021. (4)
6.2.4 Calculate the value of x, the price of the current tractor. Round off your answer to the nearest thousand. (4)
[16]
QUESTION 7
7.1 Determine f′(x) from first principles if f(x) = 3x2 - 5 (5)
7.2 Determine dy/dx if:
7.2.1 y=2x5 + 4/x3 (3)
7.2.2 y=(√x-x2)2 (4)
[12]
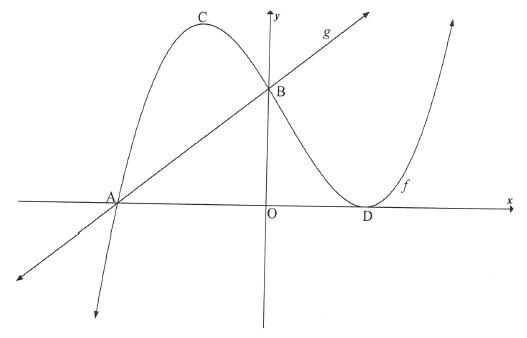
QUESTION 8
Sketched below are the graphs of f(x) = (x - 2)2(x - k) and g(x) = mx +12
- A and D are the x-intercepts of f.
- B is the common y-intercept of f and g.
- C and D are turning points of f.
- The straight line g passes through A.

8.1 Write down the y-coordinate of B. (1)
8.2 Calculate the x-coordinate of A.(3)
8.3 If k=-3, calculate the coordinates of C. (6)
8.4 For which values of x will f be concave down? (3)
[13]
QUESTION 9
A 340 ml can with height h cm and radius r сm is shown below. 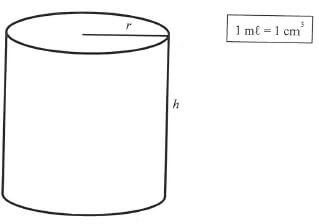
9.1 Determine the height of the can in terms of the radius r. (3)
9.2 Calculate the length of the radius of the can, in cm, if the surface area is to be a minimum. (6)
[9]
QUESTION 10
10.1 A tournament organiser conducted a survey among 150 members at a local sports club to find out whether they play tennis or not. The results are shown in the table below.
| PLAYING TENNIS | NOT PLAYING TENNIS | |
| Male | 50 | 30 |
| Female | 20 | 50 |
10.1.1 What is the probability that a member selected at random is:
(a) Female (2)
(b) Female and plays tennis (1)
10.1.2 Is playing tennis independent of gender? Motivate your answer with the necessary calculations. (3)
10.2 The probability of events A and B occurring are denoted by P(A) and P(B) respectively.
For any two events A and B it is given that:
- P(B') = 0,28
- P(B) = 3P(A)
- P(A or B) = 0,96
Are events A and B mutually exclusive? Justify your answer. (4)
[10]
QUESTION 11
Five boys and four girls go to the movies. They are all seated next to each other in the same row.
11.1 One boy and girl are a couple and want to sit next to each other at any end of the row of friends. In how many different ways can the entire group be seated? (3)
11.2 If all the friends are seated randomly, calculate the probability that all the girls are seated next to each other. (3)
[6]
TOTAL: 150