MATHEMATICAL LITERACY PAPER 1 MEMORANDUM - GRADE 12 AMENDED SENIOR CERTIFICATE EXAMINATIONS PAST PAPERS AND MEMOS MAY/JUNE 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICAL LITERACY P1
GRADE 12
MEMORANDUM
SENIOR CERTIFICATE EXAMINATIONS
2016
| Symbol | Explanation |
| M | Method |
| M/A | Method with accuracy |
| CA | Consistent accuracy |
| A | Accuracy |
| C | Conversion |
| S | Simplification |
| RT/RG | Reading from a table OR a graph |
| SF | Correct substitution in a formula |
| J | Reason/Explain/Decision |
| P | Penalty, e.g. for no units, incorrect rounding off etc. |
| R | Rounding off |
| NPR | No penalty for rounding |
QUESTION 1 [44] Tolerance range 2 marks
| Ques | Solution | Explanation | T&L |
| 1.1.1 | It is the outstanding (still owing) balance of the previous month's account. OR Opening balance for new month.✓J✓J✓J✓J | 2 J explanation (2) | L1 |
| 1.1.2 | Aug : 19 days ✓A Sep : 9 days ✓A Therefore total number of days lapsed = 19 + 9 = 28 ✓CA | 2A correct number of days per month Answer only | L1 |
| 1.1.3 | Total Basic Levy = R2 105,89 + R2 158,50 ✓MA
| 1MA adding levies Answer only full marks | L1 |
| 1.1.4 (a) | New reading – previous reading = 1 190 786 kWh – 1 158 957 kWh ✓A✓M = 31 829 kWh | 1A identify the reading 1M subtracting correct order (if dividing max 1 ) (2) | L1 |
| 1.1.4 (b) | 31 829 × 0,6303 ✓A✓M = R20 061,8187 ≈ R20 061,82 | 1A identifying the values 1M multiply by 0,6303 (2) | L1 |
| 1.1.5 | R2 105,89 + R2 158,50 + R20 061,82 + R24 781,93 ✓MA = R49 108,14 ✓A VAT =14 ×R49 108,14 ✓M 100 ≈R6 875,14 OR Amount = R6875,14 14% ✓M = R49 108,14 ✓A = R2 105,89 + R2 158,50 + R20 061,82 + R24 781,93 ✓A | 1MA adding all amounts 1A total before VAT 1M calculating 14% VAT OR 1M calculating 14% VAT 1A amount before VAT 1MA adding all amounts (3) | L2 |
| 1.1.6 | B = 24781,93 ✓MA 137 = R180,89 ✓A | 1MA dividing Answer only full marks | L1 |
| 1.1.7 | C = 2 105,89 + R2 158,50 + R20 061,82 + R24 781,93 ✓M + 6 875,14 – 0,03 = 55 983,25 ✓CA OR C = 49 108,14 + 6 875,14 – 0,03 ✓M = 55 983,25 ✓CA | 1M adding and subtracting 0,03 Answer only full marks | L2 |
| 1.1.8 | To round down the amount due to the non-availability of 1c and 2c coins. ✓✓J OR Rounding down to 5c | 2J explanation (2) | L1 |
| 1.1.9 | Monthly interest rate = 10% ÷ 12 ✓M Interest after 1 month = 1 × R55 983,25 120 ≈ R466,527 ✓A Amount payable after 1 month (November 15) = R55 983,25 + R466,527 ✓M ≈ R56 449,777 ✓CA Interest after 2 months = 1× R56 449,77 120 ≈ R470,415 Amount payable after 2 months (Dec 15) = R56 449,777 + R470,415 ≈ R56 920,19 ✓CA OR Monthly interest rate = 10% ÷ 12 ✓M Amount payable after 1 month (November 15) =  + R55 983,25 ✓M + R55 983,25 ✓M≈ R56 449,777 ✓CA Amount payable after 2 months (by 15 Dec) = ≈ R56 920, 19 ✓CA | CA from Q1.1.7 CA from Q1.1.7 | L3 |
| 1.1.10 (a) | New three-phase commercial levy = R2 105,89 + R50,00 ✓M = R2 155,89 ✓A | 1M adding R50 to a levy Answer only full marks | L1 |
| 1.1.10 (b) | New tariff per kWh = 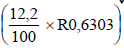 + R0,6303 ✓MA✓A + R0,6303 ✓MA✓A= 0,0768966 + R0,6303 ≈ R 0,7072 ✓CA OR New tariff per kWh = ≈ R 0,7072 ✓CA | 1MA calculating percentage of tariff Answer only full marks | L2 |
| 1.2.1 | Income is less/smaller than expenditure ✓✓J OR Expenditure is more/bigger than income ✓✓J OR Amount of shortfall from income. ✓✓J | 2J terminology used ( income & expenditure) more than /exceeds 2J less/smaller than 2J shortfall (2) | L1 |
| 1.2.2 | The municipality showed a surplus. ✓J A = R65 771 447 – R28 490 095 = R37 281 352 ✓MA | 1J decision (from the subtraction) 1MA finding differences (2) | L1 |
| 1.2.3 | Six million, nine hundred and seventy nine thousand, nine hundred and nine rand ✓✓A | 2 A correct number and wording. (If six million, five hundred and thirty thousand seven hundred and eighty five rand : Max 1 mark) (2) | L1 |
| 1.2.4 | Department B ✓✓A | 2A answer (2) | L1 |
| 1.2.5 | % difference = Expenditure2014 - Expenditure2013 ×100% Expenditure2013 = R33031602-R30645928 ×100% ✓SF R30645928 ≈ 7,784636183% ✓CA ≈ 8% ✓R | 1SF substitute correct values from table Answer only full marks | L1 |
| 1.2.6 | P = 3 ×100% ✓A✓A 7 ≈ 42,86% ✓CA | 1A numerator Answer only full marks | L2 |
| L2 |
[44]
Question 2 [28] Tolerance range 1 mark
| Ques | Solution | Explanation | T&L |
| 2.1.1 (a) | Length of rectangular area to be cleared = 1 430 mm + 250 mm × 2 ✓MA = 1 930 mm ✓CA Width of rectangular area to be cleared = 1 420 mm ✓A OR 2 marks for width and 1 mark for length | 1MA adding Answer only full marks | L1 |
| 2.1.1 (b) | Total area = 1 930 mm × 1 420 mm ✓SF = 1,93m × 1,42 m ✓C ≈ 2,7406 m² ✓CA OR Total area = 1 930 mm × 1 420 mm ✓SF = 2 740 600 mm² ✓CA ≈ 2,7406 m² ✓C OR Total area (in m2) = ( 1,73 + 0,250 × 2 ) × (0,92 + 0,25 × 2) ✓C ✓SF = 1,93 1,42 = 2,7406 ✓CA | CA from Q2.1.1 (a) | L2 |
| 2.1.2 | Length of A = 2 × 220 mm + 3 × 10 mm ✓C✓M✓MA = 470 mm | 1C converting 1M adding mortar 1MA mortar measure (Accept 450 mm) (3) | L1 |
| 2.1.3 (a) | Width of a cement slab = 2½× 22 cm + 2 cm ✓MA = 57 cm ✓CA | 1MA multiply length of one brick by 2½ and adding 2 cm (or 20mm) Answer only full marks | L1 |
| 2.1.3 (b) | Volume of one cement slab = 92 cm × 57 cm × 3,5 cm ✓C ✓SF = 18 354 cm³ ✓CA | 1SF correct values substituted from (a) Answer only full marks | L2 |
| 2.2.1 | Height = [1 800 mm – ( 2 ×40) mm] ÷ 10 ✓M ✓MA = 172 mm ✓CA | 1M subtracting 80 Answer only full marks | L2 |
| 2.2.2 (a) | Side length = √2025cm2=45cm ✓M ✓A | 1M square root Answer only full marks | L2 |
| 2.2.2 (b) | Total floor area = 2 025cm² × 15 = 30 375 cm² ✓M✓A = 3,0375 m² | 1M area multiplied by 15 Answer only full marks | L2 |
| 2.2.3 (a) | Area of circle = 3,142 × = 7,0695 cm2 | 1A 3,142 1A correct radius 1A squaring (3) | L2 |
| 2.2.3 (b) | Surface area = 180 cm × 45 cm – 10 × 7,0695 cm2 ✓SF ✓M = 8 100 cm2 – 70,695 cm2 ✓CA = 8 029,305 cm2 ✓CA | CA 45 cm from Q2.2.2(a) 1SF correct values 1M subtracting 1CA simplification 1CA total surface area (4) | L3 |
[28]
QUESTION 3 [24] Tolerance range 0 marks
| Ques | Solution | Explanation | T&L |
| 3.1.1 | ORPEN Gate ✓RD | 2RD reading from map (2) | L1 |
| 3.1.2 | R537, R536 ,R36 , R532 ✓ ✓RD | 2D reading from map (2) | L1 |
| 3.1.3 | R40 ✓ ✓RD [KZN do not mark this question.] | 2RD reading from map (2) | L1 |
| 3.1.4 | Lydenburg ✓ ✓ ✓RD | 3RD reading from map (3) | L2 |
| 3.1.5 | North West ✓ ✓RD | 2D reading from map (2) | L1 |
| 3.2.1 | Lifts ✓A ✓A Escalators ✓A Stairs/ Steps | 2A for 1st feature 1A for 2nd feature P for INCORRECT features added (3) | L1 |
| 3.2.2 | Clockwise ✓ ✓RD [Eastern Cape do not mark this question] | 2RD reading from plan (2) | L1 |
| 3.2.3 | S124 ✓A ✓A | 1A for S 1A correct number (accept 1024) (2) | L1 |
| 3.2.4 | 20 mm : 5 m ✓A = 20 mm : 5 000 mm ✓C = 20 mm : 5000 mm 20 20 = 1 mm : 250 mm Scale = 1 : 250 ✓CA | 1A ratio in different units 1C converting to the same units 1CA scale (3) | L3 |
| 3.2.5 | 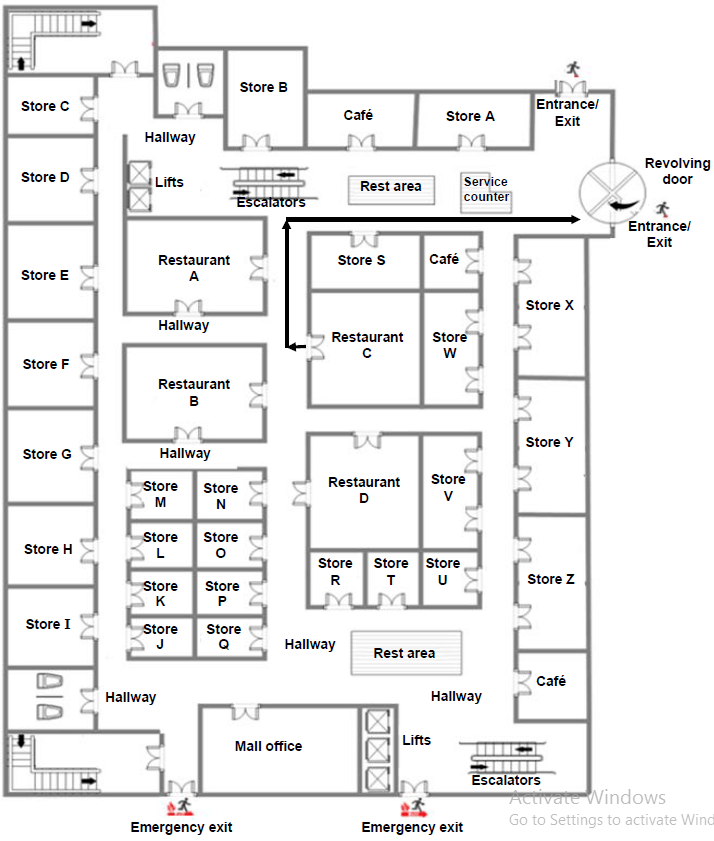 | ||
| 3.2.5 | 2A route to ANY exit 1A shortest route (3) | L2 |
Question 4 [24] Tolerance range 1 mark
| Ques | Solution | Explanation | T&L |
| 4.1 | CONTINUOUS. ✓A The data represents mass ( in kilogram) which can be expressed in smaller fractional units. ✓J | 1A continuous 1J explanation (2) | L1 |
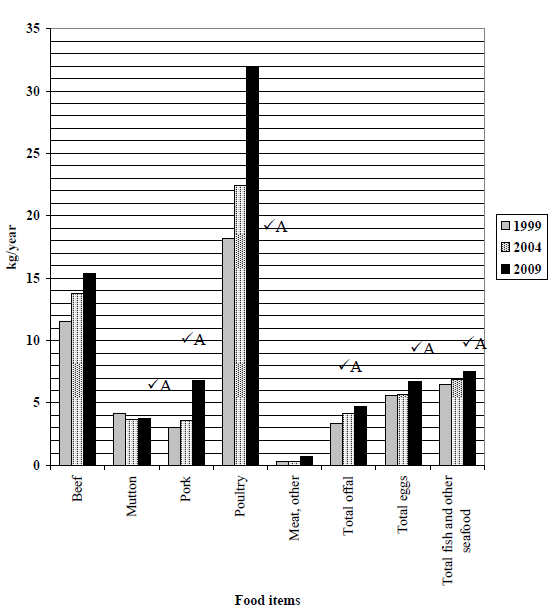
| 4.2 | Other meat ✓ ✓A 46% ✓CA | 2A item 1CA percentage (Accept Beef –7 % then Max 2 marks) (3) | L1 |
| 4.3 | 6,7 kg × 49 320 500 ✓A ✓M = 330 447 350 kg. ✓CA | 1A correct value from table Answer only full marks | L1 |
| 4.4 | M = 43,8 – (13,8 + 3,7 + 3,6 + 22,4) ✓M = 43,8 – 43,5 ✓A = 0,3 ✓CA | 1M subtracting Answer only full marks | L1 |
| 4.5 | Fish and seafood ✓ ✓A | 2A identifying fish and seafood (2) | L1 |
| 4.6 | – 46,0% ; –7,0% ; –5,0% ; 109% ; 119,0% . ✓A ✓CA ✓A | 1A Correct position Penalty 1 mark if in descending order | L1 |
| 4.7 | No mode ✓ ✓A | 2A correct answer (2) | L1 |
| 4.8 | Consumption of different food items in South Africa from 1994 to 2009
1A for each bar plotted correctly | L2 |
[24]
Question 5 [30] Tolerance range 0 marks
| Ques | Solution | Explanation | T&L |
| 5.1.1 | 5 365 : 112 043 ✓A ✓MA ≈1 : 20,884 ✓CA | 1MA writing as a ratio 1A correct values 1CA form 1:… NPR (3) | F L1 |
| 5.1.2 | R150, R200 and R300 ✓ ✓A | 2A correct values (2) | F L1 |
| 5.1.3 | % savings = 9288 × 100% ✓MA ✓M 202714 ≈4,58 % ✓CA | 1MA correct values Answer only full marks | F L1 |
| 5.1.4 | Fixed expense ✓ ✓A | 2A answer (2) | F L1 |
| 5.1.5 | R126 696 – R112 043 ✓M = R14 653 ✓CA | 1M subtract correct values Answer only full marks | F L1 |
| 5.2.1 | Charles and David Koch ✓ ✓A ✓A | 2A Charles Koch 1A David Koch (3) | DH L1 |
| 5.2.2 | $79,2 billion – $15,7 billion ✓M ✓A = $63,5 billion | 1A correct values / names 1M subtraction 1CA solution including billions (3) | DH L2 |
| 5.2.3 | 40,1 ; 40,6 ; 41,7 ; 42,9; 42,9 ; 54,3 ; 64,5; 72,7; 77,1; 79,2 ✓A Median = $ 42,9billion + 54,3billion ✓M 2 = $48,6 billion ✓CA | 1A arranging values 1M concept of median 1CA median (No penalty omitting billion) (3) | D L2 |
| 5.2.4 | Mean (in billions$) =3,9 + 6,7 + 3,3 + 7,4 + 15,7 + 4,0 + 6,3 + 6,3 + 3,1 + 4,0 ✓M 10 ✓A = 60,7 10 = 6,07 ✓CA | 1M concept of mean 1A dividing by 10 1CA simplification (No penalty omitting billion) (3) | D L2 |
| 5.2.5 | P(south african <7 ) = 2 ✓A 10 ✓A = 1 5 ✓CA | 1A numerator 1A denominator 1CA simplified fraction (3) | P L2 |
| 5.2.6 | = = R103 960 396 000 ✓CA = R 103960,3960 million ✓R ≈R103 960 million OR R103 960 000 000 OR $6,3 billion = $6 300 million $6300million ✓M 0,0606 = R 103960,3960 million ≈R103 960 million OR R103 960 000 000 | 1M dividing by rate 1CA simplification 1R rounding OR 1M dividing by rate 1CA simplification 1R rounding (3) | D L2 |
[30]