GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - SENIOR CERTIFICATE EXAMINATIONS PAST PAPERS AND MEMOS MAY/JUNE2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMathematics Paper 1
Grade 12
Senior Certificate Examinations
Past Paper (memorandum) 2016
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- Consistent accuracy applies in ALL aspects of the marking memorandum.
MEMORANDUM
QUESTION 1
| 1.1.1 | 4x2 - 25 = 0 OR 4x2 = 25 | ✓✓ factors
✓ answers (3)
✓ x2 = 25/4 ✓ x = ± √25/4 ✓ answer (3) |
| 1.1.2 | x2 - 5x - 2 = 0 OR x2 - 5x + 25/4 = 2 + 25/4 | ✔ correct substitution into correct formula
✔ answer ✔ answer (3)
✔ for adding 25/4 on both sides
✔answer ✔answer (3) |
| 1.1.3 | 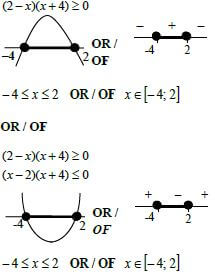 | ✔method
✔critical values in context of inequality ✔inequality or interval (3)
✔change of inequality ✔critical values in context of inequality ✔inequality or interval (3) |
| 1.1.4 | x - 3x½ - 4 = 0 OR x - 3x½ - 4 = 0 OR x - 3x½ = 4 | ✔ standard form ✔ standard form ✔ factors ✔ isolating 3√x or 3x½ ✔ factors |
| 1.2 | y = 2x +1 OR x = y - 1 | ✔ y subject of formula
✔ standard form
✔ x subject of formula |
| 1.3.1 | 2x + 1 ≥ 0 OR | ✔ answer (1)
✔ answer (1) |
| 1.3.2 | f(x) = 2x -1 √2x +1 = 2x -1 Restrictions 2x + 1 = 4x2 - 4x +1 x ≥ -½ and x ≥ ½ 4x2 - 6x = 0 x (4x -6) = 0 x = 3/2 or x = 0 ∴x = 3/2 | ✔ √2x +1 = 2x −1 ✔ standard form |
QUESTION 2
| 2.1.1 | 27 - b = b - 13 OR 27 - 13 = 2d | ✔ 27 − b = b −13
✔ 27 − 20 =13− a (2)
✔ d = 7 or 27 −13 = 2d ✔b = 13 + 7 |
| 2.1.2 | a = 6 d = 7 OR T20 = a + 19(d) | ✔ d = 7 ✔answer (3)
✔ d = 7
✔answer (3) |
| 2.1.3 | Tn= 6 + (n -1)(7) = 7n - 1 20 ∑ (6 + 7 (n -1)) n-1 20 = ∑ (7n -1) n-1 | ✔Tn= 6 + (n -1)(7) or 7n - 1 (2) |
| 2.2.1 | r = (x -2) (x + 2) x -2 or r = (x2 - 4) (x +2) x2 - 4 For convergence -1 < r < 1 -1 < x + 2 < 1 -3 < x < -1 | ✔ (x -2) (x + 2) or = (x2 - 4) (x +2)
|
| 2.2.2 | OR
| ✔a = − 7/2
✔ substitution into correct formula ✔ substitution of x = − 3/2 ✔answer (3) [14] |
QUESTION 3
| 3.1 |
OR Tn = T1 + (n -1) d1 + (n - 1)(n - 2) d2 |
✔2nd difference = 4
✔ formula ✔Tn = 2n2 - 3n (4) |
| 3.2 | Tn = 2n2 - 3n T48 = 2(48)2 - 3(48) =4464 | ✔ substitution |
| 3.3 | 3 + 7 +11.......... Sn = n/2 [2a + (n -1) d] = n/2 [2(3) + (n -1) 4] =n/2 [6 + 4n - 4] =2n2 + n | ✔ a = 3 |
| 3.4 | S69 = 9591 and T1 = -1 OR 2n2 - 3n = 9590 | ✔(9591)+ (−1) ✔ 2n2 - 3n - 9590 = 0 ✔70 (2) |
QUESTION 4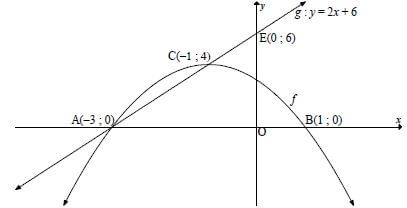
| 4.1 | (0 ; 3) | ✔ (0 ; 3) (1) |
| 4.2 | x = - b /2a or -2x -2 = 0
y = -(-1)2 -2(-1) + 3 or y = 4ac - b2 | ✔x = -2x -2 = 0 or - (-2) ✔ simplification
✔ in the context of a turning point (3) |
| 4.3 | B (1 ; 0) By symmetry A (-3 ; 0) OR x2 + 2x -3 = 0 | ✔ A(− 3 ; 0) (1)
✔ A(− 3 ; 0) (1) |
| 4.4 | Equation of g: y = 2x + q or y - 0 = 2(x + 3) E(0 ; 6) | ✔ m = 2
✔ y = 2x + 6
✔ E(0 ;6) |
| 4.5 | f'(x) = -2x -2 But mtan = 2 OR | ✔ − 2x − 2 ✔ y = 3 ✔answer (5)
✔ -x2 - 2x + 3 = 2x + k ✔ b2 - 4ac = 0 |
| 4.6 | g : y = 2x + 6 g-1 : x = 2y + 6 2y = x - 6 y = x - 6 or y = x - 3 2 2 | ✔ x = 2y + 6 ✔ y = x - 6 or y = x - 3 |
| 4.7 | g(x) ≥ g-1 (x) 2x + 6 ≥ x - 6 2 4x + 12 ≥ x - 6 3x ≥ -18 x ≥ -6 | ✔2x + 6 ≥ x - 6 |
QUESTION 5
| 5.1 | r = 2 | ✔r = 2 (1) |
| 5.2 | g(x) = 2x + 2 3 = 3 + 2 | ✔ g(0) = 2º + 2 = 3 ✔substitute B(0 ; 3) and q = 2 ✔ p = −3 (4) |
| 5.3 | at A: x = −3 y = 2-3 + 2 = 21/8 | ✔ at A : x = –3 (p-value) ✔ substitute x = –3 into exponential eqution ✔ y-value (3) |
| 5.4 | − 3 < x ≤ 0 OR (− 3; 0] | ✔ − 3 < x ✔ x ≤ 0 (2) |
| 5.5 | f (x) = 3 + 2 x + 3 f (x - 2) = 3 + 2 x - 2+ 3 h(x) = 3 + 2 x + 1 | ✔substitution of x – 2 |
QUESTION 6
| 6.1 | A= P (1 -i )n 2/3P = P( 1- 0,047)n 2/3 = (1- 0,047)n log 2/3 = nlog (1- 0,047) n = log2/3 log (1- 0,047) n = 8, 42 years | ✔A = 2/3P ✔logs |
| 6.2.1 | The book value of the tractor after 5 years book value = x(1 - 0,2)5 or x(0,8)5 =0, 32768x | ✔x(1 - 0,2)5 or x(0,8)5 ✔ 0,32768x (2) |
| 6.2.2 | Price of new tractor after 5 years book value = x(1 + 0,18)5 or x(1,18)5 =2,28776x | ✔ x(1 + 0,18)5 or x(1,18)5 ✔ 2,28776x (2) |
| 6.2.3 | 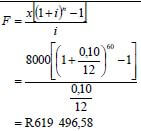 | ✔ i = 0,10/12 ✔ n = 60 ✔ subst. into future value formula ✔ answer (4) |
| 6.2.4 | Sinking fund = New tractor price – Scrap value OR 619496,58 =x(2,28776) -x(0,32768) | ✔ 619496,58
✔ R316 000 (4)
✔ 619496,58 ✔ R316 000 (4) |
QUESTION 7
| 7.1 | f(x + h) = 3(x +h)2 - 5 = 3(x2 + 2xh +h2) - 5 =3x2 + 6xh + 3h2 -5 f(x + h) - f(x) = 3x2 + 6xh + 3h2 - 5 - 3x2 +5 = 6xh + 3h2 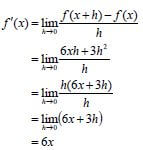 OR 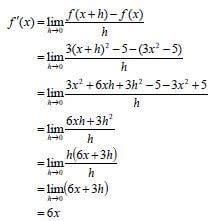 | ✔3x2 + 6xh + 3h2 - 5 ✔ f(x + h) - f(x) ✔ common factor/ (6x + 3h) ✔ answer (5)
✔ f(x + h) - f(x) ✔ 3x2 + 6xh + 3h2 - 5 ✔ 6xh + 3h2 ✔ common factor/(6x + 3h)
✔ answer (5) |
| 7.2.1 | y = 2x5 + 4/x3 y = 2x5 + 4x-3 dy /dx = 10x4 - 12x-4 | ✔ 2x5 + 4x-3 ✔ 10x4 ✔ - 12x-4 (3) |
| 7.2.2 | y = ( √x -x2)2 y = x½ - x2)2 =x - 2x 5/2 + x4 dy /dx = 1 - 5x 3/2 + 4x3 | ✔ x - 2x 5/2 + x4 |
QUESTION 8
| 8.1 | y = 12 | ✔answer (1) |
| 8.2 | 12 = (0 - 2)2(0 -k) (x - 2)2(x + 3) = 0 y = 0 | ✔ substituting (0;12) ✔ k = −3
✔ x = −3 (3)
✔–4k |
| 8.3 | f(x) = x3 + 3x2 - 4x2 - 12x + 4x +12 3x2 - 2x - 8 = 0 C[ -4/3 ; 18,52] | ✔ f(x) = x3 - x2 - 8x + 12 ✔derivative (6) |
| 8.4 | f''(x) = 6x - 2 OR f''(x) = 6x - 2 OR x = xe + xd = -4/3 + 2 | ✔ 6x − 2 ✔✔x < 1/3 (3)
✔ 6x − 2
✔✔x < 1/3 (3)
✔= -4/3 + 2 ✔✔x < 1/3 (3) |
QUESTION 9
| 9.1 | V = π r2h π r2h = 340 h = 340 π r2 | ✔formula ✔equating to 340 ✔ h = 340 |
| 9.2 | A = 2π r2 + 2π rh A'(r) = 0 for minimum surface area | ✔ 2π r2 + 2π rh |
QUESTION 10
| 10.1.1 (a) | P(Female) = 70 = 7 = 0,47 150 15 | ✔ 70 |
| 10.1.1 (b) | P(Female playing tennis) = 20 = 2 = 0,13 150 15 | ✔ answer (1) |
| 10.1.2 | P(Female) = 70 150 P(Playing) = 70 150 P(Female playing tennis) = 20 = 2 = 0,13 150 15 P(Female) × P(Playing) = 70 × 70 = 4900 = 0,22 150 150 22500 P(Female playing tennis) ≠ P(Female) × P(Playing) Therefore the event of playing tennisis not independent of gender. OR P(Male) = 80 P(Male playing tennis) ≠P(Male/Manlik) × P(Playing) OR P(Male) = 80 OR P(Female) = 70 P(Female not playing tennis) = 50 = 0,33333 | ✔P(Play ten) = 70 ✔ = 70 × 70 = 4900 = 0,22 ✔P(Female playing tennis) ≠ P(Female) × P(Playing) Not independent (3)
✔P(Playing) = 70 ✔ = 80 × 70 = 5600 = 0,25 ✔P(Male playing tennis) ≠P(Male/Manlik) × P(Playing)
✔ P(Not playing tennis) = 80
✔ P(not play ten) = 80 |
| 10.2 | P(B) = 1 - P(B') P(A or B) = P(A) + P(B) - P(A and B) | ✔ P(B) = 0,72 ✔ P(A) = 0,24 ✔ substitution into correct formula |
QUESTION 11
| 11.1 | 2 × 2! × 7! = 20 160 | ✔ 2 × 2! |
| 11.2 | All seated in 9! = 362 880 ways Girls seated together in 4! ways. P(all girls seated together) | ✔ 9! or 362 880 ✔ 4! 6! or 17280
✔ 17280 or 0,047619 21 or |
| TOTAL | 150 |