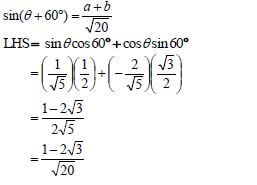MATHEMATICS PAPER 2 GRADE 12 MEMORANDUM - NSC EXAMS PAST PAPERS AND MEMOS NOVEMBER 2018
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS
PAPER 2
GRADE 12
NSC EXAMS
PAST PAPERS AND MEMOS NOVEMBER 2018
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- If a candidate has crossed out an attempt of a question and not redone the question, mark the crossed out version.
- Consistent accuracy applies in ALL aspects of the marking memorandum. Stop marking at the second calculation error.
- Assuming answers/values in order to solve a problem is NOT acceptable.
GEOMETRY | |
S | A mark for a correct statement |
R | A mark for the correct reason |
S/R | Award a mark if statement AND reason are both correct |
MEMORANDUM
QUESTION 1
1.1.1 | 140 items | ✓ answer(1) |
1.1.2 | Modal class: 20 < x ≤ 30 minutes | ✓ answer(1) |
1.1.3 | Number of minutes taken = 20 minutes | ✓answer (1) |
1.1.4 | 140 - 126 [Accept: 124 to 128]
| ✓126 |
1.1.5 | 75th percentile is at 105 items
| ✓105 |
1.1.6 | Lower quartile is at 35 items | ✓ lower quartile (Q1) |
35 | 70 | 75 | 80 | 80 |
90 | 100 | 100 | 105 | 105 |
110 | 110 | 115 | 120 | 125 |
| 1.2.1 (a) | x = 1420 15 = R94,666... = R94,67 | ✓ 1420 ✓ answer (2) | ||
1.2.1(b) | σ = R22,691...= R22,69 | ✓✓ answer (2) | ||
1.2.2(a) | They both collected the same (equal) amount in tips, i.e. R1 420 over the 15-day period. | ✓ answer (1) | ||
1.2.2(b) | Mary's standard deviation is smaller than Reggie's which suggests that there was greater variation in the amount of tips that Reggie collected each day compared to the number of tips that Mary collected each day. | ✓ explanation (1) | ||
[15] | ||||
QUESTION 2
2.1 | 251 km/h | ✓ answer (1) |
2.2.1 | r = 0,52 OR C | ✓ answer (1) |
2.2.2 | The points are fairly scattered and the least squares regression line is increasing. | ✓ reason (1) |
2.3 | There is a weak positive relation hence the height could have an influence | ✓ answer (1) |
2.4 | For (0 ; 27,07), it means that the player has a height of 0 m but can serve at a speed of 27,07 km/h. | ✓ explanation (1) |
[5] | ||
QUESTION 3
3.1.1 | mKN = y2 - y1
| ✓ correct substitution |
3.1.2 | tan θ = mKN = -3
|
|
3.2 | Inclination KL = 123,69º - 78,69º = 45º [ext ∠Δ] | ✓ S |
3.3 | y = x + c OR y - y1 = 1(x - x1) | ✓ substitute (- 1 ; 2) and m |
3.4 |
| ✓ substitute K and N into distance formula |
3.5.1 | (x + 3)2 + (y + 5)2 = 13 ...(1) OR (x+ 3)2 + (y + 5) = 13 ...(1) | ✓ equation (1) ✓ equation (1) |
3.5.2 |  | ✓ midpoint of KM |
| OR N → M N→K (x : y) → (x -4 ; y - 4) (x ; y)→(x - 2 ; y + 3) ∴L(-1 -4 ; 2-4) OR ∴L(-3 - 2 ; -5 + 3) ∴L(-5 ; -2) ∴L(-5 ; -2) | ✓ transformation ✓ x value ✓ y value | ||
3.6 |
| ✓ coordinates of T ✓ length of TL | |
[22] | |||
QUESTION 4
4.1 | F(3 ;1) | ✓ x value ✓ y value (2) |
4.2 | FS = √ (6 - 3)2 + (5 - 1)2 | ✓ substitution of F & S |
4.3 | FH(FS) : HG = 1 : 2 | ✓ HG = 10 (1) |
4.4 | Tangents from common/same point | ✓ answer (1) |
4.5.1 | FHJ = 90º [tan ⊥ radius ] | ✓ S ✓ R |
4.5.2 | (x - m)2 + (y - n)2 = 100 | ✓ answer (1) |
4.5.3 | K(22; n) [radius ⊥ tangent] OR K(22; n) [radius ⊥ tangent] | ✓ K(22; n) ✓ K(22; n) |
[18] | ||
QUESTION 5
5.1.1 | k2 = ( √5)2 - 12
| ✓ substitution into theorem of Pythagoras |
5.1.2(a) | tanθ = -½ | ✓ answer (1) |
5.1.2(b) | cos(180º + θ ) = - cosθ | ✓ reduction |
5.1.2(c) |
| ✓ expansion |
5.1.3 | tanθ = -½ | ✓ θ |
5.2 |
| ✓ single fraction ✓ single fraction ✓ double ∠ identity |
| 5.3 | 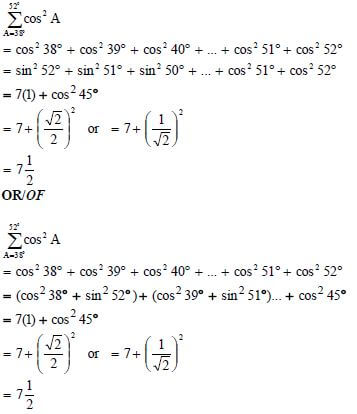 | ✓ expansion ✓ expansion |
QUESTION 6
6.1 | Period = 120° | ✓ answer (1) |
6.2 | 2 = -2tan 3/2 x OR 2 = -2 tan 3/2 x | ✓ equating |
6.3 | 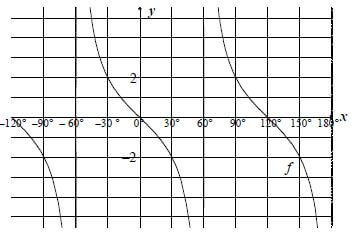 | ✓ asymptotes: x = ± 60°; x = 180° |
6.4 | x∈ (-60º ; -30º] or (60º;90º] OR –60°< x ≤ -30° or 60° < x ≤ 90° | ✓ interval ✓ interval ✓ interval ✓ interval |
6.5 |
| ✓ Translation of 40° |
[13] | ||
QUESTION 7
7.1 | ABD = 30 OR BAD = 60º | ✓ A BD = 30º ✓ BAD = 60º |
7.2 | BC2 = AB2 + AC - 2AB.ACcosBÂC | ✓ use of cosine rule in ΔABC |
[6] | ||
QUESTION 8
8.1.1 | P = M1 = 66º [tan chord theorem] | ✓S ✓R (2) |
8.1.2 | M2 = 90º [∠ in semi circle] | ✓S ✓R (2) |
8.1.3 | N1 = 180º - (90º + 66º) = 24º [sum of ∠s of ∠èΔMNP] | ✓S (1) |
8.1.4 | Ô2 = P = 66º [corres. ∠s; ∠e, PM || OR] | ✓S ✓R (2) |
8.1.5 | R + N1 + N2 = 180º - 66º = 114º [sum of ∠s of ∠e ΔRNO] OR POR = = 114º [∠s on straight line] | ✓S ✓S |
8.2
8.2.1 | FC || AB || GH [opp sides of rectangle] | ✓ R (1) |
8.2.2 | AC = AF [line || one side of Δ] OR [prop theorem; FC || GH] | ✓S ✓R |
[16] | ||
QUESTION 9
9.1
9.1 | Constr Draw KO and MO OR Constr Draw KO and MO | ✓ construction ✓ construction |
9.2
9.2.1(a) | B1 = x [∠s in same seg] | ✓ S ✓ R (2) |
9.2.1(b) | B2 = y [ext ∠ of cyclic quad] | ✓ S ✓ R (2) |
9.2.2 | C = 180º - (x + y) [sum of ∠e, Δ ACR] OR S1 = T2 [∠s in same segment] | ✓ S ✓ S |
9.2.3 | T4 = y - 30º [ext ∠ of TDR] OR AST = C + D2 [ext ∠ of SCD] | ✓ S |
[16] | ||
QUESTION 10
10.1.1 | A2 = A1 = 90º - x [= chords subtend = ∠s] OR A2 = A1 = 90º - x [= chords subtend = ∠s] OR In ∆AMC and ∆ACB: | ✓ S ✓R ✓ S ✓ R ✓ S ✓ R |
10.1.2 | In ∆ACB and ∆CMD OR In ∆ACB and ∆CMD B = D2 = x [proved OR exterior ∠ of cyclic quad.] OR In ∆ACB and/en ∆CMD | ✓ S ✓ S ✓ S |
10.2.1 | BC = AB [ΔACB ||| ΔCMD] OR C1 + C2 = B = D = x [tan chord th OR exterior ∠ of cyclic quad] | ✓ BC = AB
|
OR OR ACM = B = x [proven] | ✓ AC = AB | |
10.2.2 | In ΔDMC: OR In ΔABC: | ✓ trig ratio ✓ 2 equations for sin x |
[16] | ||
TOTAL: 150