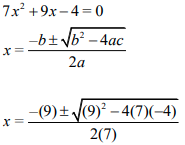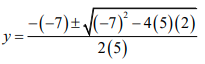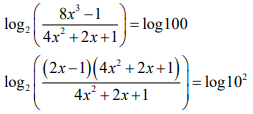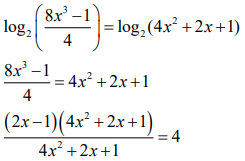TECHNICAL MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2020 PREPARATORY EXAMINATIONS

Wednesday, 15 December 2021 11:26

TECHNICAL MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2020 PREPARATORY EXAMINATIONS

More in this category: « TECHNICAL MATHEMATICS PAPER 1 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS SEPTEMBER 2020 PREPARATORY EXAMINATIONS TECHNICAL MATHEMATICS PAPER 2 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS SEPTEMBER 2020 PREPARATORY EXAMINATIONS »

Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

QUESTION 1

1.1	1.1.1	0 = (3x − 2)(x + 1) x = ²/₃ or x = −1	✓ x = ²/₃ ✓x = −1	A A	(2)
	1.1.2	7x² + 9x − 4 = 0 x = −1,64 or x = 0,35 − 1 mark for incorrect rounding	✓ Formula ✓Substitution ✓x = −1,64 ✓ x = 0,35 R	A CA CA	(4)
	1.1.3	−6x² < 5x −6x² − 5x < 0 x(6x+5) >0 Crititcal values 0 and −⁵/₆ = − 0,83 x< −⁵/₆ or 0<x	✓Factors M ✓Both critical values NPR ✓✓Correct notation for each interval	A CA CA CA	(4)
1.2	x+ 3y = 1.................(1) 2x² + 2y² = −5xy .....(2) x = 1 − 3y..................(3) 2(1−3y)² + 2y² = −5(1 − 3y)y 2(1−6y + 9y²) + 2y² = −5y + 15y² 2 −12y + 18y² + 2y² + 5y − 15y² = 0 5y² − 7y + 2 = 0 y =0,4 or y = 1 x = 1 − 3y x = 1 − 3(0,4) or x = 1 − 3(1) x = −0,2 or x = −2 OR x+ 3y = 1.................(1) 2x² + 2y² = −5xy .....(2) y = 1 − x .................(3) 3 2x² + 2( 1 − x)² = − 5x (1 − x) 3 3 2x² + 2( 1− 2x + x²) = − 5x + 5x² 9 3 18x² + 2 − 4x + 2x² = − 15x + 15x² 18x² − 15x² + 2x² − 4x + 15x + 2 = 0 5x² + 11x + 2 = 0 x = −2 or x = −0,2 y = 1− x 3 y = 1 − (−2) or y = 1 −(0,2) 3 3 y = 1 or y = 0,4		✓Equation 3 M ✓Substitution ✓Simplification ✓Standard form ✓Substitution ✓Both y values ✓Both x values NPR	A CA S S SF CA CA	(7)
1.3	1.3.1	5,425 rev/ min = 5,425 rev 60sec 5,425 rev / min = 0,09rev / sec	✓ 0,09 rev/sec	A	(1)
	1.3.2	5,425 rev / min = 9 × 10⁻² rev / sec	✓ 9 × 10⁻² rev / sec NPU	CA	(1)
1.4	101111₂ = 1 × 2⁵ + 0 × 2⁴ + 1 × 2² + 1 × 2¹ + 1 × 2⁰ = 32+ 8 + 4+ 2 + 1 = 47 AO: Full Marks		✓ Method ✓ 47	A A	(2)
					[21]

QUESTION 2

2.1

−x² + 9x − 2 = 0
b² − 4ac = 9² − 4(−1)(−2)
b² − 4ac = 73
Roots are real, irrational and unequal

✓ Substitution
✓ Δ = 73
✓ Nature of roots

SF
CA
CA

(3)

2.2

−x² + 9x − c = 0
b² − 4ac < 0
9² − 4(−1)(c) <0
4c < −81
c < −81
4

✓ Δ < 0

✓Substitution
✓⁻⁸¹/₄
✓correct notation

CA
CA
CA

(4)

[7]

QUESTION 3

3.1	3.1.1	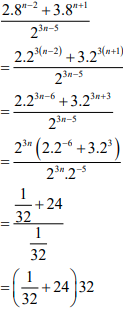= 1 + 768 = 769	✓Prime bases ✓Factorisation ✓Simplification ✓Simplification	A CA CA CA	(4)
	3.1.2	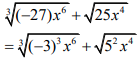= −3x² + 5x² = 2x²	✓Prime bases ✓Simplification ✓Simplification	A CA CA	(3)
	3.1.3	log₂32 ÷ 2 log ₅ 25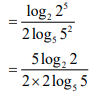 =⁵/₄	✓Prime bases ✓Log property ✓Simplification	A CA CA	(3)
3.2	Log ₂ (8x³ − 1) − log 100 = log ₂ (4x² + 2x + 1) Log ₂ (8x³ − 1) − log ₂ (4x² + 2x + 1) = log 100 log ₂ (2x − 1 ) = 2 log 10 log ₂ (2x − 1) = 2 2² = 2x − 1 x = ⁵/₂ OR Log ₂ (8x³ − 1) − log 100 = log ₂ (4x² + 2x + 1) Log ₂ (8x³ − 1) − log 10² = log ₂ (4x² + 2x + 1) Log ₂ (8x³ − 1) − 2 = log ₂ (4x² + 2x + 1) Log ₂ (8x³ − 1) − log ₂ 4 = log ₂ (4x² + 2x + 1) 2x − 1 = 4 x = ⁵/₂		✓ Log property ✓ Factors ✓log property ✓ Exponential form ✓ Simplification	A A A CA CA	(5)
3.3	z = −3 + i√3 IzI = √((−3)² + (√3)²) IzI = √12 IzI = 2√3 tan θ = ^√3/₃ θ = tan⁻¹ (^√3/₃) θ = 30° (Reference Angle) θ = 180° − 30° = 150° z = 2√3(cos 150° + i sin 150°)		✓Substitution ✓Modulus ✓tan ratio ✓Reference angle ✓Polar form	A CA A CA CA	(5)
3.4		y − i = 3xi 2 − i y − i = (3xi) (2 − i) y − i = 6xi − 3xi² y − i = 6xi − 3x(−1) y − i = 3x + 6xi y = 3x and −1 = 6x y = 3x and x − ¹/₆ y = 3(− ¹/₆) and x = − ¹/₆ y = − ½ and x = − ¹/₆ OR y − i × 2 + i = 3xi 2 − i 2 + i 2y + yi − 2i − i² = 3xi 2² − i² 2y + yi − 2i −(−1) = 3xi 4 − (−1) 2y + 1 + (y−2)i = 3xi 5 2y + 1 + (y−2)i = 15xi 2y + 1 = 0 and y − 2 = 15x y = −½ and −½ − 2 = 15x y = −½ and − ⁵/₂ ÷ 15 = x y = −½ and −¹/₆ = x	✓Conjugate product ✓i² = −1 ✓x = −¹/₆ ✓ y = −½	A CA CA CA	(4)
					[24]

QUESTION 4

4.1	4.1.1	0 = − ⁶/_x + 2 ⁶/_x = 2 x = 3	✓Equating to 0 ✓ x = 3	A A	(2)
	4.1.2	0 = x² − x − 6 0 = (x − 3) ( x + 2) x = 3 or x = −2	✓Factors ✓ x = 3 ✓ x = −2	A CA CA	(3)
	4.1.3	y = −6	✓y = −6	A	(1)
	4.1.4	x = 0 and y = 2	✓ x = 0 ✓ y = 2	A A	(2)
	4.1.5	Axis of symmetry x = −2 + 3 = ½ 2 g(½) = (½)² − ½ − 6 g(½) = ⁻²⁵/₄ Turning point (½; ⁻²⁵/₄) OR g'(x) = 2x − 1 0 = 2x − 1 x = ½ g(½) = (½)² − ½ − 6 g(½) = ⁻²⁵/₄ Turning point (½; ⁻²⁵/₄)	✓M ✓x =½ ✓y-coordinate ✓ g' (x) =0 ✓ x = ½ ✓y-coordinate	A CA CA A CA CA	(3)
	4.1.6		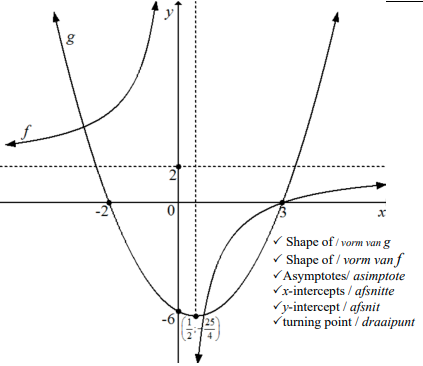CA CA CA CA CA CA	(6)
	4.1.7	x ≠ 0 OR x < 0 ∪ x > 0	✓x ≠ 0	CA	(1)
	4.1.8	x ≥ 3 OR x ∈ [3;∞]	✓ x ≥ 3	CA	(1)
4.2	4.2.1	r² = (0)² + (−2)² = 4 y = − √(4 − x²)	✓r² = 4 ✓ Equation	A CA	(2)
	4.2.2	y = 2^x + q −2 = 2⁰ + q −2 = 1 + q  q = −3	✓SF ✓q = −3	A CA	(2)
	4.2.3	y = 2^x − 3 0 = 2^x − 3 3 = 2^x x = log ₂ 3 x = 1,58 A(1,58; 0)	✓Substitution ✓Logarithm Property ✓1,58	A CA CA	(3)
	4.2.4	y > −3	✓ y > −3	A	(1)
					[27]

QUESTION 5

5.1		Depreciation value = 8,8 × 800 000 = R70 400 100 Current Asset value = R800 000 − R70 400 = R729 600 OR Current Asset value = 91,2% × R800 000 = R729 600	✓ R729 600 ✓ R729 600	A A	(1)
5.2	5.2.1	Infected people = 9	✓9	A	(1)
	5.2.2	A = P(1 + i)ⁿ 13 = 9(1 + i)⁷ T i = 0,0539 ∴ daily infection rate = 5,39%	✓Substitution ✓i ✓5,39%	SF CA CA	(3)
	5.2.3	2P = P (1 0,0339)ⁿ 2 (1,0339)ⁿ n = log_1,0339 2 ∴ n = 21 days	✓Substitution ✓Log law ✓n=21	A A CA	(3)
	5.3	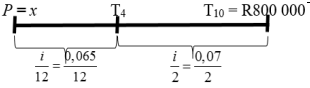A₄ = P(1 + i)ⁿ A₄ = P(1 + ⁱ/₁₂)¹²ⁿ A₄ = x(1 + ^0,065/₁₂)12×4 A = A₄(1 + ⁱ/₂)²ⁿ 800 000 = x(1 + 0,065)^12×4 (1 + 0,07)^2×6 12 2 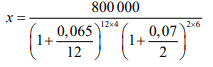∴ x = R 408 501,77	✓ Substitute SF ✓Substitute i and n SF ✓Substitution SF ✓Simplification S ✓R 408 501,77	A A CA CA CA	(5)
					[13]

QUESTION 6

6.1	ƒ(x) = −½x + π ƒ' (x) = lim_h→0 ƒ(x + h) −ƒ(x) h ƒ' (x) = lim_h→0 −½(x + h) + π −(−½x + π) h ƒ' (x) = lim_h→0 −½x −½h + π + ½x −π h ƒ' (x) = lim_h→0 −½h h ƒ' (x) = lim_h→0 −½ ∴ ƒ' (x) = −½		✓Definition ✓Substitution SF ✓Simplification S ✓Simplification S ƒ' (x) = −½	A A CA CA CA	(5)
6.2	6.2.1	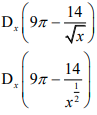D_x (9π − 14x^−½)	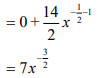✓Simplification S ✓Simplification S ✓Derivative	A A CA	(3)
	6.2.2	2xy + x = x⁻⁹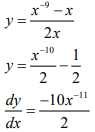 ∴ ^dy/_dx = −5x⁻¹¹	✓y Subject ✓✓Simplification S ✓−5x⁻¹¹	A CA CA CA	(4)
6.3		= −3 = 1 −2−x₁ −3 = −2 −x₁ ∴ x₁ = 1 or Avarage gradient = −3 = 1 x₁ + 2 −3 = x₁ + 2 ∴ x₁ = −5	✓Definition ✓Substitution ✓1 ✓−5	A A CA CA	(4)
					[16]

QUESTION 7

7.1	y=2	✓	A	(1)
7.2	h(½) = 2(½)³ + (½)² − 5(½) + 2 = 0 Since h(½) = 0, then x = ½ is the x -intercept	✓h(½) = 0 ✓x = ½	A A	(2)
7.3	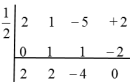(2x² + 2x − 4) ( x− ½) = 0 (2x − 2)(x+2)(x − ½) = 0 x = −2 or x = 1	✓ 2x² + 2x − 4 ✓(x + 2) (2x − 2) ✓ x = −2 or x = 1	A CA CA	(3)
7.4	h'(x) = 6x² + 2x − 5 = 0 x = −2±√(4 − 4 (6)(−5)) 12 x = −1,09 or x = 0,76 y = 2(−1,09)³ +(−1,09)² −5 (−1,09) + 2 = 6,05 or y = 2(0,76)³ + (0,76)² −5(0,76) + 2 = −0,34 (−1,09; 6,05) and (0,76; −0,34)	✓h' (x) = 6x² + 2x −5 ✓h' (x) =0 ✓Substitution ✓Both x values ✓Both y values	A A CA CA CA	(5)
7.5		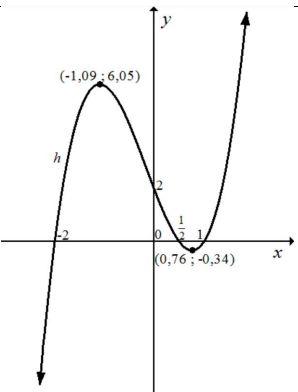✓Shape ✓x-intercepts ✓y-intercepts ✓Turning points	A CA CA CA	95)
7.6	h'(x) = 6x² + 2x − 5 = m_tangent m_tangent = − 5 y −y₁ = m(x − x₁) y − 2 = −5(x −0) y = −5x + 2	✓ m_tangent = h'(x) = 6x² + 2x − 5 = ✓ m_tangent = − 5 at x = 0 ✓Substitution SF ✓y = −5x + 2	A A CA CA	(4)
				[20]

QUESTION 8

8.1	S(t) = 3 + 6t −¾t²AO: FULL MARKS Truck weight = S(0) = 3 + 6(0) −¾(0)² =3m	✓ 3m	A	(1)
8.2	S(t) = 3 + 6t −¾t²AO: FULL MARKS S(2) = 3 + 6(2) −¾(2)² S(2) = 12m	✓Substitution ✓12m	A CA	(2)
8.3	S(t) = 3 + 6t −¾t² S'(t) = 6 − ³/₂ t 6 − ³/₂t = 0 t = 4s	✓S'(t) ✓S'(t) = 0 ✓ 4s	A A CA	(3)
8.4	Maximum Height = S(4) = 3 + 6(4) −¾(4) = 15 No, maximum height that can be reached is 15m. OR 3 + 6t −¾t² = 16 −13 + 6t −¾t² = 0 t = Non-real This indicates that it is not possible for the height of water ejected by the fire truck to reach 16m, and so this truck is not suitable.	✓Substitution ✓15m ✓Conclusion ✓Reason ✓Equating to 16 ✓Non-real ✓Conclusion ✓Reason	A A CA CA A A CA CA	(4)

QUESTION 9

9.1	9.1.1.		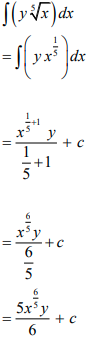✓ Exponential form S ✓c ✓	A A CA	(3)
	9.1.2	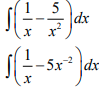In x + 5x⁻¹ + c	✓Fraction S ✓In x ✓5x⁻¹ + c	A A CA	(3)
9.2	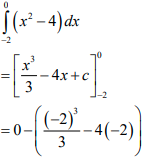= − ( −⁸/₃ + 8) ∴ Area = ¹⁶/₃ ≈ 5,33		✓Area notation ✓Integral/ ✓Substitution ✓ Substitution ✓Simplification ✓ Correct value of the bounded area	A A CA CA CA CA	(6)
					[12]
	TOTAL				150

Last modified on Friday, 18 February 2022 07:25

Published in Grade 12 September 2020 Preparatory Examinations

TECHNICAL MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2020 PREPARATORY EXAMINATIONS

Related items