NATIONAL SENIOR CERTIFICATE
GRADE 12
SEPTEMBER 2020
TECHNICAL MATHEMATICS P2

INSTRUCTIONS AND INFORMATION

Read the following instructions carefully before answering the questions.

1. This question paper consists of 11 questions.
2. Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
3. Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining the answers.
4. Answers only will NOT necessarily be awarded full marks.
5. You may use an approved scientific calculator (non-programmable and non-graphical) unless stated otherwise.
6.  If necessary, round off your answers to TWO decimal places, unless stated otherwise.
7. Diagrams are NOT necessarily drawn to scale.
8. An information sheet with formulae is included at the end of the question paper.
9. Write neatly and legibly.

QUESTION 1

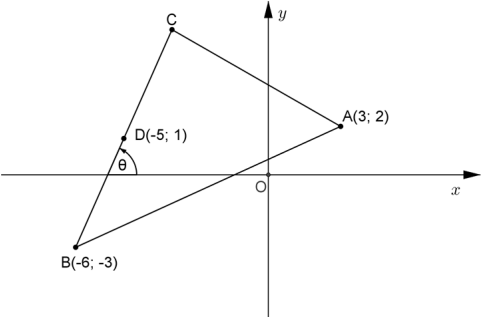
In the diagram below A(3; 2), B(−6; −3) and C are the vertices of ΔABC. D (−5;1) is the midpoint of BC.
Straight line BC makes an angle θ with the x-axis.

1.1 Calculate the length of AB. (2)
1.2 Determine:
1.2.1 The gradient of BC (2)
1.2.2 The size of θ, rounded off to ONE decimal digit (2)
1.2.3 The coordinates of C (4)
1.2.4 The equation of the line parallel to BC that goes through the point A in the form y = … (3)
[13]

QUESTION 2

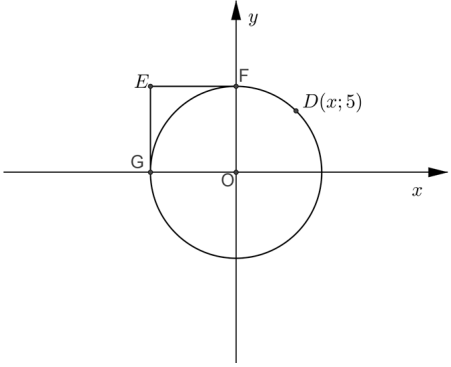
2.1 In the diagram below, the equation of the circle is given by x² + y² = 49. The point D (x;5) is a point on the circumference of the circle. EF and EG are tangents to the circle drawn from a common point, E, outside the circle.

2.1.1 Determine the x-coordinate of D. Leave your answer in simplified surd form. (3)
2.1.2

1. Write down the equations of EF and EG. (4)
2. Hence, write down the coordinates of E. (1)

2.2 The equation of an ellipse is given by 16x² + 49y² = 784 
2.2.1 Rewrite the given equation into standard form. (2)
2.2.2 Hence, sketch the graph of the equation, clearly indicating the intercepts and the shape. (3)
[13]

QUESTION 3

3.1 If Â=123° and B̂ =  65°, calculate the values of the following (rounded off to TWO decimal digits):
3.1.1 cosec A − tan B (2)
3.1.2 cot² (A + 2B)   (2)
3.2 Calculate: sin ^π/₆ + sec^2 π/₄       (3)
3.3 If 12 cosec θ = 13  and θ ∈ [90° ;270° ], with the aid of a sketch, calculate the value of cot θ − sec θ      (5)
3.4 Use fundamental identities and NOT a sketch to simply the following:
  ( tan²θ + 1) (1 − cos²θ)       (4)
3.5 Simplify to a single trigonometric ratio of x:
    sin (180° + x).tan135°                      (6)
sec(180° − x) .cos (360° − x)
[22]

QUESTION 4

Given ƒ(x) = sin 3x and g(x) =  − cos x for x ∈ [0° ;180° ]

4.1 Use the set of axes provided in the SPECIAL ANSWERBOOK to draw sketch graphs of the curves of ƒ and g for x ∈ [0°;180° ]. Clearly show ALL intercepts with the axes, coordinates of all turning points and end points of both curves. (5)
4.2 Use the graphs drawn in QUESTION 4.1, or otherwise, to determine the following:
4.2.1 The period of ƒ         (1)
4.2.2 The value(s) of x ∈ [0° ;180° ] for which:

1. g(x) ≥ 0       (2)
2. ƒ (x). g(x) ≤ 0       (4)
3. ƒ(x) − g(x) = −1     (2)

[14]

QUESTION 5

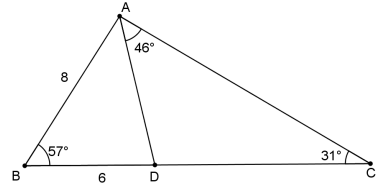
In the diagram below ABC is given with AB = 8 units, BD = 6 units.

• B̂ = 57°
• Ĉ = 31°
• CÂD 46°

Calculate the following:
5.1 The area of ΔABD (3)
5.2 The length of AD (4)
5.3 The length of CD (4)
[11]

QUESTION 6

6.1 Complete the following statement:
The line segment joining the centre of the circle with the midpoint of a chord … (1)
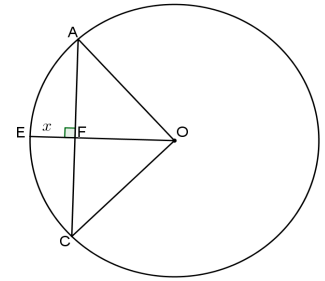
6.2 In the diagram below, O is the centre of circle AEC.

• OFE ⊥ AFC
• AC = 48 units
• OF = 7 units
• EF = x units

6.2.1 Write AO in terms of x. (1)
6.2.2 Calculate, with reasons, the value of x. (5)
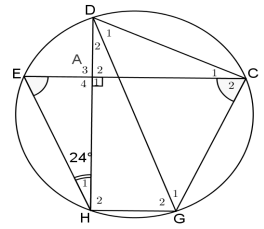
6.3 In the diagram below, DG is a chord of the circle DEHGC.

• DAH ⊥ EAC 
• Ĥ₁ = 24°
• Ê = Ĉ₂ 

6.3.1 Name THREE angles each equal to 66°, stating reasons. (4)
6.3.2 Determine the size of HĜC      (2)
6.3.3 Prove that DG is a diameter of the circle. (3)
[16]

QUESTION 7

7.1 Complete the following statement:
If a line is drawn through the endpoint of a chord making an angle with the chord equal to an angle in the alternate segment, then the line …      (1)
7.2 In the diagram below, O is the centre of the circle DFHE.

• DE is a diameter to the circle.
• GF is a tangent to the circle at F.
• D₁ = 16°
• F₁ = 37°

ˆ
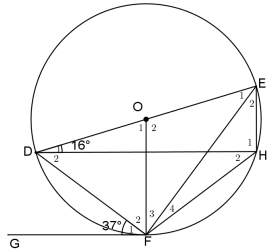
Determine, with reasons, the size of the following:
7.2.1   H₂     (2)
7.2.2   F₂      (2)
7.2.3   O₂     (2)
7.2.4   E₂      (3)
[10]

QUESTION 8

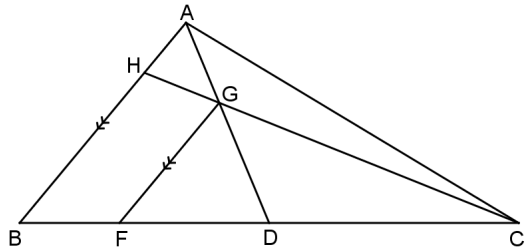
8.1 Complete the following statement:
If a line is drawn … to one side of a triangle, then the line divides the other two sides proportionally. (1)
8.2 In the diagram below, ABC is a triangle with D the midpoint of BC.

• H is a point on AB such that AD and HC intersect at G.
• AB ∥ FG with F on BC
• AG : AD = 1 : 3

Determine, with reasons, the numerical value of:
8.2.1  BF     (3)
          FD
8.2.2    CG   (3)
            CH
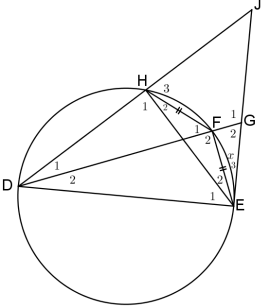
8.3 In the diagram below, DE is the diameter of circle DHFE and HF = FE.

• JE is a tangent to the circle at E.
• DHJ is a straight line.
• DF produced meets tangent EJ at G.
• Ê₃ = x

8.3.1 Write down, with reasons, THREE other angles that are each equal to x. (5)
8.3.2 Prove that: ∆DFE /// ∆DEG    (6)
[18]

QUESTION 9

In the diagram below, O is the centre of the circle with CÔD = 60° and OD = 5 cm.

9.1 Determine the arc length CD in cm. (4)
9.2 Determine the area of the sector. Leave the answer in radians and to the nearest integer. (4)
9.3

1. Determine the length of the chord CD. (2)
2. Hence, determine the height of the segment between the chord CD and the arc CD. (5)
   [15]

QUESTION 10

10.1 A petrol lawn mower has a pull chord to enable the engine to start. In order for the engine to start, the pulley must turn at 180 rpm. The pulley has a radius of 6 cm.
10.1.1 How many radians per second must the pulley turn? (2)
10.1.2 How fast must the chord be pulled to start the mower? (3)
10.1.3 Hence, determine the angular velocity of the pulley. (3)
10.2 A right cylindrical container holds exactly one litre of water. What should the height of the container be if the radius is 12 cm?
V = Lbh      V = πr²h        V = ⁴/₃ πr³        (4)
[12]

QUESTION 11

The area of an irregular metal sheet, with one side a straight side, is 256m². The ordinates are 2,2 m; 2,8 m; 3,1 m; 3,2 m; 2,9 m; 2,6 m; 2,1 m.
Calculate:
11.1 The constant interval between the ordinates (4)
11.2 The length of the straight side (2)
[6]
TOTAL: 150

INFORMATION SHEET