Technical Mathematics P2 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations

More in this category: « Technical Mathematics P1 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations Technical Mathematics P1 Grade 12 Errata - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations »

Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

MARKING CODES
M	Method
MA	Method with accuracy
A	Accuracy
CA	Consistent accuracy
S	Simplification or Statement
R	Reason
SR	Statement and correct reason
SF	Substitution correctly in correct formula

MARKING SCHEME

QUESTION 1

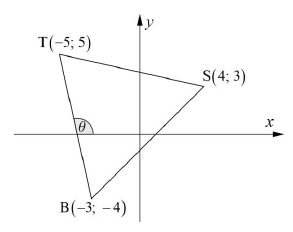1.1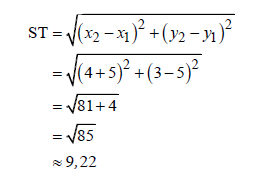

√ SF
√ S
√ Length as a decimal

(3)

1.2

mBT = y2 - y1
x2 - x1
= 5 + 4
- 5 + 3
= - 9
2

√ SF
√ S

(2)

1.3

tan θ = mBT
= - 9
2
θ = 180º - tan^-1(⁹/₂)
=180º - 77,47º
= 102,5º

√ SF
√ S 180º -
√ S 77,47º
√ Value of θ

(4)

1.4

y - y1 = m(x - x₁)
y - 3 = -9 (x - 4)
2
y = - 9x + 21
2

√ gradient
√ SF CA
√ equation

(3)

[12]

QUESTION 2

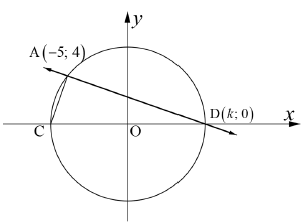2.1

x² + y² = (-5)² + 4²
= 25 + 16
= 41

√ SF A
√ equation

(2)

2.2

x² + 0² = 41
x = ± √41
∴k = √41

√ S A
√ S CA
√value of K

2.3

mOA = 4
-5

√ S

2.4

m_tangent = ⁵/₄
∴ equation of tangent
y - y1 = m(x - x1)
y - 4 = ⁵/₄(x + 5)
y = ⁵/₄x + ⁴¹/₄

√ gradient CA
√ SF CA
√ equation

2.5

mAD × mCA = 4 - 0 × 4 - 0
-5 - √41 -5 + √41
= 16
25 - 41
= 16
-16
= -1
∴AD ⊥ CA (prod of grad = -1)
OR
AD² = ( -5 - √41 )² + (4 - 0)²
=25 + 10√41 + 41 + 16
= 82 + 10√41
C(-√41;0)
AC² = (-5 + √41)² + (4 - 0)²
= 25 - 10√41 + 41 + 16
= 82 - 10√41
AD² + AC² = 82 + 10√41 +82 - 10√41
= 164
CD = CO + OD
= √41 + √41
= 2√41
CD² = 4 × 41
= 164
∴ AD² + AC² = CD²
∴ DAC = 90º (converse of pythagoras)
No marks for angle in semicircle

√ gradients CA
√ SF CA
√ S CA
√ R
√ AD² & AC²CA
√ AD² + AC²CA
√ CD² CA
√ R

(4)

[13]

QUESTION 3

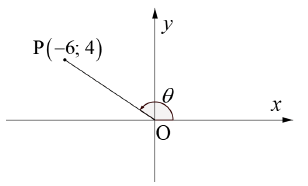3.1.1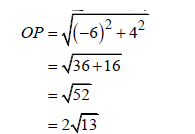

√ applying pythagoras M
√ value of OP

(2)

3.1.2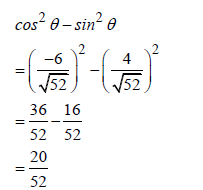

√ value of cos θ CA
√ value of sin θ CA
√ SF A
√ S CA

(4)

3.1.3

cot θ - 2
= 4 - 2
-6
= - 8
3

√ value of cot θ CA
√ S CA

(2)

3.2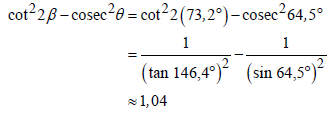

√ SF A
√ S 146,4º A
√ 1 M
tan 146,4º
√ 1 M
sin 64,5º
√√ value CA

(6)

3.3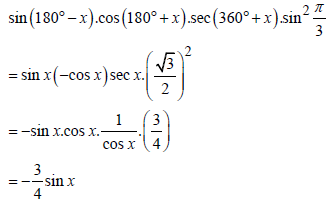

√ sin x A
√ -cos x A
√ sec x A
√ √3 A
2
√ I 1 A
cos x
√ ¾ C A
√ -¾ sin x CA

(7)

3.4.1

4cos(2θ + 20º) = 2,178
cos(2θ + 20º) = 0,5445
2θ + 20º = 57º
θ = 18,50º

√ S A
√ S only 1st quadrant CA
√ value of θ CA

3.4.2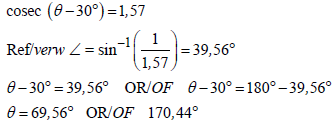

√√ ref ∠ A
√ 1st quad A
√ 2nd quad A
√ value quad 1
√ value quad 2

QUESTION 4

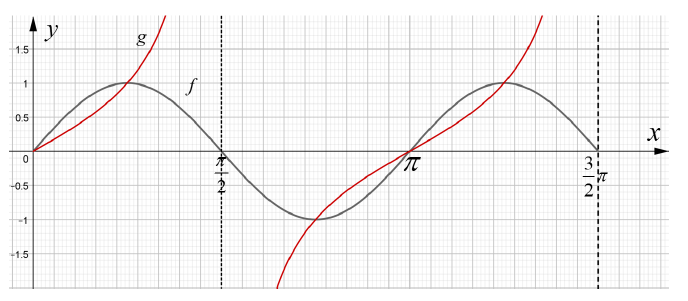4.1.1.

A: x = π = 90º
2

√ S A

(1)

4.1.2

P = 2

√ S A

(1)

4.1.3

Y = -1

√ S A

(1)

4.2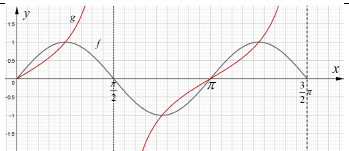

√ Shape A (intercept at the turning points of f)
√ x-intercept A
√ asymptotes CA

(3)

4.3.1

x∈{180º;225º}
OR
x∈{π; 5π}
4

√ x= 180º = π CA
√ x = 225º = 5π CA
4

(2)

4.3.2

x∈[0º;45º] = [0;π]
4
AND
x∈(90º;135º) = (π ; 3π)
2 4

√ critical values CA
√ notation CA
√ critical values CA
√ notation CA

(4)

[12]

QUESTION 5

CA = tan 35º
AB
CA = AB tan 35º
In Δ ABD;
D = 86,5º (Int ∠s of Δ)
AB = AD
sin86,5 sin40,61
AB = 6sin86,5
sin40,61
≈ 9,2 m
OR
AB² = AD² + BD² - 2AD.BDcos86,5
=6² + 7,35² - 2(6)(7,35)cos86,5
= 84,638...
AB≈9,2m
∴CA = 9,2tan35º
≈ 6,4 m

√ S
√ S
√ SR
√ S
√ SF
√ S CA
OR
√ S
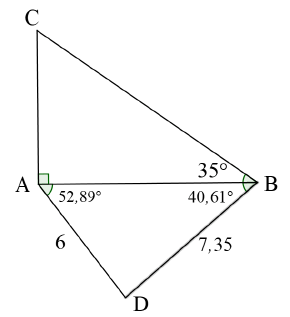√ SF
√ S CA
√ S
√ S CA

(6)

[6]

QUESTION 6

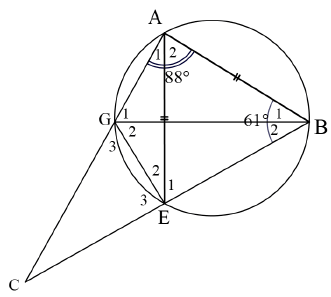6.1

E₁ = 60º (∠s opp = sides)
G₁ = 61º (∠s in same seg)
G₃ = 61º (ext ∠ of cyclic quad)

√ SR
√S√R
√S√R

(5)

6.2.1

E₂ = 180º - 88º - 61º (opp ∠s of cyclic quad)
= 31º

√S√R

(2)

6.2.2

B₁ = 31º (∠s in same segm)
∴ B₂ = 30º

√S√R
√S

(3)

[10]

QUESTION 7

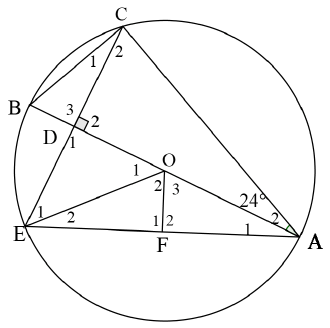7.1

C = 90º (∠in semi circle)
B = 66º (int ∠s of Δ)

√ SR
√S√R

(3)

7.2.1

in ΔADC and ΔADE
AD is common
(line frm center ⊥ to chord)
D₁ = 90º = D₂
∴ΔADC = ΔADE (SAS)

√S
√SR
√ S
√ R

(4)

7.2.2

A₁ = A₂ (Ξ Δs)
∴ DA bisect

√ S

(1)

7.2.3

O1 = 48º (∠ at centre = 2 × ∠ at circumf)

√S√R

(2)

7.3

F₂ = 90º
(line from centre to midpoint of chord)
∴ DOFE is cyclic (converse ext ∠ of cyclic quad)

√S√R
√R

(3)

[13]

QUESTION 8

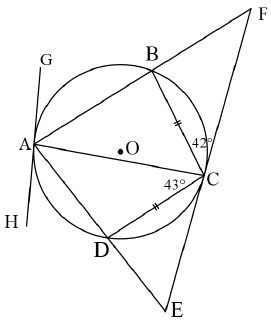8.1.1

BAC = 42º
(tan-chord)
DAC = 42º
(equal chords; equal ∠s)

√S√R
√S√R

(4)

8.1.2

ADC = 95º (int ∠s of Δ)
ABC = 85º (opp ∠s of cyclic quad)
F = 43º (ext ∠ of Δ)

√S√R
√S√R
√S√R

(4)

8.2

HAD = 43º (tan-chord)
F = 43º
(proved in 8.1.2)
GAH a tangent to AFE (converse tan-chord th)

√S√R
√R

(3)

[11]

QUESTION 9

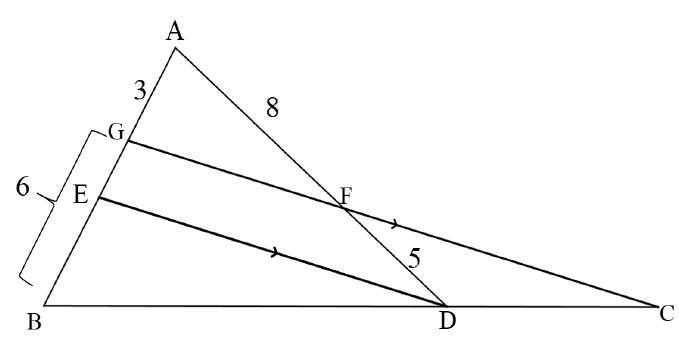9.1

let GE = x
GE = FD (prop th; ED II GF)
x = 5
3 8
x = 15
8
x = 1,875
x ≈ 2

√S√R
√S (ratio)
√S (value of x)
√S (rounding)

(5)

9.2

In Δ GBC
BC = BG (prop th; GC II ED)
BD BE
= 6
4
= 3
2

√S√R
√S CA
(value of BE)
√S value

(3)

[8]

QUESTION 10

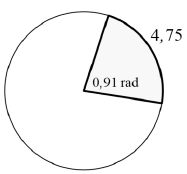10.1.1

s = rθ
r = s
θ
= 4,75
0,91
= 5,22 cm

√ formula
√ r subject
√ SF A
√ S CA

(4)

10.1.2

circumference = 2πr
= 2π(5,22)
≈ 32, 80 cm

√ formula A
√ SF A
√ S CA

(3)

10.2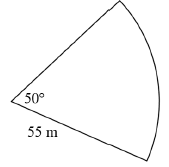

10.2.1

50º = 50º × π ≈ 0,873 rad
180º

√ M
√ A
√ rounding

(3)

10.2.2

floodlit area = area of sector
= ½ r²θ
= ½ (55)²(0,873)
≈ 1320m²

√formula
√ SF
√ S CA

(3)

10.3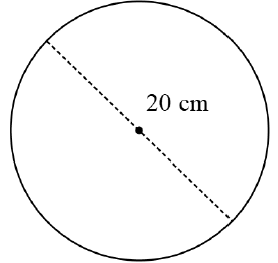

10.3.1

r = 20 = 10 cm
2

√ A

(1)

10.3.2

n = 215 rev
ϖ = 2πn
= 2π (215)
= 430 π rad

√ formula A
√ SF A
√ value of ϖ CA

(3)

10.3.3

V = ϖr
= 430π × 10
= 4300π cm/min

√ formula
√ SF A
√ value of v CA

(3)

10.3.4

4300π cm/min = 4300πcm × 60 min × 1 km
1 min 1 hr 10 000cm
= 25,8 π
≈ 81 km/h

√ M × 60
√ M × 1
10 000
√ S CA
√ rounding CA

(4)

[24]

QUESTION 11

time t(s)	0	1	2	3	4	5	6
speed v (m/s)	0	2,5	5,5	8.75	12,5	17,5	24

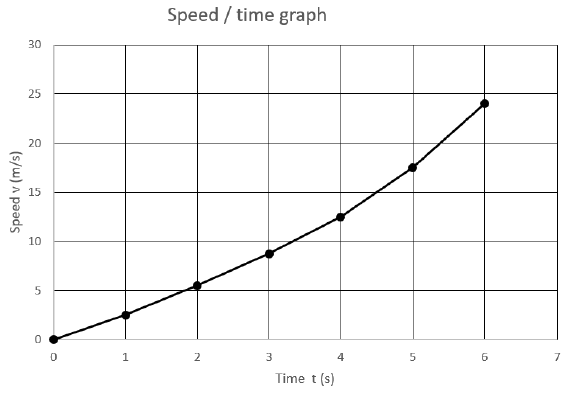11.1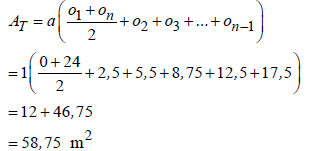

√ formula A
√ value of a A
√ SF A
√ value of A_T CA

(4)

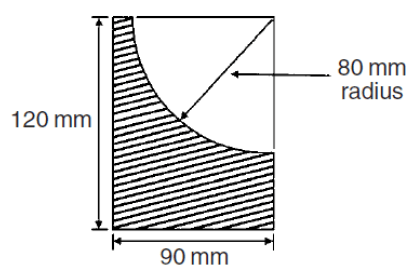11.2

Area of full rectangle = 1 × b
= 120 × 90
= 10800 mm²

Area of quater circle = ¹/₄πr²
= ¹/₄π(80)²
= 1600π

Area of figure = 10800 - 1600π
= 5773,45 mm²

✓formula
✓SF A
✓ value of rectangle
✓formula
✓SF A
✓ value of circle
✓ value of figure

(7)

[11]

TOTAL

150

Last modified on Thursday, 10 February 2022 13:46

Published in Grade 12 September 2019 Preparatory Examinations

Technical Mathematics P2 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations

MARKING SCHEME

Related items