PHYSICAL SCIENCES PAPER 1 GRADE 12 MEMORANDUM - NSC EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupPHYSICAL SCIENCES PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE EXAMINATIONS
MEMORANDUM
MAY/JUNE 2021
QUESTION 1
1.1 B ✓✓(2)
1.2 D ✓✓(2)
1.3 C ✓✓ (2)
1.4 C ✓✓ (2)
1.5 C ✓✓ (2)
1.6 A ✓✓ (2)
1.7 A ✓✓(2)
1.8 D ✓✓ (2)
1.9 A ✓✓ (2)
1.10 B ✓✓(2)
[20]
QUESTION 2
2.1 Marking criteria
If any of the underlined key words/phrases in the correct context are omitted: - 1 mark per word/phrase.
The perpendicular force exerted by a surface on an object in contact with the surface. (2)
2.2 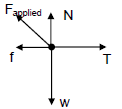
| Accepted symbols | |
| N | FN/Normal/Normal force/173,5N |
| f | Ff /fk /frictional force/kinetic frictional force/5N |
| w | Fg /mg/Weight/FEarth on block/Fw/Gravitational force/196N |
| T | Tension/FT |
| Fapplied | F/Applied force/35 N/ FA |
Notes
- Mark is awarded for label and arrow.
- Do not penalise for length of arrows
- Deduct 1 mark for any additional force
- If all forces are correctly drawn and labelled, but no arrows, deduct 1 mark.(5)
2.3 For the 20 kg:
Fnet = ma
T – f – FAx = ma
T – 5 – 35 cos40° = 0
T = 31,81 N
For m:
Fnet = ma
mg – T = ma
m(9,8) – 31,81 = 0
m = 3,25 kg
Marking criteria
- Formula for 20 kg or m kg = ma
- Substitution of zero into either formula
- All substitutions into Fnet for 20 kg as shown
- Substitution of value of T in eqn for m
- Final answer: 3,25 kg (5)
2.4.1 Decreases (1)
2.4.2 POSITIVE MARKING FROM QUESTION 2.3
Moving to the right
Velocity decreases
Accelerates/Net force to left
OR
As the tension force decreases, the net force/acceleration acts in the opposite direction of motion /to the left.
Moving to the left
Velocity increases
Accelerates/Net force to left(3)
[16]
QUESTION 3
3.1 (Motion of an object) under the influence of gravity (weight) only. (2 or 0)
OR
(Motion in which) the only force acting on the object is gravity (weight). (2)
3.2.1 Δt = 0,67 – 0,64 = 0,03 s (2)
3.2.2
OPTION 1
Δt =(1,90-0,67)
2
= 0,62 s (0,615 s)
OPTION 2
Δx = viΔt + ½ aΔt2
(-1,85) = 0 + ½ (-9,8)Δt2
Δt = 0,61 s (0,6145 s) (2)
OPTION 3
Δt =(1,90 - 0,67)
2
= 1,285 s
Δt = 1,285 – 0,67
= 0,62 s (0,615 s)
OPTION 4
vf2 = vi2 + 2aΔx
0 = vi2 + 2(-9,8)(1,85)
vi = 6,02 m·s-1
vf = vi + aΔt
0 = 6,02 + (-9,8)Δt
Δt = 0,61 s
3.2.3 POSITIVE MARKING FROM QUESTION 3.2.2
Marking Criteria
- Any appropriate formula
- Correct substitution
- Final answer: 5,94 to 6,08 m·s-1
OPTION 1
Upwards positive
vf = vi + aΔt
0 = vi + (-9,8)(0,62)
vi = 6,08 m·s-1 (6,076 m·s-1)
Downwards positive
vf = vi + aΔt
0 = vi + (9,8)(0,62)
vi = -6,08
6,08 m·s-1 (6,076 m·s-1)
OPTION 2
Upwards positive
Δy = viΔt + ½ aΔt2
1,85 = vi (0,62) + ½ (-9,8) (0,62)2
vi = 6,02 m·s-1 (6,022 m·s-1)
Downwards positive
Δy = viΔt + ½ aΔt2
1,85 = vi (0,62) + ½ (9,8) (0,62)2
vi = -6,02
vi = 6,02 m·s-1 (6,022 m·s-1)
OPTION 3
Motion from top to bottom
Downwards positive
vf2 = vi2 + 2aΔy
vf2 = 0 + 2(9,8)(1,85)
vf = 6,02 m·s-1
initial velocity =6,02 m·s-1
Upwards positive
vf2 = vi2 + 2aΔy
vf2 = 0 + 2(-9,8)(-1,85)
vf = 6,02 m·s-1
initial velocity =6,02 m·s-1
Motion from bottom to top
Downwards positive
vf2 = vi2 + 2aΔy
02 = vi2 = 0 + 2(9,8)(1,85)
vf = 6,02 m·s-1
Upwards positive
vf2 = vi2 + 2aΔy
02 = vi2 = 0 + 2(-9,8)(-1,85)
vf = 6,02 m·s-1
OPTION 4
Upwards positive/Opwaarts positief
Δy = viΔt + ½ aΔt2
0 = vi(1,23) + ½ (-9,8)(1,23)2
vi = 6,03 m·s-1
Downwards positive
Δy = viΔt + ½ aΔt2
0 = vi(1,23) + ½ (9,8)(1,23)2
vi = - 6,03 m·s-1
speed = 6,03 m·s-1
OPTION 5
Δy = (vf + vi) Δt
2
1,85 =(0 + vi) (0.62)
2
vi = 5,97 m·s-1
OPTION 6
FnetΔt = mΔv
FnetΔt = m(vf – vi)
m(9,8)(0,62) = m(0 – vi)
vi = 6,08 m·s-1
OPTION 7
(Ep + Ek)floor = (Ep + Ek)top
(mgh + ½ mv2)floor = (mgh + ½ mv2)top
0 + ½ v2 = (9,8)(1,85) + 0
v = 6,02 m·s-1 (3)
3.2.4 OPTION 1, 2, 3, 4: Marking criteria
Calculate initial velocity:
- Appropriate formula
- Substitution
Calculate Δt:
- Appropriate formula
- Substitution
- 1,97 s + Δt
- Fin answer: 2,95 – 2,97 s
Calculate initial velocity:
OPTION 1
Downwards positive
vf2 = vi2 + 2aΔy
0 = vi2 + 2(9,8)(-1,2)
vi = - 4,85 m·s-1
Upwards positive
vf2 = vi2 + 2aΔy
0 = vi2 + 2(-9,8)(1,2)
vi = - 4,85 m·s-1
OPTION 2
(Emech)top = (Emech)bot
(Ep +Ek)top = (Ep +Ek)Bot
(Any one)
(mgh + ½mv2)top = (mgh + ½mv2)Bot
(9,8)(1,2) + 0 = 0 + (½)v2
vi = 4,85 m·s-1 upwards
OPTION 3
Wnc = ΔEp + ΔEk
0 = (0 – mgh) + ½m(vf2 - vi2 )
0 = -(9,8)(1,2) + ½vi2
= 4,85 m·s-1 upwards
OPTION 4
Wnet = ΔEk
wΔxcos180° = ½mm(vf2 - vi2 )
(Any one)
(9,8)(1,2)cos180° = ½vi2
= - 4,85 m·s-1
OPTION 5
Downwards positive
Δy = viΔt + ½ aΔt2
1,2 = 0 + ½(9,8) Δt2
Δt = 0,49 s
t = 1,97 + 2(0,49)
= 2,96 s
Upwards positive
Δy = viΔt + ½ aΔt2
-1,2= 0 + ½(-9,8)Δt2
Δt = 0,49 s
t = 1,97 + 2(0,49)
= 2,96 s
Calculate time Δt
Upwards positive
Δy = viΔt + ½ aΔt2
1,2 = (4,85)Δt + ½(-9,8)Δt2
Δt = 0,4898 s / 0,5
t = 1,97 + 2(0,4898)
= 2,95 s / 2,97 s
OR
Δy = viΔt + ½ aΔt2
0 = (4,85)Δt + ½(-9,8)Δt2
Δt = 0,9898 s (or Δt = 0)
t = 1,97 + 0,9898 = 2,96 s
Downwards positive
Δy = viΔt + ½aΔt2
1,2 = (-4,85)Δt + ½(9,8)Δt2
Δt = 0,4898 s / 0,5 s
t = 1,97 + 2(0,4898)
= 2,95 s / 2,97 s
OR
Δy = viΔt + ½aΔt2
0 = (4,85)Δt + ½(9,8)Δt2
Δt = 0,9898 s (or Δt = 0)
t = 1,97 + 0,9898 = 2,96 s
OR
vf = vi + aΔt
-4,85 = 4,85 + (-9,8)Δt
Δt = 0,9898 s
Δt = 1,97 + 0,9898= 2,96 s
OR
Upwards positive
vf = vi + aΔt
0 = 4,85 + (-9,8)Δt
Δt = 0,4949 s
Δt = 1,97 + (2)(0,4949)
= 2,96 s
OR
Δy =(vi + vf)Δt
2
1.2 =(0 + 4.85) Δt Δt = 0,4948s
2
Δttotal = 2(0,4948) = 0,99 s
Δt = 1,97 + 0,99 = 2,96 s
OPTION 5: Marking criteria
- Formula
- Substitution Δy = 1,2
- Substitution 0 + ½(9,8) Δt2
- 1,97 s +
- 2 Δt
- Final answer: 2,95 - 2,97 s (6)
[15]
QUESTION 4
4.1 (Linear) momentum (of an object) is the product of mass and velocity.
(2 or 0) (2)
4.2.1
OPTION 1
East as positive
Σpi = Σpf
mpvpi + mQvQi = mpvpf + mQvQf
(Any one)
(0,16)(10) + (0,2)(-15) = (0,16)(-5) +(0,2)vQf
vQf = -3 m∙s-1
vQf = 3 m∙s-1 west
OPTION 2
West as positive
Σpi = Σpf
mpvpi + mQvQi = mpvpf + mQvQf
(Any one)
(0,16)(-10) + (0,2)(15) = (0,16)(5) +(0,2)QNf
vQf = 3 m∙s-1 west
OPTION 3
Δpp = -ΔpQ
(0,16)(-5 – 10) = -(0,2)(v – (-15))
v = -3 m·s-1
= 3 m·s-1 west (5)
4.2.2 For ball P:
West as negative
Impulse = Δp
FnetΔt = Δp
Δp = m(vPf – vPi)
= 0,16(-5 – 10)
= - 2,4
2,4 N∙s (2,4 kg∙m∙s-1)
OR
West as positive
Impulse = Δp
FnetΔt = Δp
= m(vPf - vPi)
= 0,16(5 - (-10))
= 2,4 N·s
POSITIVE MARKING FROM QUESTION 4.2.1 (3)
For ball:
West as negative
Impulse = Δp
FnetΔt = Δp
= m(vQf – vQi)
= 0,2[-3 – (-15)]
= 2,4 N∙s (2,4 kg∙m∙s-1)
OR
West as positive
Impulse = Δp
FnetΔt = Δp
= m(vQf - vQi)
= 0,16(3 – (15))
= - 2,4 N·s
2,4 N∙s (2,4 kg∙m∙s-1)
[10]
QUESTION 5
5.1 Marking criteria
If any of the underlined key words/phrases in the correct context are omitted:
- 1 mark per word/phrase. However, IF: The word “work” is omitted 0 marks
A force is non-conservative if the work it does on an object (which is moving between two points) depends on the path taken.
OR
A force is non-conservative if the work it does on an object depends on the path taken.
OR
A force is non-conservative if the work it does in moving an object around a closed path is non-zero.(2)
5.2 K = ½ mv2 /Ek = ½ mv2
ΔK = Kf - Ki
K = ½mvf2 - ½mvi2
= ½m(vf2- vi2)
=½(200)(22 - 42)
K = - 1 200 J (3)
5.3 POSITIVE MARKING FROM QUESTION 5.2.
Marking criteria/Nasienriglyne
- Appropriate formula
- Substitution into appropriate formula together with -3,40 × 103
- Final answer: 8,88 m
OPTION 1
Wnc = K + U
Wnc = ½ mvf2 - ½ mvi2 + mghf - mghi
= ½ m (vf2- vi2) + mg(hf - hi)
-3,40 × 103 = -1 200 + 200(9,8)(hf - 10)
h = 8,88 m (8,87765 m)
OPTION 2
E(mech/meg)A + Wf = E(mech)B
(Ep +Ek)A + Wf = (Ep +Ek)B
(mgh + ½mv2) A + Wf = (mgh + ½mv2)B
200(9,8)(10) + ½(200)(42) - 3,40 × 103 = 200(9,8)(h) + ½(200)(2)2
h = 8,88 m (8,87755)
OPTION 3
Wnet = ΔK
Wf + Ww = ½mvf2 - ½mvi2
Wf – ΔEp = ½mvf2 - ½mvi2
Wf - mg(hf - hi) = ½m(vf2- vi2)
-3,40 × 103 - 200(9,8)(h-10)= -1 200
h = 8,88 m (8,87755 m) (4)
5.4 OPTION 1 AND 2: Marking criteria
- Appropriate formula
- Work done by friction
- Substitution of (200)(9,8)(13,12)
- Appropriate formula
- Substitution into power formula
- Final answer: 1 814,35 W
OPTION 1
Wnc = ΔK +ΔU
Wengine + Wf = ½mvf2 - ½ mvi2 + mghf - mghi
= ½m(vf2- vi2) + mg(hf - hi)
Wengine + (50)(15)(2)cos180° = 0 + 200(9,8)(22 – 8,88)
Wengine = 27 215,20 J
Pengine = Wengine
Δt
=27 215,20
15
= 1 814,35 W
OPTION 2
Wnet = ΔK
WN + Wengine + Ww + Wf = 0
WN + Wengine - ΔEp + Wf = 0
0 + Wengine - (200)(9,8)(13,12) + (50)(2)(15)cos180° = 0
Wengine = 27 215,20 J
OR
Wnet = ΔK
WN + Wengine + Ww|| + Wf = 0
WN + Wengine +mgsinθΔxcos180o + Wf = 0
0 + Wengine - (200)(9,8)(13,12)(-1) + (50)(2)(15)cos180° = 0
Δx
Wengine = 27 215,20 J
Pengine = Wengine
Δt
= 27 215,20
15
= 1 814,35 W
OPTION 3: Marking criteria
- Appropriate formula
- Substitution of - 50
- Substitution of (-200)(9,8)(0,4373) or (-200)(9,8)(0,44)
- Appropriate formula
- Substitution into Pave = Fvave
- Final answer: 1 814,35 W - 1 824,8 W
OPTION 3
Fnet = ma
Fengine + Ffriction + Fg// = 0
Fengine + (-50) + (-200)(9,8)(0,4373) = 0
Fengine = 906,52 N (906,52 – 912,4)
Pave = Fvave
Pave = (908,52)(2)
= 1 813,04 W (1 824,8 W)
OR
W = FengineΔxcosθ
= (906,52)(30)cos0o
= 27 195,6 J (27 372 W)
P = W = 27195,6 = 1 813,04 W(1 824,8 W)
Δt 15
(5)
[14]
QUESTION 6
6.1 Marking criteria
If any of the underlined key words/phrases in the correct context are omitted:
- 1 mark per word/phrase.
The change in frequency(or pitch) (of the sound) detected by a listener because the source and the listener have different velocities relative to the medium of propagation.
OR
An (apparent) change in (observed/detected) frequency (pitch), as a result of the relative motion between a source and an observer (listener). (2)
6.2 Towards (1)
6.3
fL = v ± vL fs OR fL = v fs OR fL = v fs
v ± vs v - vs v + vs
3148 = 340 + 0 2073 = 340 - 0
340 vs 340 vs
3148(340 - vs) = 2073(340 + vs)
340 + 0 340 - 0
vs = 70 m·s-1 (69,95 - 70,16 m·s-1) (6)
6.4 POSITIVE MARKING FROM QUESTION 6.3
OPTION 1
Δt =Δx
v
Δt = 350
70
Δt = 5s
OPTION 2
Δx = viΔt + ½ aΔt2
350 = 70Δt + 0
Δt = 5 s
OPTION 3
Δx = (vi + vf)Δt
2
350 =(70 + 70) Δt
2
Δt = 5 s (2)
[11]
QUESTION 7
7.1
n = Q
e
= ( - )4 x 10 -6
( - )1,6 10-19
= 2,5 x 1013 (3)
7.2 Electrostatic force on B due to A:
FAB = kQ1 Q2
r2
=[9 x 109(4 x 10-6)(3 x 10-6)
0,2
= 2,7 N(3)
7.3 Marking criteria
If any of the underlined key words/phrases in the correct context are omitted:
- 1 mark per word/phrase.
Electric field is a region (in space) where (in which) an (electric) charge experiences a (electric) force. (2)
Ignore negative signs
7.4 Marking criteria
- Appropriate formula
- Correct substitution for A and B
- Subtraction of electric fields
- Final answer: 2,3 x106 N∙C-1
OPTION 1
Electric field at M due to: -4 x10-6 C
EAM =k Q
r2
= 9 x 109(4 x10-6)
(0,3)2
= 4,0 x 105 N∙C-1 (to left)
Electric field at M due to: +3 x 10-6 C,
EBM =k Q
r2
=9 x 109(3 x10-6)
(0,1)2
= 2,7 x106 N∙C-1 (to right)
Net electric field at M
Enet = EBM + EAM
= 4,0 x105 – 2,7 x106
= 2,3 x106 N∙C-1
(right)
OR
Net electric field at M
Enet = EBM + EAM
= -4,0 x105 + 2,7 x106
= - 2,3 x106 N∙C-1
= 2,3 x106 N∙C-1 (right)
(5)
OPTION 2
FAM = kQ1 Q2 = (9 x 109)(4 x 10-6)Q = 4 x 105Q N
r2 (0,3)2
FBM = kQ1 Q2 = (9 x 109)(4 x 10-6)Q = 2.7 x 106Q N
r2 (0,1)2
Fnet = 2,7 x 106Q + (-4 x 105Q) = 2,3 x 106Q
E = F = 2,3 x 106Q = 2,3 x 106 N·C-1 (right)
q Q
7.5 Positive (1)
7.6 POSITIVE MARKING FROM 7.2
Marking criteria
- Correct substitution into Pythagoras’s equation
- Correct substitution into Coulomb’s Law
- Correct answer(3)
(Fnet)2 = (FAD)2 + (FAB)2
(7,69)2 = (FAD)2 + (2,7)2
FAD = 7,2 N
FAD = kQ1 Q2
r2
7,2 = (9 x109)(4 x10-6)Q
(0,15)2
= 9 x109 (4 x10-6)Q
0,152
= 1,6 x 106 Q
Fnet = √FAB2 + FAD2 OR Fnet = FAB2 + FAD2
7,69 = √2,72 + (1,6x106Q)2
Q = 4,50 x10-6 C
[17]
QUESTION 8
8.1 Marking criteria
If any of the underlined key words/phrases in the correct context are omitted:
- 1 mark per word/phrase.
(Maximum) energy provided (work done) by a battery per coulomb/unit charge passing through it.
Work done by the battery to move a unit coulomb of charge across the circuit. (2)
8.2 Energy (per coulomb of charge) is converted to heat in the battery due to the internal resistance.(2)
8.3.1
I = V
R
I = 1.5
0.5
= 3 A (3)
8.3.2 OPTION 1
1 = 1 + 1
RP R1 R2
1 = 1 + 1
RP 25 15
RP = 9,375 Ω
Rext = 9,375 + 4 = 13,38
(13,375)
OPTION 2
RP = R1 R2
R1 + R2
RP = (25)(15)
25 +15
Rp = 9,375 Ω
Rext = 9,375 + 4= 13,38Ω
(13,375Ω)
(4)
8.3.3 POSITIVE MARKING FROM QUESTIONS 8.3.1 AND 8.3.2. (3)
OPTION 1
Ɛ = I(R + r)
= 3(13,38 + 0,5)
= 41,64 V (Range: 41,625 – 41,64)
OPTION 2
Ɛ = Vext + Vint
= (3)(13,38) + 1,5
= 41,64 V (Range: 41,625 – 41,64)
8.4 Yes.
For the same voltage/potential difference,a larger current will flow through a smaller resistor (I = V )
R
OR
I α 1/R , V = constant
I is inversely proportional to R and V is constant.
OR
V|| = IR
= (3)(9,38)
= 28,14 V
IR2 = V = 28,14 = 1.13A
R 25
IR3 = V = 28,14 = 1.88A
R 25
OR
V is the same
I15Ω = 25 I
40
I25Ω = 15 I
40
(3)
8.5 Remains the same(1)
[18]
QUESTION 9
9.1.1 (DC) motor/(GS-)motor (1)
9.1.2 POSITIVE MARKING FROM QUESTION 9.1.1
Electrical to mechanical /kinetic (energy) (2 or 0)(2)
9.1.3 Split ring/commutator(1)
9.1.4 Anticlockwise(2)
9.2.1 (The rms voltage/value of AC is) the AC voltage/potential difference which dissipates the same amount of energy/heat/power as an equivalent DC voltage/potential difference. (2 or 0)
ACCEPT
The rms voltage/value of AC is the DC potential difference which dissipates the same amount of energy/heat/power as AC. (2)
9.2.2 Marking criteria
- Appropriate formula for Pave
- Substitution to calculate R
- Final answer: 242 Ω
OPTION 1
P ave = Vrms2
R
200= 2202
R
R = 242 Ω
OPTION 2
P ave = VrmsIrms
200 = Irms (220)
Irms = 0,909 A (0,91)
R = Vrms or R = V
I rms I
R = 200 =
0,909
R = 242 Ω (241.76Ω)
OPTION 3
P ave = VrmsIrms
200 = Irms (220)
Irms = 0,909 A (0,91)
Pave = Irms2
R= 242 Ω
(241,76 Ω) (3)
9.2.3 Marking criteria for options 1,2 and 3
- Appropriate formula to calculate P or Irms
- Substitution
- Formula for P or W containing Δt
- Substitution
- Final answer: 55 785,12 J
POSITIVE MARKING FROM QUESTION 9.2.2.
OPTION 1
Marking criteria
- Appropriate formula for W containing V
- Substitution
- Final answer: 55 785,12 J (5)
W = V2 Δt
R
= (1502) (10 x 60)
242
= 55 785,12 J
OPTION 2
Pave = V2rms
R
= 1502
242
Pav = 92,975 W
P = W
Δt
92,975 = W
(10)(60)
W = 55 785,12 J
(55785,12 – 55896 J)
OPTION 3
Pave = V2rms
R
242 = 150
I rms
I rms = 0,620 A
W = I2RΔt
= (0,62)2(242)(10)(60)
= 55 785,12 J
(55785,12 – 55896 J)
OR
w = VIΔt
= (150)(0,62)(600)
= 55 800 J
OPTION 5
P ave = V2rms =1502 = 92,975 W
R 242
Pave = Irms2R
92,975 = Irms2 (242)
Irms = 0,6198 A
W = I2RΔt
= (0,6198)2(242)(10)(60)
= 55 778,88 J
[16]
QUESTION 10
10.1 Photoelectric effect(1)
10.2 Work function (of potassium)(1)
10.3 Potassium
It has the lowest work function / threshold frequency / highest threshold wavelength. (2)
10.4 Marking criteria/Nasienriglyne
If any of the underlined key words/phrases in the correct context are omitted:
- 1 mark per word/phrase.
The work function of a metal is the minimum energy that an electron (in the metal) needs to be emitted/ejected from the metal / surface. (2)
10.5.1 Wo= hfo
= (6,63 x 10-34)(1,75 x 1015)
= 1,160 x 10-18 J
OR
E = Wo + Ek(max)
hf = Wo + Ek(max)
(6,63 x 10-34)(1,75 x 1015) = Wo + 0
Wo = 1,160 x 10-18 J (3)
10.5.2 POSITIVE MARKING FROM QUESTION 10.5.1.
E = Wo + Ek(max)
hf = hfo + ½mv2
(6,63 x 10-34)f = 1,160 x 10-18 + (9,11 x 10-31) (5,60 x 105)2
f = 1,97 x 1015 Hz (4)
[13]
TOTAL: 150