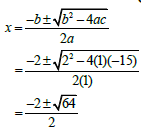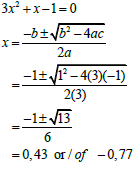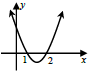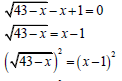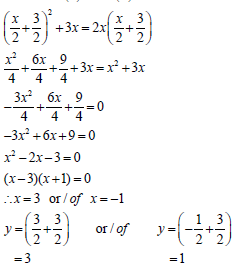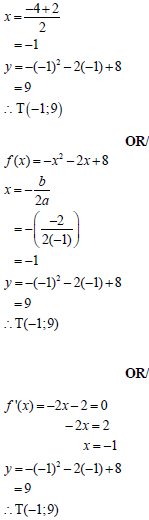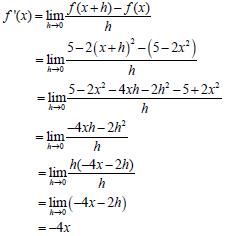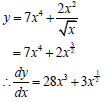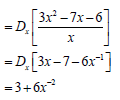Mathematics Paper 1 Memorandum - Grade 12 September 2021 Preparatory Exams
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupNOTE:
- If a candidate answers a question TWICE, mark the FIRST attempt
- Consistent accuracy applies in ALL aspects of the marking
- If a candidate crossed out an attempt of a question and did not redo the question, mark the crossed-out
- The mark for substitution is awarded for substitution into the correct
MEMORNDUM
QUESTION 1
1.1.1 | x2 + 2x -15 = 0 OR
| ? factors OR ? substitution | |||||
1.1.2 |
Penalise 1 mark for incorrect rounding | ? substitution ? x = 0, 43 ? x = -0, 77 (3) | |||||
| 1.1.3 | x(x - 3) ≥ -2
| ? standard form ? factorisation ? x ≤ 1 or/of ? x ≥ 2 (4) | |||||
| 1.1.4 |
| ? isolating the surd ? squaring both sides ? standard form ? factorisation ? selection (5) | |||||
1.2 | 2y - x = 3 (1) x = 2y - 3 (3) ∴ y = 3 or y = 1 OR | ? x = 2y - 3 ? substitution ? standard form ? factorisation ? y-values
OR ? y = x + 3 ? substitution ? standard form ? factorisation ? x-values ? y-values (5)
|
| 1.3 |
For non-real roots:
OR
| ? Δ< 0 ? standard form ? factorisation ? answer
OR
? Δ< 0 ? standard form ? factorisation ? answer (4) |
| [24] |
QUESTION 2
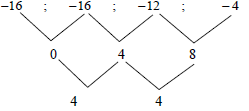
| 2.1.1 |
8 | ? 8 (1) |
| 2.1.2 | 2a = 4 | ? a = 2 ? b = -6 ? c = -12 ? Tn = 2n2 - 6n -12 (4) |
| 2.1.3 | T38 = 2(38)2 - 6(38) -12 | ? substitution ? answer (2) |
2.1.4 | General term for first differences: Tn(linear) = (Tn+1 - Tn )(quadratic) OR 2(n +1)2 - 6(n +1) -12 - (2n2 - 6n -12) = 400 OR Trialand error | ? Tn = 4n - 4 ? Tn = 400 ? answer OR ? 4n - 4 = 400 ? ? answer OR ?subst. for T101 and T102 ? 400 ? answer (3) |
2.2.1 | Tn = a + (n -1)d | ? substitution ? answer (2) |
| 2.2.2 | 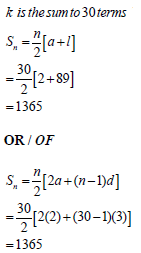 | ? Sum formula ? substitution ? answer OR ? Sum formula ? substitution ? answer (3) |
| [15] |
QUESTION 3
3.1 | T9 = ar8 = 768 | ?ar12 = 12 288 ? r =± 2 ? value of a | (3) | ||
3.2.1 | S2 = 54 - 24 | ? answer | (1) | ||
| 3.2.2 | T1 + T2 = 30 | ? a + ar = 30 19 | (1) | ||
3.2.3 | S∞ = a = 54 | ? a = 54(1- r) ? equating ?r2 = 4/9 ? answer | (4) | ||
[9] | |||||
QUESTION 4
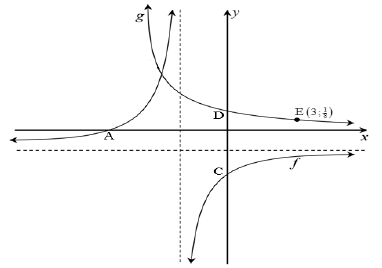 | ||||
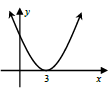
4.1 | D(0 ; 1) | ? (0 ; 1) | (1) | |
4.2 | x = -2 ; y = -1 | ? x = -2 ? y = -1 | (2) | |
4.3 | ? ∈ R but ? # −2 | ? ? ∈ R ?? # −2 | (2) | |
4.4 | g(x) = bx | ? substitution ? answer | (2) | |
4.5 | y = -3 -1 y = -3 -1 | ? substitution y = 0 ? x = -5 ? y =- 5 | (3) | |
| 4.6 |
OR y = 2-x | ? OR ? x = 2- y ? y = -log2 x | (2)
(2) | |
| 4.7 | ||||
| 4.7.1 | -5 < x < -2 OR x ∈(-5 ; - 2) | ?? answer (A) | (2) | |
| 4.7.2 | 0 < x ≤ 1/8 OR x ∈(0 ; 1/8 ] | ?? answer (A) | (2) | |
| [16] | ||||
QUESTION 5
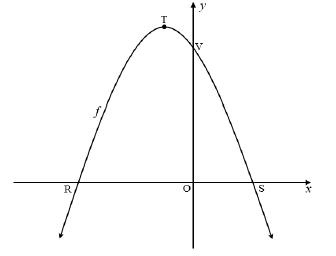 | |||||
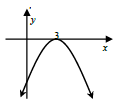
| 5.1 | -x2 - 2x + 8 = 0 | ? f (x) = 0 | (4) | ||
5.2 |
| ? method ? x = -1 ? y = 9 OR ? - b ? x = -1 ? y = 9 OR ? -2x - 2 = 0 ? x = -1 ? y = 9 | (3) | ||
5.3.1 | f (x) = -x2 - 2x + 8 | ? f / (x) ? f / (x) = 2 ? x = -2 ? y = 8 | (4) | ||
5.3.2 | g(x) = mx + c | ? gradient ? equation | (2) | ||
| 5.4 | f (x) = -x2 - 2x + 8 OR h(x) = (x + 3)(x - 3) OR New turning point = (0 ; –9) | ? - f (x -1) OR ?? roots 3 and –3 OR ? (0 ; ??–9) | (4) | ||
| 17] | |||||
QUESTION 6
| 6.1 | 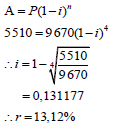 | ? subst. into correct formula |
6.2 | 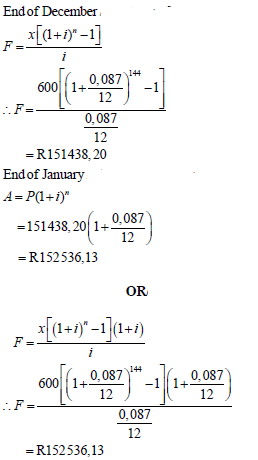 | ? n = 144 ? subst. into correct formula ? adding final month’s interest ? answer OR ? n = 144 ? subst. into correct formula ? adding final month’s interest ? answer (4) |
6.3.1 | 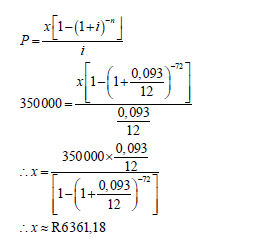 | ? i = 0, 093 and n = 72 ? substitution into correct formula ? answer (3) |
| 6.3.2 | 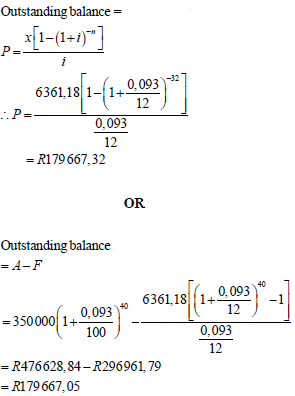 | ? i = 0,093 and/en n = 32 OR ? i = 0,093 and/en n = 40 ? P = 179 667, 32 (3) |
| 6.3.3 |  | ? subst. into correct formula ? correct use of logs ? = 28,73 ? n = 29 months OR ? subst. into correct formula ? correct use of logs ? = 28,73 ? n = 29 months (4) |
| [17] |
QUESTION 7
7.1 |
| ? substitution ? expansion ? simplification ? notation and lim (-4x - 2h) ? answer (5) |
7.2.1 |
| ? 2x½ ? 28x3 ? 3x½ (3) |
7.2.2 |
| ? 3x - 7 ? -6x-1 |
[12] |
QUESTION 8
8.1.1 | f (x) = 2(x - x1 )(x - x2 )(x - x3) | ?? f (x) = 2( x +1)( x - ½ )( x - 3) OR ?? f (x) = ( x +1)(2x -1)( x - 3) | |||
8.1.2 | f '(x) = 6x2 -10x - 4 | ? f '( x) = 6x2 -10x - 4 = 0 | (4) | ||
8.1.3 (a) | - 1/3 < x < 2 | ?? answer | (2) | ||
8.1.3 (b)
| 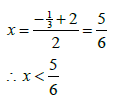 | ? f ''(x) =12x -10 OR ? x = 5/6
| (3) | ||
| 8.2 | 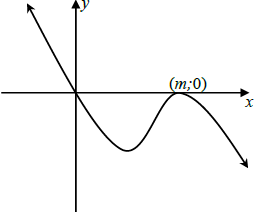 | ? f (0) = 0 | (3) | ||
[16] | |||||
QUESTION 9
9.1 | A = (½ ×15x × 8x × 2) + (15xy) + (8xy) + (17xy) | ? total surface area | (2) |
9.2 | V = (½b.h) × H | ? substitution into V ? substituing for y | (2) |
9.3 | V '(x) = 8640 - 540x2 | ? V '(x) = 8640 - 540x2 | (4) |
[8] | |||
QUESTION 10
10.1.1 | P(B) = 1- P(not) | ? 0,55 (1) |
10.1.2 | P(A and/en B) = P(A)×P(B) P(A or B) = P(A) + P(B) - P(A and B) | ? P(A)×P(B) |
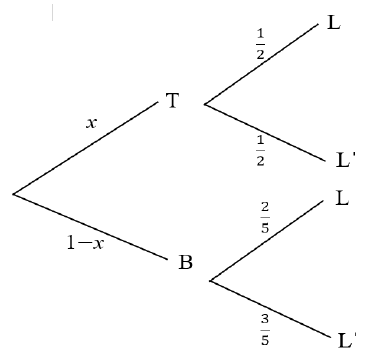
10.2 |
P(late) = 1/2 x + 3/5(1- x) |
? 1/2 x + 3/5(1- x) ? equating ? substitution ? answer (4) |
[8] |
QUESTION 11
| 11.1 | 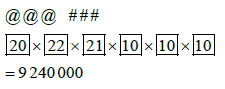 | 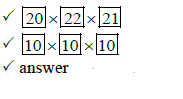 |
| 11.2 | 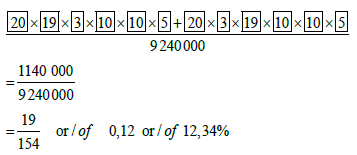 | 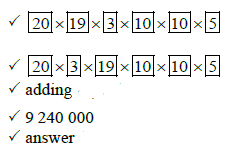 |
| [8] |
TOTAL: 150