Physical Sciences Paper 1 Memorandum - Grade 12 September 2021 Preparatory Exams
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupGENERAL GUIDELINES
- CALCULATIONS
1.1 Marks will be awarded for: correct formula, correct substitution, correct answer with unit.
1.2 No marks will be awarded if an incorrect or inappropriate formula is used, even though there are many relevant symbols and applicable substitutions.
1.3 When an error is made during substitution into a correct formula, a mark will be awarded for the correct formula and for the correct substitutions, but
no further marks will be given.
1.4 If no formula is given, but all substitutions are correct, a candidate will forfeit one mark.
1.5 No penalisation if zero substitutions are omitted in calculations where correct formula/principle is correctly given.
1.6 Mathematical manipulations and change of subject of appropriate formulae carry no marks, but if a candidate starts off with the correct formula and then changes the subject of the formula incorrectly, marks will be awarded for the formula and correct substitutions. The mark for the incorrect numerical answer is forfeited.
1.7 Marks are only awarded for a formula if a calculation has been attempted, i.e. substitutions have been made or a numerical answer given.
1.8 Marks can only be allocated for substitutions when values are substituted into formulae and not when listed before a calculation starts.
1.9 All calculations, when not specified in the question, must be done to a minimum of two decimal places.
1.10 If a final answer to a calculation is correct, full marks will not automatically be awarded. Markers will always ensure that the correct/appropriate formula is used and that workings, including substitutions, are correct.
1.11 Questions where a series of calculations have to be made (e.g. a circuit diagram question) do not necessarily always have to follow the same order. FULL MARKS will be awarded provided it is a valid solution to the problem. However, any calculation that will not bring the candidate closer to the answer than the original data, will not count any marks. - UNITS
2.1 Candidates will only be penalised once for the repeated use of an incorrect unit within a question.
2.2 Units are only required in the final answer to a calculation.
2.3 Marks are only awarded for an answer, and not for a unit per se. Candidates will therefore forfeit the mark allocated for the answer in each of the following situations:
• Correct answer + wrong unit
• Wrong answer + correct unit
• Correct answer + no unit
2.4 SI units must be used except in certain cases, e.g. V.m-1 instead of N.C-1, and cm•s-1 or km•h-1 instead of m•s-1 where the question warrants this. - GENERAL
3.1 If one answer or calculation is required, but two are given by the candidate, only the first one will be marked, irrespective of which one is correct. If two answers are required, only the first two will be marked, etc.
3.2 For marking purposes, alternative symbols (s, u, t, etc.) will also be accepted.
3.3 Separate compound units with a multiplication dot, not a full stop, for example, m•s-1.
For marking purposes, m•s-1 and m/s will also be accepted. - POSITIVE MARKING
Positive marking regarding calculations will be followed in the following cases:
4.1 Sub-question to sub-question: When a certain variable is calculated in one sub-question (e.g. 3.1) and needs to be substituted in another (3.2 of 3.3),
e.g. if the answer for 3.1 is incorrect and is substituted correctly in 3.2 or 3.3, full marks are to be awarded for the subsequent sub-questions.
4.2 A multistep question of a sub-question: If the candidate has to calculate, for example, current in die first step and gets it wrong due to a substitution error, the mark for the substitution and the final answer will be forfeited. - NEGATIVE MARKING
Normally an incorrect answer cannot be correctly motivated if based on a conceptual mistake. If the candidate is therefore required to motivate in QUESTION 3.2 the answer given in QUESTION 3.1, and QUESTION 3.1 is incorrect, no marks can be awarded for QUESTION 3.2. However, if the answer for e.g. QUESTION 3.1 is based on a calculation, the motivation for the incorrect answer could be considered.
MEMORANDUM
QUESTION 1:
MULTIPLE-CHOICE QUESTIONS
1.1 C ?? (2)
1.2 A ?? (2)
1.3 B ?? (2)
1.4 D ?? (2)
1.5 D ?? (2)
1.6 C ?? (2)
1.7 A ?? (2)
1.8 C ?? (2)
1.9 D ?? (2)
1.10 B ?? (2) [20]
QUESTION 2
2.1.1 When a (non-zero) resultant/net force acts on an object, it accelerates in the direction of the force. The acceleration is directly proportional to the force and inversely proportional to the mass of the object. ?? (2)
2.1.2
| OPTION 1 | OPTION 2 |
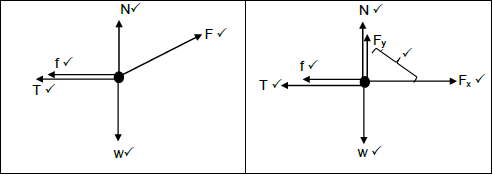 | |
(5)
Accept the following symbols: | |
N | FN/Normal/Normal force |
f | Ff / fk / fr / frictional force/kinetic frictional force / |
w | Fg,/mg/weight/FEarth on block/49 N/gravitational force/ |
T | Tension / FT / Fs |
Fapplied | F / FA / Applied force |
- Marks awarded for arrow and label
- Do not penalise for length of arrows since drawing is not drawn to scale.
- Any other additional force(s) 3/4
- If force(s) do not make contact with body. Max.3/4.
2.1.3
OPTION 1 | OPTION 2 |
Fnet = ma Any one ? | Fnet = ma Any one ? |
2.2 F = Gm1m2 ?
d2
1 842,50 ? = (6,67 × 10-11 )( 5,98 ×1024 )(200) ?
d2
d = 6 579 982,80 m
distance above earth surface
= 6 579 982,80 – 6,38 x 106 ?
= 199 982,80 m (1,9998280 x 105 m / 2,00 x 105 m) ? (5)
[17]
QUESTION 3
3.1.1 OPTION 1
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf2 = vi2 + 2aΔy ? | vf2 = vi2 + 2aΔy ? |
OPTION 2
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf = vi + aΔt | vf = vi + aΔt |
OPTION 3
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf = vi + aΔt | vf = vi + aΔt |
OPTION 4 (ACCEPT) | |
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf = vi + aΔt | vf = vi + aΔt |
(3)
3.1.2
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf = vi + aΔt ? | vf = vi + aΔt ? |
(5)
3.1.3
OPTION 1 | |
Positive marking from 3.1.1 | |
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf2 = vi2 + 2aΔy ? | vf2 = vi2 + 2a∆? ? |
OPTION 2 | |
Positive marking from 3.1.1 | |
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf = vi + aΔt | vf = vi + aΔt |
OPTION 3 | |
Positive marking from 3.1.1 | |
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf = vi + aΔt | vf = vi + aΔt |
OPTION 4 | |
Positive marking from 3.1.1 | |
UPWARDS POSITIVE | UPWARDS NEGATIVE |
vf = vi + aΔt | vf = vi + aΔt |
(4)
3.2 Positive marking from 3.1.1 and 3.1.2 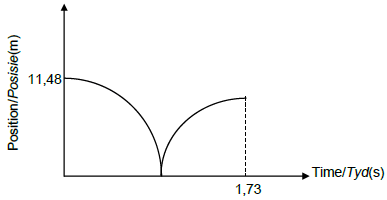
CRITERIA FOR MARKING | |
Correct shape | ? |
Height indicated(11,48 m) | ? |
Time t indicated (1,73 s) | ? |
(3) [15]
QUESTION 4
4.1 In an isolated system total linear momentum is conserved. ?? (2)
4.2.1
- ∑pi = ∑pf
mAviA + mBviB = (mA + mB)vf Any one ?
(2 x viA) + (4 x -5) ?= (2+4)(-1,67) ?
viA = 4,99 m.s-1 (East) ? (4)
4.2.2
POSITIVE MARKING FROM 4.2.1 | POSITIVE MARKING FROM 4.2.1 | ||
OPTION 1 | OPTION 2 | ||
Fnet.∆t = ∆p | Any one? | Fnet.∆t = ∆p | Any one ? |
Fnet x 0,01? = 2 (-1,67- 4,99) ? Fnet = - 1 332 N Fnet = 1 332 N west/left ? | Fnet x 0,01? = 2 [1,67- (-4,99)] ? Fnet = - 1 332 N Fnet = 1 332 N west/left ? | ||
OPTION/OPSIE 3 | OPTION/OPSIE 4 | ||
Fnet = ma | Any one? | Fnet = ma | Any one ? |
Fnet = 2 x ( - 1,67 - 4,99?) | Fnet = 2 x ( 1,67 - (- 4,99)?) | ||
OPTION 5 | OPTION 6 | ||
Fnet.∆t = ∆p Fnet.∆t = m(vf – vi) | Any one ? | Fnet.∆t = ∆p Fnet.∆t = m(vf – vi) | Any one ? |
Fnet(0,01) ? = 4(-1,67 – -5) ? Fnet = 1 332 FAB = - FBA Fnet(BA) = 1 332 N west/left ? | Fnet(0,01) ? = 4(1,67 – 5) ? Fnet = -1 332 FAB = - FBA Fnet(BA) = 1 332 N west/left ? | ||
(4) [10]
QUESTION 5
5.1 Gravitational force ? (1)
5.2
- ∆x = 12 ? = 24 m
sin30º
Wf = f.∆x cos θ ?
Wf = 35,5 x 24 cos 180º ?
Wf = - 852 J ? (4)
5.3 Zero/0 J ? (1)
5.4 Positive marking from 5.2
OPTION 1
- Wnet = ∆Ek Any one?
Wf + WF + WFg = ∆Ek
f x ∆x cos θ + F∆xcos θ + mg(h2 – h1) = ∆Ek
-852 ? + (62,5 x 24 cos180o) ? + m(9,8)(12-0) ? = 0
m = 20 kg ?
OPTION 2
- Wnc = ∆Ep + ∆Ek
Wf + WF = ∆Ep + ∆Ek Any one ?
f∆xcosθ + F∆xcos = mg(h2 – h1) + ∆Ek
-852 ?+ (62,5)(24)cos180o ?= m(9,8)(0 – 12) ?+ 0
m = 20 kg ?
OPTION 3
- Wnet = ∆Ek
Wf + WF + Ww = ∆Ek Any one?
f∆xcosθ + F∆xcos θ + mgΔxcosθ = ∆Ek
-852 ? + (62,5)(24)cos180o ? + m(9,8)(24)cos60o ? = 0 m = 20 kg ?
(5) [11]
QUESTION 6
6.1.1 520 Hz / 520 waves per second (waves.s-1)? (1)
6.1.2
- The change in frequency ?(or pitch) observed/detected by a listener because the listener and the sound source have different velocities relative to the medium of sound propagation. ?
OR - The (apparent) changed in observed/detected frequency (pitch) as a result of relative motion between the sound source and the listener. ? ? (2)
6.1.3 TOWARDS ? Detected frequency is higher than the source frequency ? (2)
6.1.4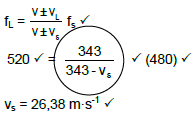 (5)
(5)
6.1.5 Decreases ?
- For a constant velocity/speed of sound, if the frequency increases, λ decreases. ?
OR - λ α 1/f at constant velocity/speed/by konstante snelheid/spoed ?
OR - f α 1/λ at constant velocity/speed/by konstante snelheid/spoed ? (2)
6.2 Light from the star is shifted towards longer wavelength (towards the red end of the spectrum) ?which indicated that the star is moving away from the earth. ? (2)
6.3
- Used to measure the direction and speed of blood flow in arteries and veins. ?
OR - Used to measure the heartbeat of a foetus in the womb. (1)
[15]
QUESTION 7
7.1.1 GAIN ? (1)
7.1.2
- n = Q ?
qe
n = 5 x 10-6 ?
1,6 x 10-19
n = 3,125 x 1013 (electrons) ? (3)
7.1.3
- E = kQ ?
r2
E = 9 x 109 x 5 x 10-5 ? ?
0,12
E = 4,5 x 106 N.C-1 ? left ? (5)
7.2.1 Negative ?
- Like charges repel each other ?
OR - The charges repel each other. If sphere A is negative, then sphere B must also be negative. ? (2)
7.2.2
- FE = Tsin30º
FE = 25sin30º ?
FE = 12,5 N
FE = kQ1Q2 ?
r2
12,5 ?= (9 × 109 )( 5 × 10-6 ) Q ?
0,052 ?
Q = 6,94 x 10-7 C ? (6)
[17]
QUESTION 8
8.1.1
- Temperature?
- Length of the conductors? (Any two)
- Thickness of the conductors
ACCEPT: Type of material (2)
8.1.2
- Gradient is the inverse of the resistance. ?/
OR - Gradient = 1 ? (1)
R
8.1.3 Conductor C. ?
- It has the highest resistance. The higher the resistance of a conductor, the more heat is produced in the conductor if the current is constant. ? (2)
8.2.1
- R = ? ?
?
R = 12 ?
1,5
R = 8 Ω ? (3)
8.2.2
- OPTION 1 OPTION 2
Rtotal = R + r ? ε = I(R+ r) ?
[8 = (4 + 3) ?+ r ]? 12 = 1,5 [(4 + 3) ?+ r] ?
r = 1 Ω ? r = 1 Ω ?
(4)
8.2.3
- W = I2R∆t ?
W = (1,5)2(3)(180) ?
W = 1 215 J ? (3)
8.3.1 Decrease? (1)
8.3.2 Increase ? (1)
8.4 Increase ?
Rext decreases. Current through battery increases. ?
W = I2r∆t / Energy transfer to the battery/work done by battery increases. ? (3)
[20]
QUESTION 9
9.1 Mechanical energy to electrical energy. ?? (2)
9.2 AC generator has slip rings and DC generator has a split ring / commutator ? (1)
9.3
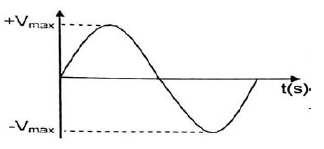
CRITERIA FOR MARKING | |
Correct shape | ? |
Axes labelled correct | ? |
Vmax indicated on graph | ? |
(2)
9.4
 (4)
(4)
9.5 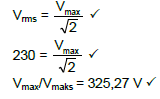 (3)
(3)
[12]
QUESTION 10
10.1 Work function (of the metal) ?
- Ek(max) = hc – W0 ?
λ
The intercept on the vertical axis = Wº ?
OR - hc = W0 + Ek(max) ?
λ
The intercept on the vertical axis is equal to the Wº ? (3)
10.2
- E = W0 + Ek(max)
hf = W0 + Ek(max) Any one ?
hf = hf0 + Ek(max)
6,63 x 10-34 x 6,16 x 1014? = 6,63 x 10-34 f0 ? + 5,6 x 10-20 ?
f0 = 5,32 x 1014 Hz ? (5)
10.3.1
- Remain the same/Bly dieselfde ?
The gradient is equal to the product of Planck’s constant and the speed of light in vacuum which are constants. ?
OR
Gradient = hc, which are constants (2)
10.3.2 Remains the same ?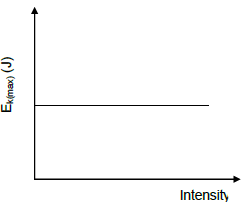
| CRITERIA FOR MARKING | |
| Axes labelled | ? |
| Correct shape | ? |
(3) [13]
TOTAL: 150