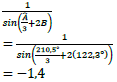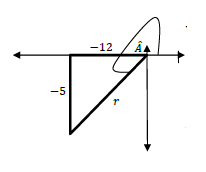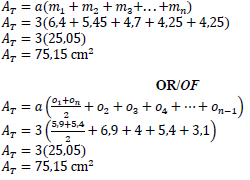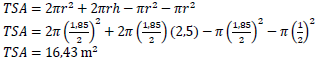Technical Mathematics Paper 2 Memorandum - Grade 12 September 2021 Preparatory Exams
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupNOTE:
- Continuous accuracy (CA) applies only where indicated in this marking
- Assuming values/answers in order to solve a problem is
MARKING CODES | |
M | Method |
A | Accuracy |
AO | Answer only |
CA | Consistent accuracy |
F | Formula |
I | Identity |
R | Rounding |
S | Simplification |
ST | Statement |
RE | Reason |
ST RE | Statement and correct reason |
SF | Substitution correctly in correct formula |
NPU | No penalty for omitting units |
MEMORANDUM
QUESTION 1
Q | M | |
| ||
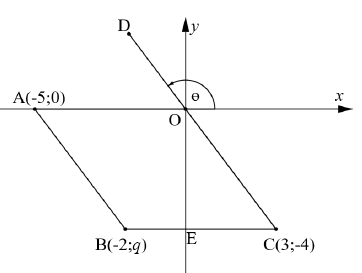
1.1 | ? = −4 | √ A (1) |
1.2 | ??2 = (−2 + 5)2 + (−4 − 0)2 | √ M |
1.3 | ??? = −4−0 | √ − 4 A 3 √ 53,13° CA √ 126,87° CA (3) |
1.4 | ?? = 3 − (−2) = 3 + 2 = 5 units | √ ?? & ?? M |
[10] |
QUESTION 2
Q | M | ||
2.1.1 | ?2 + ?2 = 25 … 1 | √ ? = ? + 1 | |
2.1.2 | (3; 2): (3)2 + (2)2 = 13 | √ 13 | |
2.1.3 | ???? = 0−3 | √ − 3/4 √ 4/3 √ 25/3 = ? √ ? = 4/3 ? + 25/3 CA (4) | |
2.2 | 36?2 + 49?2 = 1764 |
| √ ?2 + ?2 = 1 |
[18] | |||
QUESTION 3
Q | M | ||||||||
3.1.1 |
| √ SF √ −0,8 | (2) | ||||||
3.1.2 |
| √ 1 √ SF √ −1,4 | (3) | ||||||
3.2.1 | ????̂ = 5 = −5 OR ????̂ = 5 = −5 |
r2 = (-12)2 + (-5)2 | √ ???? = 5 = −5 A √ correct quadrant √ ? = 13 A √ 1 or ?????2?̂ = (13/-5)2 CA √ 169/25 CA (5) | ||||||
3.2.2 | ????̂ − ????̂ = 1 − ????̂ | OR ????̂ − ????̂ = 1 − ????̂ | √ 1 ?? 13 √ 1 √ −109 CA (3) | ||||||
3.2.3 | ????̂ = 5/12 ?̂ = 202,62° | √ method √ 22,62° √ 202,62° | (3) | ||||||
[16] | |||||||||
QUESTION 4
Q | M | |
4.1 | ???(? − ?). ?????(2? − ?). ???(? + ?) | √ correct conversion of rad to degrees √ ???(?) √ − 1 √ ???(?) √ 1 √ ???(?) √ −1.???(?) √ −tan (?) (8) |
OR | ||
???(? − ?). ?????(2? − ?). ???(? + ?) | √ correct conversion of rad to degrees | |
4.2 | ???/?? = ???? − ???? | √ ????
|
[13] | ||
QUESTION 5
Q | M | ||||
5.1 | 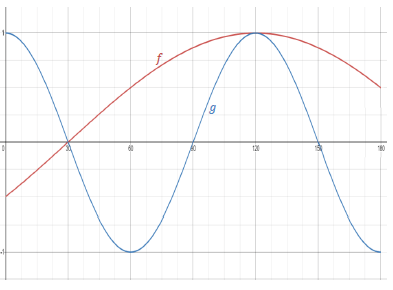 | √ cos start and end point √ cos turningpoints √ cos ?- intercepts √ sin start and end point √ sin turningpoints √ sin ?- intercepts (6) | |||
5.2.1 | 120° | √ 120° | (1) | ||
5.2.2 | (a) | ? = 30° and / en ? = 120° | √ ? = 30° √ ? = 120° | (2) | |
(b) | 90° ≤ ? ≤ 150° | √ 90° ≤ √ ≤ 150° | (2) | ||
[11] | |||||
QUESTION 6
Q | M | |
| ||
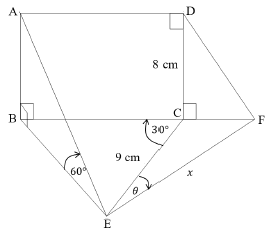
6.1 | AB = 8 cm (opp sides of rec = ) | √ 8 cm ST |
6.2 | ?? = tan 30° | √ ?? = tan 30° M |
6.3 | sin ??̂? = sin 30° | √ SF |
6.4 | ??̂? = 180° − 30° − 77° | √ ST RE |
6.5 | ??2 = ??2 + ??2 − 2(??)(??) cos ??̂? | √ (9)2 + (10)2 − 2(9)(10) cos(25°) SF |
[13] |
QUESTION 7
Q | M | ||
7.1 | double the size of the angle subtended by the same arc at the circumference of a circle | (1) | |
7.2 | | ||
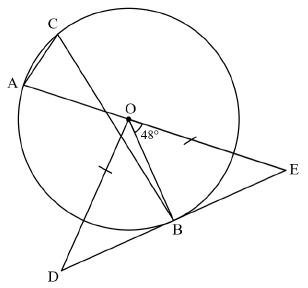
7.2.1 | ??̂? = 180° − 48° …(suppl. ∠’s) | √ ST RE | (1) |
7.2.2 | ?̂ = ½ (132°)…( ∠ at centre = 2 x ∠ at circum.) | √ RE √ 66° ST | (2) |
7.2.3 | ??̂? = 90° …( tan ⊥ rad) | √ ST √ RE √ ST RE | (3) |
7.2.4 | ?̂ = ??̂? = 42° …(∠′s opp.= sides) | √ ST RE √ ST RE | (2) |
7.2.5 | ??2 = ??2 − ??2 ….(Pythagoras) | √ M Pythagoras √ ST ??2 = 24 √ ST ?? = √24 | (3) |
[12] | |||
QUESTION 8
Q | M | |
8.1 | supplementary | √ (1) |
8.2 |
| |
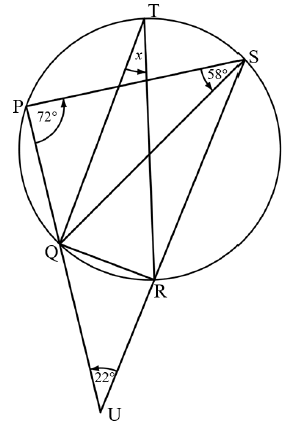
8.2.1 (a) | ??̂? = ?̂ = ? (∠′s subt.chord QR ) | √ ST √ RE (2) |
8.2.2 (b) | ??̂? = 180° − (58° + ?) (opp. ∠′s quad.) = 122° − ? | √ ST RE |
8.2.2 | ?̂ + ??̂? + ??̂? = 180° (int. ∠′s ∆) | √ ST RE |
OR | OR | |
?̂ + ?̂ + ?̂ = 180° (int. ∠′s ∆) | √ ST RE | |
[8] |
QUESTION 9
Q | M | |
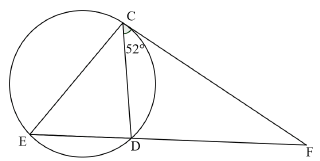
9.1 |
| √ ST |
9.2 | | |
9.2.1 | In ∆??? and ∆???: | √ ST RE |
9.2.2 | ?? = ?? = ?? (∆???⦀∆???) | √ ?? = ?? = ?? ST |
9.2.3 | ?? = 15 − 6 = 9 | √ ?? = 9 A |
OR | OR | |
??2 = 15 × 9 (from 9.2.2) | √ ??2 = 15 × 9 A | |
9.2.4 | ?? = 12 = 4 | √ 12 SF A |
9.2.5 | ??̂? = 44° + 52° = 96° ≠ 90° | √ ST |
| OR | ||
??̂? = 180° − 44° − 52° = 86° ≠ 90° | √ ST √ ST RE (2) | |
| [16] | ||
QUESTION 10
Q | M | ||
10.1 | | ||
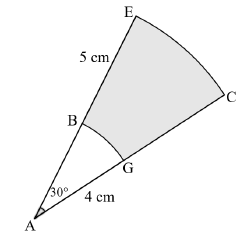
10.1.1 | ?̂ = 30° × ? | √ × ? | |
10.1.2 | ? = ?? | √ F | (3) |
10.1.3 | Area of a sector / ??? ??? ′? ?????? = ?2? | √ F | (3) |
10.1.4 | Area of a sector / ??? ??? ′? ?????? = ?2? | √ SF | (4) |
10.2 | | |
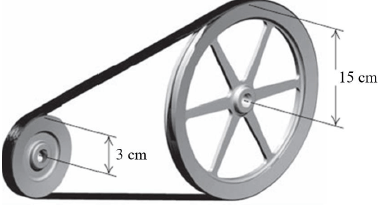
10.2.1 | ? = 2?? | √ F |
10.2.2 | ? = ??? | √ F |
OR | OR | |
? = ?? | √ F | |
10.2.3 | Linear speed of large pulley | √ F |
10.3 | | |
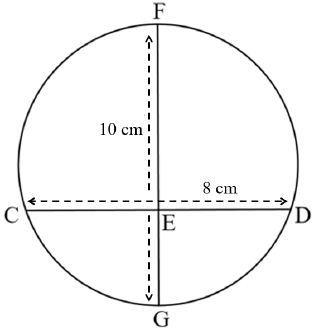
4ℎ2 − 4?ℎ + ?2 = 0 | √ F | |
OR | OR | |
?? = 4 (line from centre perpendicular to chord) | √ ST RE √ ST RE √ ??2 = (5)2 − (4)2 SF √ ?? = 3 cm CA √ ?? = 2 cm CA (5) | |
[26] | ||
QUESTION 11
Q | M | ||
11.1 |  | ||
| √ F OR √ F | ||
11.2 | | ||
| √ F | (3) | |
[7] | |||
TOTAL: | 150 | ||