MATHEMATICAL LITERACY PAPER 1 GRADE 12 QUESTIONS - NSC EXAMS PAST PAPERS AND MEMOS NOVEMBER 2020
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICAL LITERACY PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2020
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions. Answer ALL the questions.
- 2.1 Use the ANNEXURES in the ADDENDUM to answer the following questions:
- ANNEXURE A for QUESTION 2.1
- ANNEXURE B for QUESTION 2.3.4
- ANNEXURE C for QUESTION 3.2
- ANNEXURE D for QUESTION 4.1
2.2 Answer QUESTION 5.2.4 on the attached ANSWER SHEET.
2.3 Write your centre number and examination number in the spaces on the ANSWER SHEET. Hand in the ANSWER SHEET with your ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Start EACH question on a NEW page.
- You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
- Show ALL calculations clearly.
- Round off ALL final answers appropriately according to the given context, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Maps and diagrams are NOT necessarily drawn to scale, unless stated otherwise.
- Write neatly and legibly.
QUESTION 1
1.1 The information below represents three meal options for the same meal.
- Mr Delivery
- Uber Eats
- Restaurant menu

Use the above information to answer the questions that follow.
1.1.1 Identify the type of graph used.
1.1.2 Calculate A, the total for the restaurant menu.
1.1.3 Calculate B, the delivery fee for Mr Delivery.
1.1.4 Write down the difference between the highest price and the lowest price of the meal, excluding delivery/gratuity.
1.1.5 If the delivery fee for Uber Eats increases by 6,32%, calculate (in rand) the increase in the delivery fee.
1.2 The two line graphs below represent the average petrol and diesel prices per litre for the period 2003 to 2013.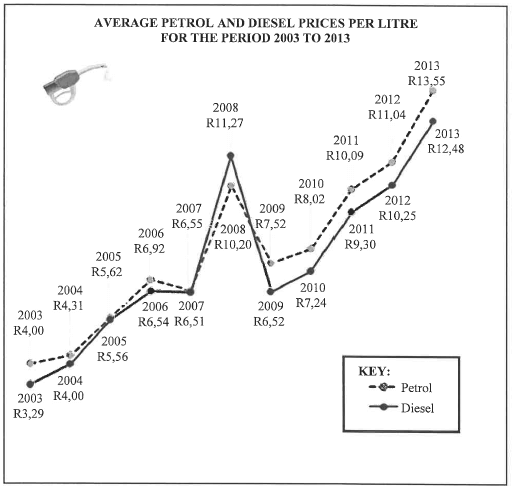
Use the above information to answer the questions that follow.
1.2.1 Write down the year in which the diesel price was higher than the petrol price.
1.2.2 Calculate the difference between the price of petrol in 2012 and in 2004.
1.2.3 Determine, to TWO decimal places, the unit ratio of the diesel price in 2005 to the diesel price in 2013.
1.2.4 Calculate the total cost of 13,45 litres of petrol in 2003.
1.2.5 Write down the year in which the difference between the petrol price and the diesel price was less than five cents.
1.3 Devashni will be travelling from Cape Town to Port Elizabeth to visit her grandmother. She will use the map below to plan her journey.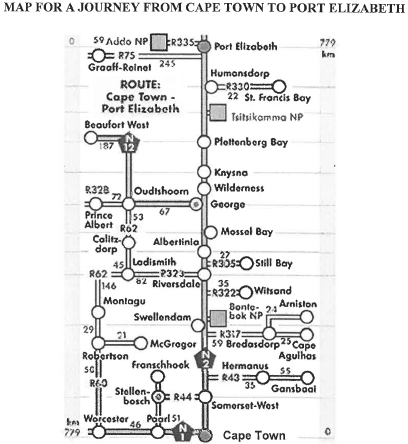
Use the above map to answer the questions that follow.
1.3.1 Identify the type of map used above. (2)
1.3.2 Determine, in metres, the actual distance between Cape Town and Port Elizabeth. (2)
1.3.3 Along the route Devashni will visit a friend in Oudtshoorn. At Riversdale she will take a detour via the R323 to Oudtshoorn.
- Name the towns she will pass when traveling from Riversdale to Oudtshoorn. (2)
- Calculate the total distance she will travel from Riversdale to Oudtshoorn. (2)
[30]
QUESTION 2
2.1 Dean Peterson has a clothing account at Markham clothing store. At Markham a customer can choose either a 6-month or a 12-month revolving (ongoing) payment option.
ANNEXURE A shows Dean's clothing store statement from Markham for a certain period of the year.
Use ANNEXURE A to answer the questions that follow.
2.1.1 Write down the total balance owing on Dean's account. (2)
2.1.2 Give the full date on which the current installment is due. (2)
2.1.3 State the opening balance of the 12-month revolving account option. (2)
2.1.4 Write down the price of the item that was returned. (2)
2.1.5 Determine the total amount paid using FNB electronic payments. (3)
2.1.6 The selling price of an item includes 15% VAT.
Calculate the price of the item purchased on 19 December 2018, excluding VAT. (3)
2.2 Dean, a 25-year-old male, earns a taxable income of R305 174,44. He started his first job on 1 March 2019.
Tax payable by an individual for the tax year 1 March 2019 to 29 February 2020 is indicated in TABLE 1 below.
TABLE 1: INCOME TAX RATES FOR INDIVIDUALS 2019/2020 TAX YEAR (1 MARCH 2019 TO 29 FEBRUARY 2020)
| TAX BRACKET | TAXABLE INCOME (R) | TAX RATES (R) |
| 1 | 0-195 850 | 18% of taxable income |
| 2 | 195 851-305 850 | 35 253 + 26% of taxable income above 195 850 |
| 3 | 305 851-423 300 | 63 853 + 31% of taxable income above 305 850 |
| 4 | 423 301-555 600 | 100 263 + 36% of taxable income above 423 300 |
| 5 | 550 601-708 310 | 147 891 + 39% of taxable income above 555 600 |
| 6 | 708 311-1 500 000 | 207 448 + 41% of taxable income above 708 310 |
| 7 | 1 500 001 and above | 532 041 + 45% of taxable income above 1 500 000 |
Use TABLE 1 to answer the questions that follow.
2.2.1 Name the government institution responsible for collecting tax return forms. (2)
2.2.2 Write down the tax bracket that will be used to calculate Dean's tax payable. (2)
2.2.3 Calculate the monthly tax payable by Dean before any rebates are deducted. (5)
2.2.4 TABLE 2 below indicates the rebates for the 2018/2019 and 2019/2020 tax years.
TABLE 2: REBATES FOR 2018/2019 AND 2019/2020 TAX YEARS
| TAX REBATES | TAX 2019/2020 | TAX 2018/2019 |
| Primary (age below 65) | R14 067 | R14 220 |
| Secondary (age 65 and above) | R7 713 | R7 794 |
| Tertiary (age 75 and older) | R2 574 | R2 601 |
- Identify the tax rebate(s) that Dean qualifies for in the 2019/2020 tax year. (2)
- State the number of tax rebates a 75-year-old man will qualify for in any tax year. (2)
2.3 Dean's mother, Ella, started her own instant photography business by taking photographs on the beach. She has a camera, but needs to buy a printer, photo paper and ink cartridges for printing.
TABLE 3 shows Ella's income and expenses for producing and selling up to 200 photographs.
TABLE 3: INCOME AND EXPENSES OF ELLA'S PHOTOGRAPHY BUSINESS
| NUMBER OF PHOTOGRAPHS | 0 | 25 | 50 | 80 | 100 | 125 | 150 | 170 | 200 |
| Income (rand) | 0 | 500 | 1000 | 1600 | 2000 | 2500 | 3000 | .... | 4000 |
| Expenses (rand) | 1125 | 1250 | 1375 | A | 1625 | 1750 | 1875 | 1975 | 2125 |
Use TABLE 3 above to answer the questions that follow.
2.3.1 Determine the selling price of ONE photograph. (2)
2.3.2 Write down the formula that could be used to calculate the total income received. (2)
2.3.3 The total expenses can be calculated using the following formula:
Expenses (in rand) = 1 125 + number of photographs x 5
- Write down the variable cost for taking ONE photograph. (2)
- Calculate missing value A. (3)
2.3.4 ANNEXURE B shows two graphs, X and Y, which can be used to represent the business.
Use ANNEXURE B to answer the following questions.
- Give a suitable heading for the graphs that were drawn. (2)
- State which graph (X or Y) represents the income received by the business. (2)
- Determine how many photographs must be sold to break even. (2)
[42]
QUESTION 3
3.1 Ten years ago, John bought a rectangular prism-shaped ottoman and two matching cubic-shaped ottomans'. He wants to refurbish each of them by having the side surfaces (excluding the top and bottom) repainted. He will also employ an upholsterer2 to re-cover the top of each ottoman and to attach cylindrical-shaped legs to the base of each ottoman. Each cubic-shaped ottoman will have prism-shaped ottoman will have 6 legs.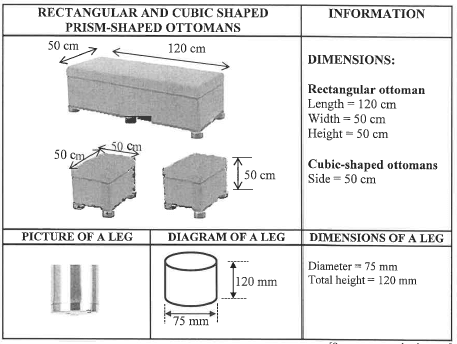
1Ottoman: a piece of furniture like a large box with a soft top, used as a seat
2Upholsterer: someone whose job it is to cover furniture with material
Use the above information to answer the questions that follow.
3.1.1 Determine the total number of legs for the ottomans John has to purchase.(3)
3.1.2 Calculate the radius of the ottoman's leg.(2)
3.1.3 Calculate, in centimetres, the total height (including the legs) of ONE cubic-shaped ottoman.(2)
3.1.4 Calculate, in cm2, the total surface area of the side surfaces of all three ottomans that need to be painted.
You may use the following formulae:
Area of a rectangle = length x width Area of a square = side x side(5)
3.1.5 John bought a one-litre tin of luxurious silk paint to paint the side surfaces. The paint has a spread rate of 8 m 2 per litre.
Calculate, in millilitres, the amount of paint needed to paint ALL the ottomans with TWO coats of paint.
3.1.6 The tin has an inner radius of 6,5 cm.
Calculate the height (in cm) of the paint in the tin, if 1 litre. = 1 000 cm3 You may use the following formula:(4)
Height = Volume
3,142 x(radius)2 (3)
3.2 The upholsterer can use the following materials to cover the tops of ALL the ottomans: synthetic leather (S), genuine leather (G) or canvas (C). The materials are available in the following colours: red (R), brown (B) and white (W).
ANNEXURE C shows a tree diagram that represents the choice and colour of the material to be used to cover the ottomans.
Use ANNEXURE C to answer the questions that follow.
3.2.1 Write down missing items (a) and (b). (4)
3.2.2 Determine (as a fraction in simplest form) the probability of NOT selecting red material. (3)
3.3 John asked the upholsterer to use synthetic leather to cover each of the ottomans. The upholsterer uses large sheets of synthetic leather, which he then cuts into smaller pieces to fit the top of each ottoman. Alibaba.com is an online store that sells the sheets of synthetic leather with a width (W) of 60 inches and a length (L) of 5 m.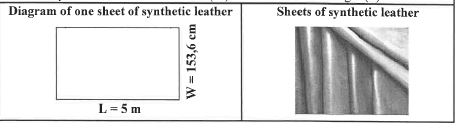
Use the above information to answer the questions that follow.
3.3.1 Given that 60 inches = 153,6 cm, complete:
1 inch = ... cm (2)
3.3.2 Calculate, in cm, the perimeter of one large sheet of synthetic leather.
You may use the following formula: Perimeter = 2 x (length + width) (3)
[31]
QUESTION 4
4.1 Peet and his friend, Roland, plan a camping trip using their motorcycles along Cape Route 62. This is a popular tourist route passing through the Western Cape and Eastern Cape provinces.
The map on ANNEXURE D shows Cape Route 62.
Use ANNEXURE D to answer the questions that follow.
4.1.1 Identify the road that must be travelled on between Tulbagh and Ceres. (2)
4.1.2 Name the type of scale shown on the map. (2)
4.1.3 Write down the general direction from Knysna to Mossel Bay. (2)
4.1.4 The total distance from Cape Town to Worcester, via Tulbagh, is 210 km.
TABLE 4 indicates the actual distances between some of the towns on Cape Route 62.
TABLE 4: ACTUAL DISTANCES BETWEEN TOWNS
| Cape Town to Paarl | 62 km |
| Paarl to Wellington | 13 km |
| Wellington to Tulbagh | A |
| Tulbagh to Worcester | 82 km |
Determine missing value A. (2)
4.1.5 Peet wants to visit his cousin, who lives along Cape Route 62.
He uses the following directions to his cousin's home:
- Peet takes the R60 from Worcester to Montagu.
- From Montagu he proceeds to Barrydale.
- From Barrydale he takes the R62 to the next town where his cousin lives.
Study the directions and then write down the name of the town where his cousin lives. (2)
4.2 Four more friends will be joining Peet and Roland. They will travel by car and use a trailer to transport their motorcycles. To protect the motorcycles from damage, they need a 20 cm space around all four sides of the motorcycles.
The dimensions of a single motorcycle are given below.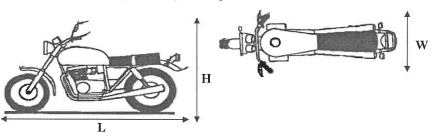
Length (L) = 229 cm, height (H) = 125 cm and width (W) = 86 cm
Below is the layout plan of the four motorcycles placed onto the trailer.
LAYOUT PLAN OF THE FOUR MOTORCYCLES ON THE TRAILER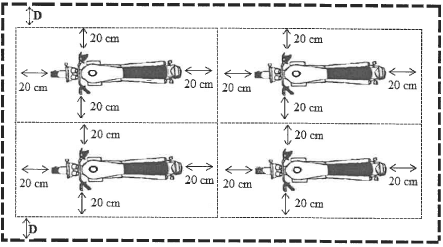
KEY: ---Outer dimensions of the trailer with a length of 550 cm and a width of 260 cm.
Use the sketches above to answer the questions that follow.
4.2.1 Calculate the minimum length required to safely place two motorcycles, one behind the other, onto the trailer, taking into account the precautionary measures above. (3)
4.2.2 If the two motorcycles are placed in the centre of the trailer, D will be the equal distance on either side of the width of the trailer, as shown in the diagram.
Calculate (in cm) the value of D. (4)
[17]
QUESTION 5
5.1 TABLE 5 below shows the results of a recent gymnastics competition held at a school. The table shows the gymnasts' names, teams, divisions and various events with total scores given to three decimal places.
TABLE 5: RESULTS OF A GYMNASTICS COMPETITION
| GYMNAST | TEAM | DIV. | EVENTS | TOTAL SCORE | |||
| VAULT | BARS | BEAM | FLOOR | ||||
| G Gilliland | GTC | Senior A | 9,550 | 9,100 | 9,400 | 9,625 | 37,675 |
| H Radebe | Olympus | Junior A | 9,450 | 9,250 | 8,900 | 9,400 | 37,000 |
| L Gumede | Olympus | Junior A | 9,475 | 9,300 | 8,700 | 9,500 | 36,975 |
| S Rigby | TGA | Senior A | 9,500 | 8,650 | 8,925 | 9,350 | 36,425 |
| H Khumalo | GTC | Senior A | 9,300 | 9,100 | A | 9,225 | 36,425 |
| C Maile | Olympus | Junior A | 8,950 | 9,050 | 9,025 | 9,375 | 36,400 |
| M Stolp | GTC | Senior A | 9,400 | 8,750 | 8,725 | 9,500 | 36,375 |
| M McBride | GTC | Junior A | 9,475 | 9,050 | 8,700 | 9,050 | 36,275 |
| A Boom | TGA | Senior A | 9,650 | 8,300 | 8,700 | 9,500 | 36,150 |
| B Makhatini | Olympus | Junior A | 9,350 | 9,200 | 9,150 | 9,350 | 37,050 |
Use TABLE 5 to answer the questions that follow.
5.1.1 Identify the team that achieved the highest score for the vault event. (2)
5.1.2 Determine the range of G Gilliland's scores. (2)
5.1.3 Calculate the mean score for the bar event. (3)
5.1.4 Determine missing value A. (3)
5.1.5 Write down the modal score for the total points scored. (2)
5.1.6 Determine, as a percentage, the probability of selecting a gymnast in the Junior division with a total score of more than 36,970. (3)
5.1.7 Calculate the value of quartile 2 for the floor event. (3)
5.2 The graph below shows the estimated total population of South Africa and the annual population growth from 2013 to 2017.
5.2.1 Write down in words, and without the use of numbers, the population of South Africa in 2013.
5.2.2 Determine, rounded to the nearest 10 000, the population increase from 2015 to 2016.
5.2.3 Calculate the annual population growth (APG) for 2015.
Use the following formula:
current population - previous population
APG = x 100%
previous population (3)
5.2.4 The ANSWER SHEET shows the bar graph for the estimated total population and annual growth from 2013 to 2017.
If the 2018 population was 57 725 606 and the population growth was 2,13%, complete the graph for 2018 on the ANSWER SHEET. (4)
[30]
TOTAL: 150
ANSWER SHEET