MATHEMATICS PAPER 1 GRADE 12 QUESTIONS - NSC EXAMS PAST PAPERS AND MEMOS NOVEMBER 2020
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2020
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTION 1
1.1 Solve for x:
1.1.1 x2 - 6x = 0 (2)
1.1.2 x2 +10x + 8 = 0 (correct to TWO decimal places) (3)
1.1.3 (1 - x)(x + 2) < 0 (3)
1.1.4 √x + 18 = x - 2 (5)
1.2 Solve simultaneously for x and y:
x + y = 3 and 2x2 + 4xy - y =15 (6)
1.3 If n is the largest integer for which n200 < 5300 ,determine the value of n. (3)
[22]
QUESTION 2
2.1 7: x ; y; -11 ; ... is an arithmetic sequence. Determine the values of x and y. (4)
2.2 Given the quadratic number pattern: -3 ; 6 ; 27; 60 ;
2.2.1 Determine the general term of the pattern in the form Tn = an 2+ bn + c (4)
2.2.2 Calculate the value of the 50th term of the pattern. (2)
2.2.3 Show that the sum of the first n first-differences of this pattern can be given by Sn = 6n2 + 3n. (3)
2.2.4 How many consecutive first-differences were added to the first term of the quadratic number pattern to obtain a term in the quadratic number pattern that has a value of 21 060? (4)
[17]
QUESTION 3
3.1 Prove that ![]() is a convergent geometric series. Show ALL your calculations.(3)
is a convergent geometric series. Show ALL your calculations.(3)
3.2 If ![]() determine the value of p.(5)
determine the value of p.(5)
[8]
QUESTION 4
4.1 Given: h(x) = -3 + 2
x - 1
4.1.1 Write down the equations of the asymptotes of h. (2)
4.1.2 Determine the equation of the axis of symmetry of h that has a negative gradient. (2)
4.1.3 Sketch the graph of h, showing the asymptotes and the intercepts with the axes. (4)
4.2 The graphs of f(x) = ½(x + 5)2 -8 and g(x) = ½x + 9/2 are sketched below.
- A is the turning point of f
- The axis of symmetry of f intersects the x-axis at E and the line g at D(m ; n).
- C is the y-intercept of f and g.
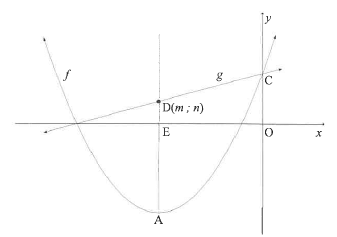
4.2.1 Write down the coordinates of A. (2)
4.2.2 Write down the range of f (1)
4.2.3 Calculate the values of m and n. (3)
4.2.4 Calculate the area of OCDE.(3)
4.2.5 Determine the equation of g-1, the inverse of g, in the form y =... (2)
4.2.6 If h(x) = g-1(x)+ k is a tangent to f determine the coordinates of the point of contact between h and f (4)
[23]
QUESTION 5
The graph of f (x) = 3-x is sketched below. A is the y-intercept of f B is the point of intersection of f and the line y = 9.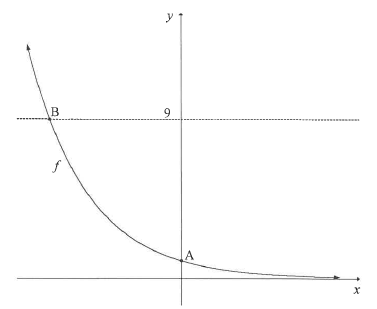
5.1 Write down the coordinates of A.(1)
5.2 Determine the coordinates of B.(3)
5.3 Write down the domain of f -1 (2)
5.4 Describe the translation from f to h(x) = 27/3x (3)
5.5 Determine the values of x for which h(x) < 1. (3)
[12]
QUESTION 6
6.1 On 31 January 2020, Tshepo made the first of his monthly deposits of R1 000 into a savings account. He continues to make monthly deposits of R1 000 at the end of each month up until 31 January 2032. The interest rate was fixed at 7,5% p.a., compounded monthly.
6.1.1 What will the investment be worth immediately after the last deposit? (4)
6.1.2 If he makes no further payments but leaves the money in the account, how much money will be in the account on 31 January 2033? (2)
6.2 Jim bought a new car for R250 000. The value of the car depreciated at a rate of 22% p.a. annually according to the reducing-balance method. After how many years will its book value be R92 537,64? (3)
6.3 Mpho is granted a loan under the following conditions:
- The interest rate is 11,3% p.a., compounded monthly.
- The period of the loan is 6 years.
- The monthly repayment on the loan is R1 500.
- Her first repayment is made one month after the loan is granted.
6.3.1 Calculate the value of the loan. (3)
6.3.2 How much interest will Mpho pay in total over the first 5 years? (4)
[16]
QUESTION 7
7.1 Determine f '(x) from first principles if f(x) = 2x2 -1 (5)
7.2 Determine:
7.2.1 d/dx(5√x2 + x3)(3)
7.2.2 f '(x) if f(x) = 4x2 - 9 ; x ≠ - 3 (4)
4x + 6 2
[12]
QUESTION 8
The graph of g (x) = ax3 + bx2 + cx, a cubic function having a y-intercept of 0, is drawn below. The x-coordinates of the turning points of g are -1 and 2.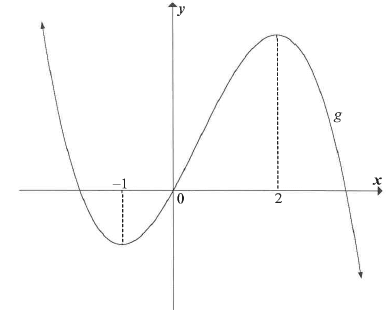
8.1 For which values of x will g increase? (2)
8.2 Write down the x-coordinate of the point of inflection of g. (2)
8.3 For which values of x will g be concave down? (2)
8.4 If g 1(x) = - 6x2 + 6x +12 , determine the equation of g. (4)
8.5 Determine the equation of the tangent to g that has the maximum gradient. Write your answer in the form y = mx + c (5)
[15]
QUESTION 9
A closed rectangular box has to be constructed as follows:
- Dimensions: length (1), width (w) and height (h).
- The length (1) of the base has to be 3 times its width (w).
- The volume has to be 5m3.
The material for the top and the bottom parts costs R15 per square metre and the material for the sides costs R6 per square metre.
9.1 Show that the cost to construct the box can be calculated by: Cost = 90w2 + 48wh (4)
9.2 Determine the width of the box such that the cost to build the box is a minimum. (6)
[10]
QUESTION 10
In a certain country, 10-digit telephone numbers with the following format were introduced:
| Format | Area Code | Exchange Code | Number |
| Number of digits | 3 digits | 3 digits | 4 digits |
| Example | 901 | 544 | 1230 |
Digits may be repeated.
10.1 How many possible 10-digit telephone numbers could be formed? (2)
10.2 Certain restrictions were placed on the groups of digits:
- Area code: must be 3 digits and the first digit can NOT be 0 or 1
- Exchange code: must be 3 digits and the first and second digits can NOT be 0 or 1
- Number: must be 4 digits and the first digit MUST be a 0 or 1
10.2.1 How many valid 10-digit telephone numbers could be formed by applying the given restrictions? (3)
10.2.2 Determine the probability that any randomly chosen 10-digit telephone number would be a valid phone number. (2)
[7]
QUESTION 11
Harry shoots arrows at a target board. He has a 50% chance of hitting the bull's eye on each shot.
11.1 Calculate the probability that Harry will hit the bull's eye in his first shot and his second shot.(2)
11.2 Calculate the probability that Harry will hit the bull's eye at least twice in his first three shots.(3)
11.3 Glenda also has a 50% chance of hitting the bull's eye on each shot. Harry and Glenda will take turns to shoot an arrow and the first person to hit the bull's eye will be the winner. Calculate the probability that the person who shoots first will be the winner of the challenge. (3)
[8]
TOTAL:150
INFORMATION SHEET
