TECHNICAL MATHEMATICS PAPER 2
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2020

INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of 11 questions.
2. Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
3. Clearly show ALL calculations, diagrams, graphs, etc. that you have used to determine your answers.
4. Answers only will NOT necessarily be awarded full marks.
5. If necessary, round off answers to TWO decimal places, unless stated otherwise.
6. Diagrams are NOT necessarily drawn to scale.
7. You  may   use   an  approved   scientific   calculator (non-programmable  and non-graphical), unless stated otherwise.
8. An information sheet with formulae is included at the end of the question paper.
9. Write neatly and legibly.

QUESTION 1
The picture below shows the triangular rooftop of a building. The diagram next to the picture represents the triangular rooftop in the Cartesian plane with origin O.
In the diagram,  A(-2 ; -1), B(-4; k)  and  C(2 ; 1)    are the vertices of ΔABC  with M(-1 ; 2) the midpoint of BC.
The angle of inclination, θ , is the angle between AC and the positive x-axis.

1.1 Determine:
1.1.1 The numerical value of k  (2)
1.1.2 The gradient of AC  (2)
1.1.3 The size of θ (in degrees) (2)
1.1.4  The equation of straight line BC in the form y = ....(3)
1.2   If O is the midpoint of AC, use analytical geometry methods to show that:
1.2.1 MO II BA
1.2.2 MO = ½ BA

QUESTION 2
2.1 The diagram below shows a circle with centre θ at the origin.
Point T(-3 ; 4) lies on the circle. Tangent RT to the circle passes through T.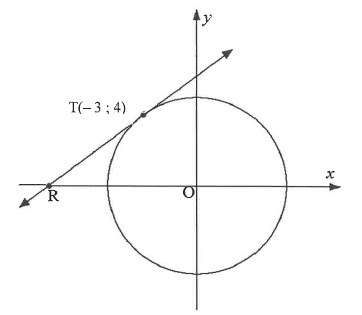

2.1.1  Calculate the length of the diameter of the circle. (2)
2.1.2 Prove, showing ALL calculations, that the straight line defined by the equation 4y - 3x - 25 = 0 and which passes through point T is the tangent to the circle. (5)
2.2 Given the ellipse with the following properties:

• Centre at the origin
• Distance between the x-intercepts is 12 units
• Range of -3,5 ≤ y ≤ 3,5

2.2.1  Write the equation of the ellipse in the form  x ² +  y ²  (1)
                                                                                a²      b²
2.2.2 Sketch the graph of the ellipse. Clearly show the intercepts with the axes. (3)
[11]

QUESTION 3
3.1  If P = 146,31° and Q = 91,58°, determine the value of  √         2         (2)
                                                                                                 tan(P + Q)
3.2 Given: tan β = -²/₃ where cos β > 0 and sinθ = ⁵/₃ where θ ∈ [90° ; 360°]
Determine, with the aid of diagrams and WITHOUT using a calculator, the value of EACH of the following:
3.2.1 2 cotβ + 1(2)
3.2.2 sin β • sec θ(6)
3.3 Given:  sin A+ 2 cos² A= 2
3.3.1 Express the above equation in simplified form, in terms of sin A.(3)
3.3.2 Hence, or otherwise, determine the value(s) of A if:
sin A + 2cos²A = 2 for A ∈ [0°; 180°)

QUESTION 4
4.1 Simplify EACH of the following:
4.1.1 1 - cos2(2π -θ) (2)
4.1.2  cos a (cot a + tan a) (4)
4.2 Prove the following identity:
                  1                    - cot² (180°- x) = 1
sin(180°+ x)•sin(360°- x)

QUESTION 5
Given: Functions f and g defined by f (x) = - tan x and g (x) = 2 sin x for  0°≤ x ≤ 180°
5.1 Draw sketch graphs of f and g on the same set of axes. Clearly indicate ALL the intercepts with the axes, turning points, asymptotes and end points. (6)
5.2 Write down:
5.2.1 The range of f  (1)
5.2.2 The period of g (1)
5.2.3 The equation of the asymptote of h if h(x) = f (x + 30°) (1)
5.3 Determine the value(s) of x for which f(x) • g(x) < 0 (2)
[11]

QUESTION 6
The picture below shows two vertical rectangular walls that are not perpendicular to each other. The diagram next to it represents the two rectangular walls, ABCF and CDEF.
Points A, F and E lie in the same horizontal plane and form a triangular section AFE of the floor.
Furthermore, FAC = 42° , FE = 4,5 m and CF= ²/₃FE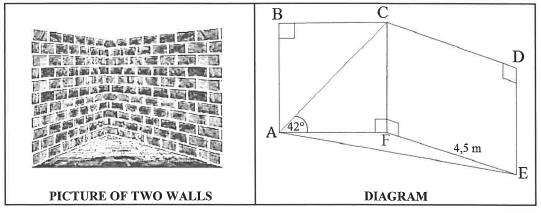

6.1 Write down the length of CF.
6.2 Determine, correct to ONE decimal place:
6.2.1 The length of AF
6.2.2 The size of AFE if AE = 6 m
6.2.3 The area of ΔAFE
[10]

QUESTION 7
7.1 Complete the following theorem:
Angles subtended by a chord of a circle, ... , are equal. (1)
7.2 In the diagram below, O is the centre of circle KLMNP.
KOM is a diameter of the circle and chords LP and PM are drawn.
N = 128°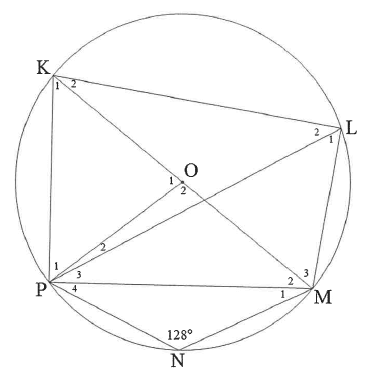

Determine, stating reasons, the size of EACH of the following angles:
7.2.1 K₁
7.2.2 L₂
7.2.3 P₂ if P₃ = 29°
[10]

QUESTION 8
8.1 Complete the following theorem:
The angle between the tangent to a circle and the chord drawn from the point of contact is equal to ... (1)
8.2 In the diagram below, TVW is the tangent to circle PRVQ at V.
Chords PV and QR intersect at point S.
TW II QR
P =42°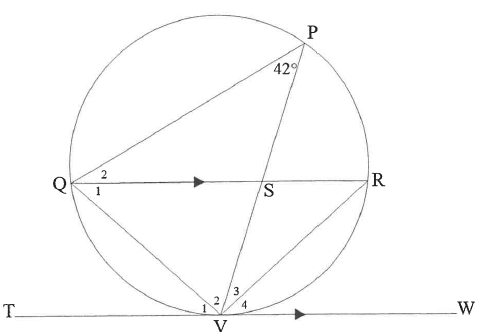

Determine, with reasons:
8.2.1 FOUR other angles each equal to 42°
8.2.2 Whether QR is a diameter of the circle
8.2.3 The size of Q₂  if V₂ = 67°
[12]

QUESTION 9
9.1 Complete the following theorem:
The perpendicular bisector of a chord of a circle passes through ...(1)
9.2 In the diagram below, O is the centre of circle  ABC  and  D  is the centre of circle ACE.
AB and AC are the diameters of the larger and smaller circles respectively.
BC is the tangent of the smaller circle at C.
DO = 6 units and AC = 8 units.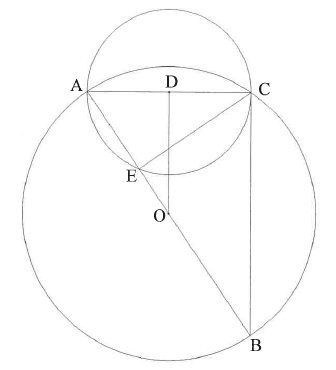

9.2.1 Give TWO different reasons why ACB = 90°(2)
9.2.2 Give a reason why DO II CB. (1)
9.2.3 Determine the length of diameter AB.(4)
9.2.4 Prove that ΔABC III ΔACE. (3)
9.2.5 Show that AC² = AB x AE (1)
9.2.6 Determine the length of AE. Leave your answer in simplified surd form. (3)
[15]

QUESTION 10
10.1 The picture below shows a spanner being used to tighten a bolt by rotating it in a clockwise direction from point  A to point B. The diagram next to the picture represents the rotation of the spanner. Point O,  the centre of the bolt, is also the centre of rotation of the spanner.
OA represents the distance from the centre of the bolt to the end of the spanner.
Reflex angle AOB = ²⁹/₁₈π and OC ⊥ BA.
Arc length of AB is 7π  cm.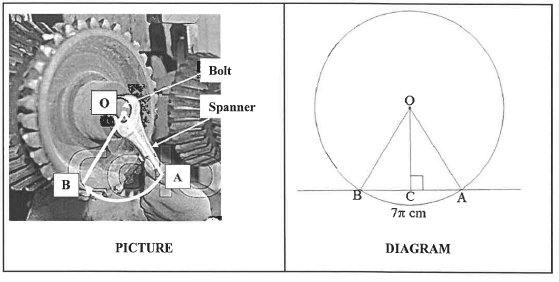

10.1.1 Write down, in radians, the size of acute AOB(1)
10.1.2 Hence, convert the size of acute  AOB to degrees.
10.1.3 Determine the length of OA.
10.1.4 Calculate the area of major sector AOB.
10.2 The picture below shows a wind turbine that is used to harness the power of wind to produce electricity.
The diagram below represents the rotating blades. The tips of the blades form a circular path when rotated. The smaller circle represents the generator.
The three identical rotating blades each have a length of 4,95 m (from point F to the tip of the blade).
KE = 10,5 m  is a chord of the larger circle and is also a tangent to the smaller circle at point F.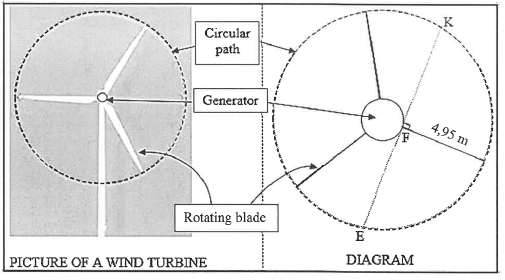

Calculate:
10.2.1 The length of the diameter of the circular path formed by the tips of the rotating blades
10.2.2 The number of revolutions per minute if the circumferential velocity of the tip of a rotating blade is 6,61π metres per second(4)
[16]

QUESTION 11
11.1 The picture below shows a partially painted rectangular wall which has a breadth of 4 m.
The diagram below represents the situation above.
The height of the unpainted part of the wall is divided into four equal parts that are each 1,5 m long, as shown in the diagram.
The ordinates of the parts are:
1,5 m;  2,1 m;  2,4 m;  2,8 m and    2,7 m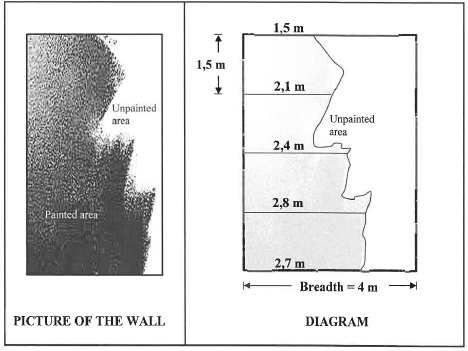

The following formula may be used:
Area of a rectangle = length x breadth
11.1.1 Determine the height of the wall. (1)
11.1.2 Calculate the painted area of the wall by using the mid-ordinate rule. (4)
11.1.3 A one-litre tin of paint, which is sufficient to cover an area of 3,26 m², costs R156,36.
Determine whether the minimum cost of the paint required to paint the remaining section of the wall will exceed R600.
NOTE: The paint is only sold in one-litre tins.(6)
11.2 The picture below shows a truck used for transporting liquid in a tank. The shape of the tank consists of a right cylindrical section in the middle with hemispheres at each end.
The diagram below shows the side view of the tank which is 6 m long.
The cylindrical section of the tank is 3 m long and the length of the radius of both the cylindrical and hemispherical sections of the tank is equal to 1,5 m.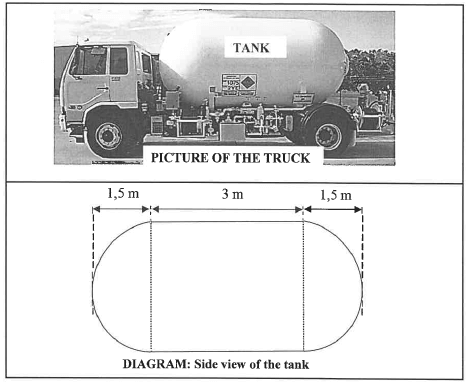

The following formulae may be used:
Total surface area of a right cylinder = 2πr² + 2πrh
Area of a rectangle = length x breadth
Volume of a right cylinder = (π²) x height
Surface area of a sphere = 4πr²
Volume of a sphere = ⁴/₃ πr²
11.2.1 Calculate the total surface area of the tank. (5)
11.2.2 A right cylindrical tank has the same volume and the same radius as the tank of the truck. Show whether the height of this right cylindrical tank is more than three times its radius.(5)
[21]
TOTAL:150

INFORMATION SHEET: TECHNICAL MATHEMATICS