Physical Sciences Paper 1 Questions - Grade 12 June 2021 Exemplars
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupINSTRUCTIONS AND INFORMATION
- This question paper consists of 10 questions.
- Answer ALL the questions.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Number the questions correctly according to the numbering system used in this question paper.
- You are advised to use the attached DATA SHEETS.
- The formulae and substitutions must be shown in ALL calculations.
- Give brief motivations, discussions, etc. where required.
- Round off your final numerical answers to a minimum of TWO decimal places.
- Start EACH question on a NEW page.
- All diagrams are not necessarily drawn according to scale.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Four possible options are provided as answers to the following questions. Choose the answer and write down (A–D) next to the question numbers (1.1–1.10) in your ANSWER BOOK, for example 1.11 D.
1.1 Safety belts in cars are designed to reduce the extent of injuries to passengers during accidents. Which ONE of Newton’s laws of motion best explains the tendency of a passenger’s body to move forward during a head-on collision?
- Law of Universal gravitation
- First Law
- Second Law
- Third Law (2)
1.2 An object of mass m rests on a flat table. If the action force of the Earth on this object is mg, which ONE of the statements given below best describes the reaction force?
- The table pushing up on the object with force mg
- The object pushing down on the table with force mg
- The object pulling upward on the Earth with force mg
- The table pushing down on the floor with force mg (2)
1.3 A constant net force, F, acts on a box which moves along a frictionless horizontal surface. Which ONE of the following quantities remains constant while the net force F acts on the box?
- Change in momentum
- Work done on the box
- Rate of change of velocity
- Change in gravitational potential energy (2)
1.4 A ball is dropped from a hot air balloon that is moving upwards at a constant velocity. Take UPWARDS as the POSITIVE direction. The correct velocity versus time graph for the motion of the ball and the balloon is: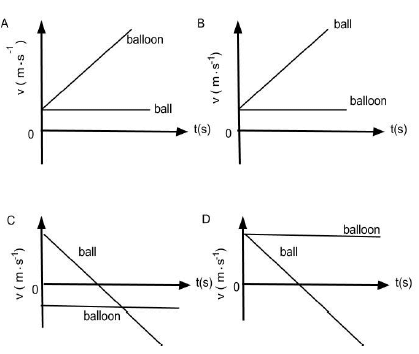 (2)
(2)
1.5 Two forces, each of magnitude 200 N, are simultaneously applied to a toolbox of mass 25 kg resting on a horizontal surface as shown in the diagram below. Ignore the effects of friction.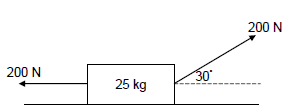
Work will be done by the net force on the toolbox because it will …
- accelerate to the left.
- accelerate to the right.
- be lifted off the surface.
- remain at rest. (2)
1.6 While a helicopter is moving vertically upwards with constant velocity, a camera is dropped from it. The camera lands on the ground after t1 seconds. The sketch graph below represents the velocity-time relationship of the camera’s motion. Downward direction is positive.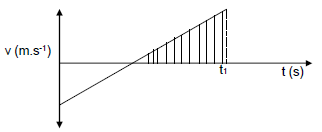
The shaded area under the graph represents the:
- Total distance the camera has travelled
- Speed with which the camera strikes the ground below
- Maximum height of the camera above the ground
- Magnitude of the displacement of the camera (2)
1.7 The work done by the car’s engine to increase its velocity from 0 to v is W. What work should be done by the engine to increase its velocity from v to 2v ?
- 4W
- 3W
- 2W
- W (2)
1.8 An ambulance moving at constant velocity, producing a sound, approaches a stationary listener, passes the listener and moves away. Which ONE of the following graphs best represents the change in observed frequency versus time?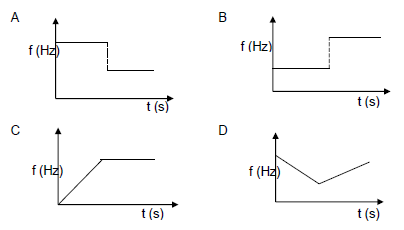 (2)
(2)
1.9 Two identical metal spheres, each carrying a charge Q, are at a distance r apart. Which ONE of the following pairs of changes, that are made simultaneously, will DOUBLE the electrostatic force that one charged sphere exerts on the other?
DISTANCE BETWEEN CENTRES OF SPHERES | MAGNITUDE OF CHARGES | |
A | Decrease distance to r | Reduce the charges on both spheres to Q |
B | Decrease distance to r | Double the charges on both spheres |
C | Decrease distance to r | Double the charges on both spheres |
D | Decrease distance to r | Reduce the charge on one sphere to Q |
(2)
1.10 Two objects experience an INELASTIC collision in an isolated system. Which ONE of the following combinations regarding the total momentum and total kinetic energy is correct?
Total momentum is … | Total kinetic energy is … | |
A | not conserved | conserved |
B | conserved | not conserved |
C | not conserved | not conserved |
D | conserved | conserved |
(2)
[20]
QUESTION 2 (Start on a NEW page.)
Two blocks, A and B, are placed on an inclined rough surface that makes an angle of 35° with the horizontal. Nceba is applying a force F on block A to push the system up the incline. Block B experiences a frictional force of 15 N.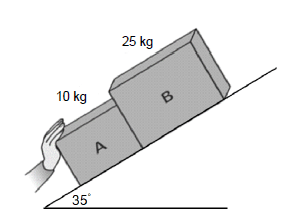
2.1 State Newton’s Third law of motion in words. (2)
2.2 Draw a labelled free-body diagram of all the forces acting on block B. (4)
2.3 If the system accelerates at 1,5 m.s-2 up the incline, calculate the force exerted by block B on block A. (6)
2.4 If block A experiences a frictional force of 4,5 N when the system was accelerating at 1,5 m.s-2, calculate the magnitude of the force applied by Nceba. (4)
[16]
QUESTION 3 (Start on a NEW page.)
Two boxes of mass m and 15 kg, are connected by a light inextensible string passing over a frictionless pulley. A force of 500 N is applied, at an angle of 40° to the horizontal, on the box of mass m as shown in the diagram below. The box of mass m experiences a frictional force of 115 N and a normal force, FN, of 623,3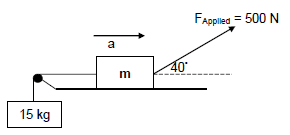
3.1 State Newton’s Second Law of motion in words. (2)
3.2 Calculate the value of m in the diagram above. (5)
3.3 Calculate the magnitude of the acceleration of the system as it moves towards the direction indicated on the diagram. (7)
[14]
QUESTION 4 (Start on a NEW page.)
Two balls A and B, are thrown simultaneously from different positions of the balcony overlooking the street. Ball A is thrown vertically upwards with a velocity of 5 m·s-1 from the top of a balcony and ball B is thrown vertically upwards with a velocity of 8 m.s-1 from the bottom of the balcony. Ignore effects of air resistance.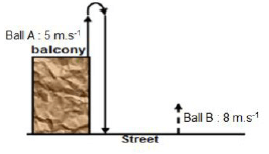
4.1 Define the term projectile. (2)
4.2 Calculate the magnitude of the displacement above the balcony of ball A. (3)
4.3 If the height of the balcony is 5 m, show by calculations whether or not ball B reached the maximum height reached by ball A. (5)
4.4 Calculate the speed at which ball B was moving when ball A reached its maximum height. (4)
4.5 At what time (in minutes) will the speed of the two balls be equal? (5)
[19]
QUESTION 5 (Start on a NEW page.)
A car of mass 1 140 kg, moving towards the east with a velocity of 30 m.s-1, collides with an oncoming delivery van of mass 1 650 kg. After collision, the van continues moving towards its original direction at 12 m.s-1 whilst the car moves at 10 m.s-1. The system is isolated.
5.1 What is meant by isolated system? (2)
5.2 Determine the magnitude of the initial momentum of the car. (3)
5.3 Calculate the velocity of the van before collision. (5)
5.4 Name and state the principle used to answer QUESTION 5.3. (3)
5.5 Calculate the change in momentum of the van. (3)
[16]
QUESTION 6 (Start on a NEW page.)
A car with a mass of 1 125 kg travelling at a constant velocity of 25 m.s-1 collided with a tree and rebounds with a velocity of 6 m.s-1.
The car was in contact with the tree for 3,5 s.
6.1 State Newton’s Second Law of motion in terms of momentum in words. (2)
6.2 Calculate the total initial kinetic energy of the system. (4)
6.3 Calculate the impulse of the tree during the collision. (4)
6.4 Calculate the average force experienced by the car. (3)
6.5 Discuss by using the principles of physics, how the airbags of the car reduce the extent of injuries suffered by the driver. (2)
6.6 If the car did not rebound from the tree but the time interval remained 3,5 s, how will the magnitude of the force exerted on the car be influenced? Write only INCREASE, DECREASE or REMAIN THE SAME. Explain the answer. (4)
[19]
QUESTION 7 (Start on a NEW page.)
A research satellite has a mass of 3,4 x 103 kg. It orbits the Earth at a distance of 2,32 x 106 m from the centre of the Earth, which has a mass of 5,98 x 1024 kg.
7.1 Calculate the gravitational force that the Earth exerts on the satellite. (4)
7.2 Name and state the law that is applicable to this situation. (3)
7.3 Another satellite of mass half that of the research satellite orbits at a distance half that of the research satellite from the centre of the Earth. Calculate the magnitude of the force of attraction between the Earth and this satellite. (3)
[10]
QUESTION 8 (Start on a NEW page.)
8.1 A crate of mass 8 kg was resting at point A on an inclined rough surface that makes an angle of 30° with the horizontal. Two forces F1 and F2, of 20 N and 100 N respectively, were simultaneously applied on the crate and it moved through a displacement of 20 m, as shown in the diagram below.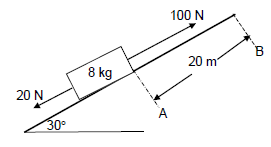
8.1.1 State the work-energy theorem in words. (2)
8.1.2 If the frictional force experienced by the crate is 8,5 N, calculate the net work done in moving the crate to point B. (4)
8.1.3 Use energy principles to calculate the velocity of the box as it passes point B. (4)
8.2 A race car with a mass of 1 500 kg can reach a speed of 26 m.s-1 from 0 m.s-1 in 4 s. Calculate the average power output of the car’s engine. (5)
[15]
QUESTION 9 (Start on a NEW page.)
9.1 A hospital staff member moves away from an ambulance. The siren of the ambulance produces a sound of an unkown frequency. The staff member hears 0,85 times the frequency of the siren as he moves away from the ambulance. The speed of sound in the air is 340 m.s-1.
9.1.1 Define Doppler effect. (2)
9.1.2 Calculate the velocity of the staff member as he moves away from the ambulance. (4)
9.1.3 Why is the frequency perceived by the listener moving away from the source lower than the actual frequency produced by the siren? (2)
9.1.4 If the staff member decided to get inside the ambulance, how would the frequency heard by the staff member compare, to that emitted by the ambulance? Write only GREATER THAN, SMALLER THAN or EQUAL TO. (2)
9.1.5 If the frequency of the source was 190 Hz, what will be the magnitude of the frequency registered by the staff member as he was moving away from the ambulance? (2)
9.2 Name TWO applications of the Doppler effect in Medical Science. (2)
[14]
QUESTION 10 (Start on a NEW page.)
The diagram below shows three point charges, A carrying a charge of -4 nC, B carrying a charge of +8 nC and N carrying a charge of +2 nC. These point charges are placed at distance apart from one another as shown in the diagram below.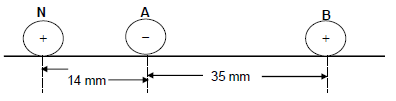
10.1 State Coulomb’s law in words. (2)
10.2 Calculate the magnitude and direction of the net force around point charge N due to the presence of both point charges A and B. (5)
[7]
TOTAL: 150
DATA FOR PHYSICAL SCIENCES GRADE 12
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Acceleration due to gravity | g | 9,8 m•s-2 |
Universal gravitational constant | G | 6,67 × 10-11 N•m2•kg-2 |
Speed of light in a vacuum | c | 3,0 × 108 m•s-1 |
Planck's constant | h | 6,63 × 10-34 J•s |
Coulomb's constant | k | 9,0 × 109 N•m2•C-2 |
Charge on electron | e | -1,6 × 10-19 C |
Electron mass | me | 9,11 × 10-31 kg |
Mass of earth | M | 5,98 × 1024 kg |
Radius of earth | RE | 6,38 × 103 km |
TABLE 2: FORMULAE
MOTION
| vf = vi + aΔt | Δx = ViΔt + ½aΔt2 or Δy = ViΔt2 + ½aΔt2 |
Vf2 = Vi2 + 2aΔx or Vf2 = vi2 + 2aΔy | Δx = [Vi + Vf]Δt or Δy = [Vi + Vf]Δt |
FORCE
Fnet = ma | p= mv |
fsmax = µsN | fk = µkN |
FnetΔt = Δp | w =mg |
F = Gm1m2 | g = G M |
WORK, ENERGY AND POWER
W =FΔxcosθ | U= mgh or EP = mgh |
K = ½mv2 or Ek = ½mv2 | Wnet = ΔK or Wnet = ΔEk ΔK = Kf −Ki or ΔEk =Ekf − Eki |
Wnc= ΔK + ΔU or Wnc= ΔEk + ΔEp | P = W Δt |
Pav = Fv |
WAVES, SOUND AND LIGHT
v = f λ | T =1/f |
fl = v ± vl fs fl = v ± vl fb | E = hf or E = h c |
E = W0 + Ek where | |
ELECTROSTATICS
| F = kQ1Q2 r2 | E = KQ |
E = V | E = F |
V = W | n = Q |
ELECTRIC CIRCUITS
R = V | emf (ε) = I(R + r) |
RS = R1 + R2 + ....... | q = I Δt |
W = Vq | P= W |
ALTERNATING CURRENT
I rms = Imax | Paverage = VrmsIrms |