Physical Sciences Paper 1 Memorandum - Grade 12 June 2021 Exemplars
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMEMORANDUM
QUESTION 1
1.1 B √√ (2)
1.2 C √√ (2)
1.3 C √√ (2)
1.4 D √√ (2)
1.5 A √√ (2)
1.6 C √√ (2)
1.7 B √√ (2)
1.8 A √√ (2)
1.9 D √√ (2)
1.10 B √√ (2) [20]
QUESTION 2
2.1 When object A exerts a force on object B, √ object B simultaneously exerts an oppositely directed force of the same magnitude on object A. √ (2)
2.2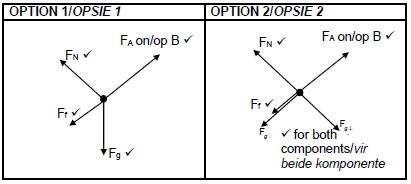 (4)
(4)
2.3 Data:
- MB = 25 kg
fB = 15 N
a = 1,5 m.s-2
FA on B = ?
FB on A = ?
Fnet = ma
FA on B + fB + Fg = ma √ Any one
FA on B + fB + mgSin35°= ma
FA on B + (- 15) + (- 25x9,8x0,574) √ = 25x1,5 √
FA on B – 155,63 = 37,50 FA on B = 193,13 N √
FB on A = - FA on B
FB on A = - 193,13 N
FB on A = 193,13 N √ down the slope √ (6)
2.4
- Fnet = ma
FNceba + FB on A + fA + Fg = ma √ Any one
FNceba + FB on A + fA + mgSin35°= ma
FNceba + (- 193,13) + (- 4,5) + (- 10x9,8x0,574) √ = 10x1,5 √
FNceba – 253,88 = 15
FNceba = 268,88 N √ (4)
[16]
QUESTION 3
3.1 When a net/resultant force acts on an object of mass m, the object accelerates in the direction of the net force. √ The accelereation is directly proportional to the net force and inversely proportional to the mass. √ (2)
3.2
- Fnet = ma
Fg + FN + FY = ma √ Any one
Fg + FN + Fa Sin40° = ma
Fg + (-623,3) + (-500Sin40°) = mx0 √
Fg - 623,3 – 321,39 = 0
Fg = 944,69 N
mg = 944,69 √
mx9,8 = 944,69 √
m = 96,40 kg √ (5)
3.3 For 96,4 kg box
- Fnet = ma
Fa Cos40° + f + T = ma
500 Cos40° + (-115) +(- T) √ = 96,4a √
383,02 – 115 – T = 96,4a
268,02 - T = 96,4a
T = 268,02 – 96,4a (1)
For 15 kg box
- Fnet = ma √ Any one
mg + T = ma
-15x9,8 + T√ = 15a √
-147 + T = 15a (Substitute)
-147 + (268,02 – 96,4a) = 15a
121,02 = 111,40a
a = 1,09 m.s-2 √ (7)
[14]
QUESTION 4
4.1 It (projectile) is an object upon which the only force acting is the force of gravity. √√
OR/OF
Projectile is an object that experiences only gravitational force. √√ (2)
4.2
OPTION 1 | |
(upwards positive) | (downwards positive) |
vf2 = vi2 + 2gΔy | vf2 = vi2 + 2gΔy |
OPTION 2 | |
(upwards positive) | (downwards positive) |
vf = vi + g∆t | vf = vi + g∆t |
(3)
4.3 The maximum height reached by ball A (Δymax) = 1,28 + 5 = 6,28 m
Maximum height reached by ball B is given by:
(upwards positive) | (downwards positive) |
vf2 = vi2 + 2gΔy 02 = 82 + 2 (-9,8) Δy ΔyB = 3,27 m Since ΔyB < Δymax OR 3,27 m < 6,28 m ∴ Ball B did not reach the maximum height. ü | vf2 = vi2 + 2gΔy 02 = (-8)2 + 2 (9,8) Δy Δy = -3,27 m ΔyB = 3,27 m, (upward) Since ΔyB < Δymax OR 3,27 m < 6,28 m ∴ Ball B did not reach the maximum height. |
(5)
4.4
(upwards positive) | (downwards positive) |
vf = vi + g∆t | vf = vi + g∆t 0 = (5) + (-9,8 ). ∆t vf = vi + g∆t |
(4)
4.5 (Upwards positive)
For ball A
vf = vi + g∆t √
vf = (5) + (-9,8 ). ∆t (1) √
For ball B
vf = vi + g∆t
vf = (8) + (-9,8 ). ∆t (2) √
Equating (1) and (2)/ Stel (1) gelyk aan (2):
Since ball A will be moving downwards then:
-(5 – 9,8.∆t) = 8 – 9,8.∆t √
19,6.∆t = 13
∆t = 0,66 s
∆t = 0,011min √ (5)
[19]
QUESTION 5
5.1 A system on which the net external forces acting is zero. √√ (2)
5.2 Let east be positive
- p = mv √
= 1 140 x 30 √
= 34 200 kg.m.s-1, (east) √ (3)
5.3
- Σpi = Σpf √
mvviv + mcvic = mvvfv +mcvfc
1 650 viv+ 1 140 x 30 √ = 1 650 x - 12 + 1 140x 10 √
1 650 viv = 11 400 – 34 200 – 19 800 viv = - 25,82
viv = 25,82 m.s-1 √, west √ (5)
5.4 Principle of conservation of linear momentum √
The total linear momentum of an isolated system remains constant (preserved). √√ (3)
5.5
- ∆p = m(vf - vi) √
∆p = 1 650 (-12 – (-25,82)) √
∆p = 22 803 kg.m.s-1 √ (3)
[16]
QUESTION 6
6.1 The net/resultant force acting on an object is equal to the rate of change in momentum of the object. √√ (2)
6.2
- Total Ek Before = Ek tree + Ek car
= ½m v2tree + ½m
= ½(m)(02) √ + ½(1 125)(25)2 √
= 351 562,5 J √ (4)
6.3 Impulse of the tree:
Let original direction be positive
- Fnet∆t (car) = m(vf - vi) √
= 1 125(-6 – 25) √
= - 34 875 N
Fnet∆t (car) = 34 875 N, backwards/terugwaarts
Fnet∆t (tree) = 34 875 N √, original direction of the car √ (4)
6.4
- Fnet (car) = m(vf - vi ) √
Δt
Fnet (car) = 1 125(-6 - 25) √
3,5
Fnet (car) = - 9 964 N
Fnet (car) = 9 964 N, backwards √ (3)
6.5 When the airbags deploy during collision, the contact time of the driver with the airbag increases. √ According to the equation Fnet∆t = ∆p, when contact time increases the net force experienced by the driver decreases. √ Then, the extent of injury is reduced. (2)
6.6 Decrease √
The final velocity will now be zero. √ Then, according to the equation:
∆p = m(vf – vi), it follows that ∆p will decrease. √ If ∆p decreases then Fnet decreases as they are directly proportional to each other. (4)
[19]
QUESTION 7
7.1
- F = Gm1m2 √
r2
F = (6,67 x10-11)( 3,4 x103 )( 5,98 x1024 ) √
(2,32 x106 )2 √
= 251 959,05
= 2,52 x 105 N √ (4)
7.2 Newton’s Law of Universal Gravitation √
Any two objects or particles in the universe attract each other with a force which is directly proportional to the product of their masses √ and inversely proportional to the square of the distance between their centres. √ (3)
7.3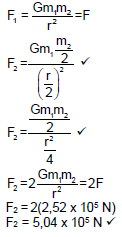 (3)
(3)
[10]
QUESTION 8
8.1
8.1.1 The net work done on an object is equal √ to the change in the kinetic energy of the object. √
OR
The amount of work done by a net force √ on an object is equal to the change in the object’s kinetic energy. √ (2)
8.1.2
OPTION 1 |
Wnet = WF1 + WF2 + W// + Wf |
OPTION 2 |
Fnet = F2 + F1 + Fg + f |
(4)
8.1.3 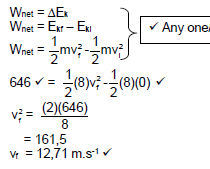 (4)
(4)
8.2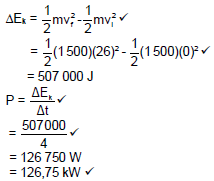 (5)
(5)
[15]
QUESTION 9
9.1
9.1.1 It is the apparent change in frequency (or pitch/wavelength) of the sound detected by a listener because the sound source and the listener have different velocities relative to the medium of sound propagation. √√
OR
An apparent change in observed/detected frequency (pitch/ wavelength) as a result of relative motion between a source and an observer. √√ (2)
9.1.2 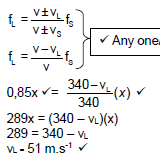 (4)
(4)
9.1.3 When the listener moves away from the source the sound waves that reach him have longer wavelength √ and a sound with a lower pitch is registered because of a lower frequency. √ (2)
9.1.4 It would be the same √√ (2)
9.1.5
- FL = 0,85fS
= 0,85 x 190 √
= 161,5 Hz √ (2)
9.2 To measure the velocity of blood flowing through blood vessels. √
To scan a fetus/foetus. √ (2)
[14]
QUESTION 10
10.1 The magnitude of the electrostatic force exerted by one point charge (Q) on another point charge (Q) is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance (r) between them. √√ (2)
10.2 East is positive
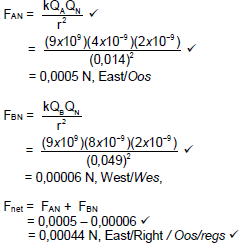 (5)
(5)
[7]
TOTAL: 150