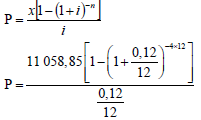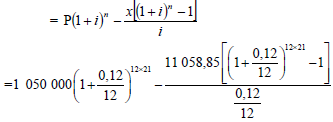MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupQUESTION 1
1.1.1
x2 - 2x - 24 = 0
(x - 6)(x + 4) = 0
x = 6 or x = -4 (3)
1.1.2
2x2 - 3x - 3 = 0
x = 3 ± √(-3)2 - 4(2)(-3)
2(2)
x = 3 ± √33
4
x = 2,19 or x = -0,69 (3)
1.1.3
x2 + 5x ≤ -4
x2 + 5x + 4 ≤ 0
(x + 4)(x + 1) ≤ 0
Critical values: x = -4 or x = -1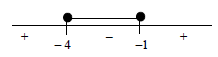 -
-
4 ≤ x ≤ -1 OR x ∈ [–4 ; –1] (4)
1.1.4
√x + 28 = 2 - x
(√x + 28)2 = (2 - x)2
x + 28 = 4 - 4x + x2
x2 - 5x - 24 = 0
(x - 8)(x + 3) = 0
x ≠ 8 or x = -3
- squaring both sides
- standard form
- factors
- answers with selection (4)
1.2
2y = 3 + x
x = 2y - 3 … (1)
2xy + 7 = x2 + 4y2 … (2)
2y(2y - 3) + 7 = (2y - 3)2 + 4y2
4y2 - 6y + 7 = 4y2 - 12y + 9 + 4y2
4y2 - 6y + 2 = 0
2y2 - 3y + 1 = 0
(2y -1)(y - 1) = 0
y = ½ or y = 1
x = -2 or x = -1
OR
2y = 3 + x
y = 3/2 + x/2 …(1)
2xy + 7 = x2 + 4y2 … (2)
2x(3/2 + x/2) + 7 = x2 + 4(3/2 + x/2)2
3x + x2 + 7 = x2 + 9 + 6x + x2
x2 + 3x + 2 = 0
(x + 2)(x + 1) = 0
x = -2 or x = -1
y = ½ or y = 1
(6)
1.3
n/m = p/n
n2 = mp
Δ = b2 - 4ac
Δ = n2 - 4mp , but n2 = mp
Δ = n2 - 4n2
Δ = - 3n2
n2 > 0
-3n2 < 0
Δ < 0 ⇒ x is a non-real number
OR
Δ = mp - 4mp
Δ = -3mp
mp > 0
-3mp < 0
(4)
[24]
QUESTION 2
2.1
90/x - 81/90
81x = 8100
x = 100 (2)
OR
x = 90 x 10/9
x = 100 (2)
2.2
Sn = a(1 - rn)
1 - r
Sn = 100(1 - (0,9)n)
1 - 0,9
Sn = 100(1 - (0,9)n)
0.1
Sn = 1 000(1 - (0,9)n) (2)
2.3
S∞ = a
1 - r
S∞ = 100
1 - 9/10
S∞ = 1000
OR
S∞ = lim [1 000(1-(0,9)n)]
S∞ = 1000
OR
substitution
answer (2)
OR
S∞ = lim [1 000(1 - (0,9)n)]
n→∞
S∞ = 1000
[6]
QUESTION 3
3.1
–82 (1)
3.2 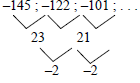
2a = -2 ∴ a = -1
3a + b = 23 ∴ 3(–1) + b = 23 ∴ b = 26
a + b + c = -145 ∴ –1 + 26 + c = –145 ∴ c= -170
∴Tn = -n2 + 26n - 170
OR
2a = -2 ∴ a = -1
c = -145 + (-2) - 23 = -170
∴Tn = -n2 + bn - 170
b = 26
∴Tn = -n2 + 26n - 170
(3)
3.3
Tn = bn + c
Tn = -2n + 25
- 2n + 25 = -121
- 2n = -146
n = 73
Between T73 and T74
or
Tn = a + (n - 1)d
= 23 + (n - 1)(-2)
= 25 - 2n
OR
Tn+1 - Tn = -(n + 1)2 + 26(n + 1) -170 - (-n2 + 26n - 170)
-121 = -2n + 25
n = 73
Between T73 and T74
3.4
n = - b = - 26 = 13
2a 2(1)
T13 = -1
∴ add 2
OR
T'n = -2n + 26 = 0
n = 13
T13 = -(13)2 + 26(13) - 170 =-1
13
∴ add 2
[11]
QUESTION 4
4.1
a = 5 and d = 2
T51 = 5 + (51 - 1)(2)
= 105
(3)
4.2
Sn = n/2[2a + (n - 1)d ]
S51 = 51/2(5) + (51 - 1)2]
= 2 805
or
S51 = 51/2[5 + 105]
= 2 805 (2)
4.3![]()
4.4
T1 = -3 T4 999 = -2(4 999) - 1 = - 9 999![]()
= (5 + 7 + 9 + … + 9 999 + 10 001 + 10 003) +(–3 – 5 – 7 – 9 – … – 9 999)
= 10 001 + 10 003 –3
= 20 001
OR
S4 999 = 4 999[2(-3) + (4 999 - 1)(-2)] = - 24 999 999
2
S5 000 = 5000((2)(5) + (5 000 - 1)(2)) = 25 020 000
2![]() = 25 020 000 – 24 999 999
= 25 020 000 – 24 999 999
= 20 001
(4)
[10]
QUESTION 5
5.1
x = 3
y = 2
5.2
x ∈ R, x ≠ 3
OR
x ∈ (-∞ ;3) ∪ (3;∞)
OR
x< 3 or x >3
5.3
0 = -1 + 2
x - 3
-2x + 6 = -1
x = 7/2
x-int (7/2;0)
5.4
y-int (0;7/3)
5.5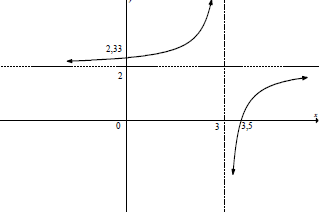
asymptotes
intercepts with the axes
shape
[10]
QUESTION 6
6.1
f (x) = log4x
2 = log4k
42 = k
∴k = 16
(2)
6.2
-1 = log4x ∴ x = ¼
¼ ≤ x ≤ 16 or x ∈ [¼; 16]
(2)
6.3
f (x) = log4x
y = log4x
x = log4y
y = 4x
(2)
6.4
x < 0
OR
x ∈ (-∞ ; 0)
[8]
QUESTION 7
7.1
B(–4 ; 0)
D(6 ; 0)
(2)
7.2
f (x) = x2 - 2x - 24
xtp = - b OR 2x - 2 = 0 OR x = -4 + 6
2a 2
x = -(-2)
2(1)
xtp = 1
ytp = f(1)
= 12 - 2(1) - 24
= -25
C(1 ; –25)
(2)
7.3
y = -25
OR
y ∈ [-25 ;∞)
(1)
7.4.1
mAE = tan14, 04º = 0, 25 = ¼
(1)
7.4.2
mtang = -4
f ' (x) = 2x - 2
2x - 2 = -4
xT = -1
yT = -21
7.5
mline = ¼
y + 9 = ¼(x + 3)
OR
-9 =¼(-3) + c
y + 9 =¼x + ¾
OR
c = 33/4 =-8, 25
y = ¼x - 33/4
OR
y = 0, 25x = -8, 25
x2 - 2x - 24 = ¼x - 33/4
4x2 - 8x = 96 = x - 33
4x2 - 9x - 63 = 0
(4x - 21)(x + 3) = 0
x = 21/4 = 5,25 or x -3
(6)
[17]
QUESTION 8
8.1
A = P(1 - i)n
A = 980 000(1 - 0, 092)7
A = R498 685,82 (3)
8.2
A = P(1 + i)n
116 253,50 = 75 000(1 + 0,068)4n
4
1,550 046 667 = (1, 017)4n
log(1,550 046 667) = 4n log(1, 017)
4n = log(1, 550 046 667) or 4n = log1,017(1,550 046 667)
log(1, 017)
4n = 25,99 …
n = 6,50 years
(4)
8.3.1
F = x [(1 + i)n - 1]
i
450 000 = 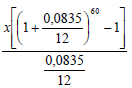
x = R6 068,69
(3)
8.3.2

P = R419 948,32
OR
Balance = A - F
=R12 887 702,20 – R12 467 749,81
=R419 952,39
(3)- Total paid =11 058,85 x 21 x 12 = 2 786 830, 20
Loan Paid = 1 050 000 - 419 948,32 = 630 051, 68
Interest paid = 2 786 830,20 – 630 051,68
= R2 156 778,52
OR
Total paid =11 058,85x 21x12 = 2 786 830, 20
Loan Paid = 1 050 000 - 419 952,39 = 630 047, 61
Interest paid = 2 786 830,20 – 630 047,61
= R2 156 782,59
OR
Interest paid
= 11 058,85 × 21 × 12 – (1 050 000 – 419 948,32)
= 2 786 830,20 – 630 051,68
= R2 156 778,52
[16]
QUESTION 9
9.1
f ' (x) = lim f (x + h) - f (x)
h→0 h
f ' (x) = lim 2(x + h)2 - 3(x + h) - (2x2 - 3x)
h→0 h
f ' (x) = lim 2x2 + 4xh + 2h2 - 3x - 3h - 2x2 + 3x
h→0 h
= lim 4xh + 2h2 - 3h
h→0 h
= lim h(4x + 2h - 3)
h→0 h
= lim(4x + 2h - 3)
h→0
f ' (x) = 4x - 3
OR
f (x) = 2x2 - 3x
f (x + h) = 2(x + h)2 - 3(x + h)
f (x + h) = 2x2 + 4xh + 2h2 - 3x - 3h
f (x + h) - f (x) = 4xh + 2h2 - 3h
f ' (x) = lim f (x + h) - f (x)
h→0 h
= lim 4xh + 2h2 - 3h
h→0 h
= lim h(4x + 2h - 3)
h→0 h
= lim(4x + 2h - 3)
h→0
∴ f ' (x) = 4x - 3
9.2.1
y = 4x5 - 6x4 + 3x
dy/dx = 20x4 - 24x3 + 3
9.2.2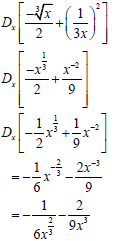
(4)
[12]
QUESTION 10
10.1
h(x) = ax3 + bx2
h ' (x) = 3ax2 + 2bx
h ' (4) = 0
48a + 8b = 0
6a + b = 0 ...(1)
h(4) = 32
64a + 16b = 32
4a + b = 2 ...(2)
(1) – (2): 6a + b = 0
4a + b = 2
2a = – 2
a = – 1
4(– 1) + b = 2
b = 6
10.2
h(x) = -x3 + 6x2
- x3 + 6x2 = 0
x2 (-x + 6) = 0
x = 0 or x = 6
∴A(6 ; 0)
(3)
10.3.1
0 < x < 4 or 0 ≤ x ≤ 4
OR
x (0 ; 4) or x [0 ; 4]
(2)
10.3.2
x > 2
OR
x (2 ; )
10.4
f (x) = h(x - 1) = -(x - 1)3 + 6(x - 1)2
f (0) = 7
7 < k < 32 or k (7 ; 32)
(3)
[15]
QUESTION 11
Time = 20/x
Cost = (water cost per hour × time) + (kms × R/km)
C(x) = 1,6 x (20/x) + 20(1,2 + x/4000)
C(x) = 32/x + 24 + x/200
C ' (x) = - 32 + 1 = 0
x2 200
x2 = 6 400
x = 80 km/ h
[7]
QUESTION 12
12.1.1
No, because P(A and B) ≠ 0 (1)
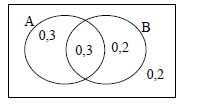
12.1.2
- P(A and B) = 0,3 P(only B) = 0,2
P(A and B) = P(A) x P(B)
0,3 = P(A) x 0,5
P(A) = 0,6
P(only A) = 0,3 (4) 
P(not A or not B) = 0, 2 + 0, 2 + 0,3 = 0, 7
OR
P(not A or not B) = 1- P(A and B) = 1 - 0,3 = 0, 7
OR
P(A/ or B/) = P(A/) + P(B/) – P(A/ and B/)
= 0,4 + 0,5 – 0,2 = 0,7
12.2.1
P(novel) = 3/12 = ¼ (1)
12.2.2
12! = 479 001 600 (2)
12.2.3
| 5 | 3! | 8! | 4 |
| (Poetry) | (Novels all together) | (Arrangements of rest of the books including the novels) | (Drama) |
(4)
P(start with poetry, end with drama AND all novels together)
= 5 x 3! x 8! x 4
12!
= 1
99
[14]
TOTAL: 150