MATHEMATICAL LITERACY P2 with Memorandum - 2024 Grade 12 June Common Exams
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupQUESTION 1.3
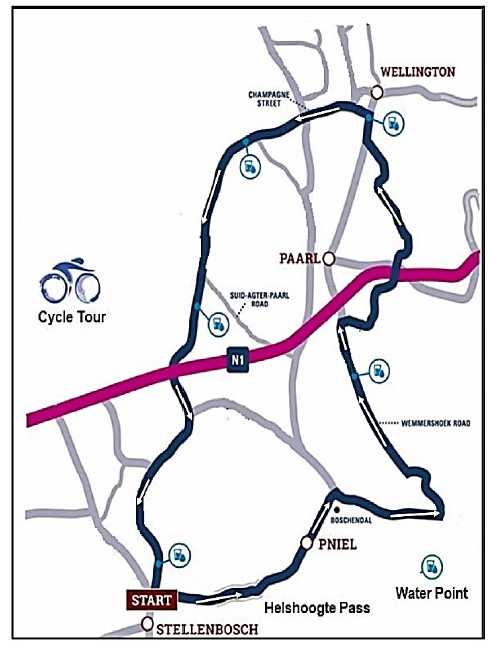
THE ROUTE MAP OF THE MEDIHELP STELLENBOSCH CYCLE TOUR
 |
QUESTION 2.2
PART OF THE MAP OF THE KRUGER NATIONAL PARK
[Adapted from https://krugernationalpark.co.za] |
TABLE 2
Distances in kilometres between some of the camps and gates in the Kruger National Park
Gates and camp distances | Berg-en-dal | Lower Sabie | Malelane | Numbi Gate | Orpen | Satara | Skukuza |
Berg-en-dal | - | 113 | 12 | 97 | 213 | 165 | 172 |
Lower Sabie | 113 | - | 105 | 95 | 141 | 93 | 43 |
Malelane | 12 | 105 | - | 94 | 204 | 156 | 64 |
Numbi Gate | 97 | 95 | 94 | - | 195 | 147 | 54 |
Orpen | 213 | 141 | 204 | 195 | - | 48 | 137 |
Satara | 165 | 93 | 156 | 147 | 48 | - | 84 |
Skukuza | 172 | 43 | 64 | 54 | 137 | 84 | - |
MARKS: 100
TIME: 2 hours
INSTRUCTIONS AND INFORMATION
- Read the following instructions carefully before answering the questions.
- This question paper consists of FOUR questions. Answer ALL the questions.
- Use the ANNEXURES in the ADDENDUM to answer the following questions:
- ANNEXURE A for QUESTION 1.3
- ANNEXURE B for QUESTION 2.2
- Number the answers correctly according to the numbering system used in this question paper.
- Start EACH question on a NEW page.
- You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
- Show ALL calculations clearly.
- Round off ALL final answers appropriately according to the given context, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Maps and diagrams are NOT necessarily drawn to scale, unless stated otherwise. 10. Write neatly and legibly.
QUESTION 1
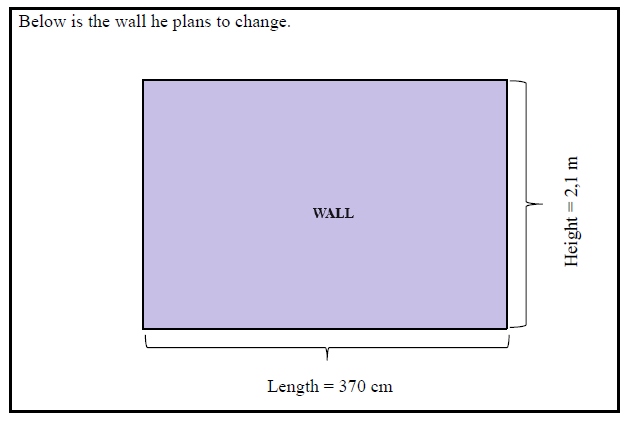
1.1 Uncle James bought a house and decided to do some renovations to the lounge area. He plans to change one of the walls in this room.
Use the information above to answer the questions that follow.
1.1.1 Define the term perimeter. (2)
1.1.2 Convert the length of the wall to metres. (2)
1.1.3 Calculate the perimeter of the wall.
You may use the following formula:
P = length + length + height + height (2)
1.2
Jameson will win a club cycling trophy if he is able to log at least 600 km of cycling distance in a seven-month period. He cycles as follows:
NOTE: 1 km = 0,6214 miles |
1.2.1 Calculate, in km, the distance he cycled in the Vineyard Race. (2)
1.2.2 Hence, determine the total distance logged by Jameson throughout the period. Give your answer in kilometre (km). (2)
1.3
| The route map of the Medihelp Stellenbosch Cycle tour is shown in ANNEXURE A. |
Use ANNEXURE A to answer the questions that follow.
1.3.1 Name ONE town that is situated directly on the route. (2)
1.3.2 How many water points are available on the Medihelp Stellenbosch Cycle tour? (2)
1.3.3 Which national road crosses the route? (2) 1.3.4 In which general direction is Stellenbosch from Pniel? (2)
1.3.5 Identify the mountain pass situated on the route. (2)
[20]
QUESTION 2
2.1
| Mr Salters travelled from East London to Johannesburg, via Bloemfontein, to deliver boxes of seed. The map below shows the national roads of South Africa. [Adapted from https://images.google.co.za] |
Use the map above to answer the questions that follow.
2.1.1 Identify the type of scale used on the map. (2)
2.1.2 Name only TWO national roads that Mr Salters will travel on from East London to Johannesburg via Bloemfontein. (2)
2.1.3 Write down the general directions that a person will travel from Cape Town to Garies, and from Garies to Upington. (2)
2.1.4 Mr Salters’ wife wishes to visit Walvis Bay in Namibia during the December holidays. Mr Salters comments that she would need a passport to go to Walvis Bay.
Give a reason why his wife will need a passport to visit Walvis Bay. (2)
2.1.5 The fuel tank of Mr Salters’ vehicle has a capacity of 75 litres. He claims that it will cost him 4% more if he fills his car inland, instead of at the coast.
| NOTE: Fuel cost: ➢ Inland: R22,49 ➢ Coastal: R21,77 [Source: AA Petrol price January 2024] |
Verify, with the necessary calculations, whether his claim is valid or not. (5)
2.2
| The Kruger National Park is a popular tourist destination. Some information about the park is given below: The speed limit inside the park is:
Gate times:
ANNEXURE B shows a part of a map of the Kruger National Park and TABLE 2 shows the distances between camps and gates. |
Use the information above and ANNEXURE B to answer the questions that follow.
2.2.1 Give ONE possible reason why there are specific times for the opening and closing of gates at the park. (2)
2.2.2 Determine the difference in the number of main camps and other camps on this part of the map. (2)
2.2.3 If Odwa leaves Skukuza at 17:15 and leaves the park through the Numbi Gate, determine the time that he will reach the Numbi Gate.
The following formula may be used:
Distance = speed × time
NOTE: The distance on the gravel road is the same as the distance on the tarred road. (5)
2.2.4 Give a possible reason why most people visiting the park prefer to travel on the gravel roads, instead of the tarred roads. (2) [24]
QUESTION 3
3.1
In a Mathematical Literacy classroom, a teacher keeps coloured pencils in three identical cylindrical containers. These pencils remain in the containers until they are used or lost. Below is an example of an image of the container with the coloured pencils and the diagram of the cylindrical container. (Diagram NOT drawn to scale.) | |
Example of image of container with coloured pencils | Diagram of cylindrical container with dimensions |
3.1.1 The diameter of one of the coloured pencils is 6 mm and the length is 16,7 cm. Verify, with the necessary calculations, that 39 coloured pencils can fit into THREE of the cylindrical containers. (9)
3.1.2 The teacher packs some of the coloured pencils as follows in each of the containers: 3 pink, 2 black, 2 purple and 3 orange pencils. Calculate the probability that if a coloured pencil is taken from ALL the containers, it will be a purple pencil. Give your final answer to THREE decimal places. (3)
3.2 Invitation cards for a party are in a rectangular shape, with a circular photo of the birthday girl in the middle of the invitation card. An example of the invitation card is given below and a diagram with dimensions.
| Example of image of invitation without photo | Diagram of invitation card with dimensions |
| | 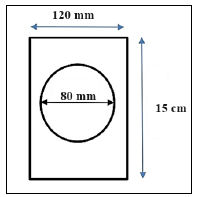 |
3.2.1 (a) Calculate the area of the rectangular invitation card to the nearest mm2.
You may use the following formula:
Area of a rectangle = length × width (3)
(b) Hence, calculate the area of the rectangular invitation card without the photo to the nearest mm2.
You may use the following formula:
Area of circle = π × radius2. Use π = 3,142 (4)
3.2.2
| One of the guests buys a gift that is packaged in a rectangular box as shown below. She must wrap the gift box with wrapping paper. Dimensions of the box are: Length = 38,8 cm Width = 27,5 cm Height = 30 cm |
Calculate the total surface area in cm2of the paper that is needed to wrap the gift box.
You may use the following formula:
Total Surface Area of gift box = 2 (length × width) + 2 (width × height) + 2 (length × height) (4)
3.3
Electricity has become a scarce resource in South Africa. As a result, the country is investigating alternative sources of generating electricity. One alternative source of generating electricity is a wind turbine using rotating blades as shown in the picture and diagram below. Image of wind turbine Diagram of wind turbine The wind turbine is mounted on the top of a 50 m high tower. The length of each blade is 31 m. |
3.3.1 Determine the length of the diameter of the circle that the blades create as they rotate. (2)
3.3.2 Calculate the maximum height from the ground to the tip of a blade if the turbine is rotating. (2)
3.3.3 Calculate the circumference of the circle made by the blades when it rotates twice.
You may use the following formula:
Circumference = 2 × π × radius, using π = 3,142 (2)
3.3.4 Suppose each household requires 25 kWh of electricity daily.
If one wind turbine produces 1 750 kWh of electricity daily, calculate how many households could be provided with electricity daily from one such turbine. (2)
3.4 Sandra washes her dishes by hand three times daily in TWO identical cylindrical basins. She uses one basin for washing the dishes and the other for rinsing it. Each basin has a radius of 30 cm and a depth of 45 cm, as shown in the diagram below.
| Cylindrical basin with dimensions Dimensions: Radius = 30 cm Height = 45 cm |
Sandra fills each basin to three quarters (¾) of its capacity whenever she washes or rinses the dishes.
Calculate how much water (in litres) she will use daily to wash and rinse dishes by hand. (NOTE: 1 000 cm3 = 1 litre)
You may use the following formula: Volume = π × r2 × h, use π = 3,142 (5) [36]
QUESTION 4
4.1
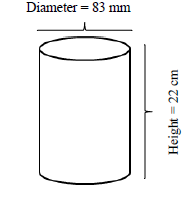
| Mr and Mrs Thana went shopping in Phuket, Thailand on Friday and checked into a hotel afterwards at 15:30. They departed from the hotel the following Tuesday at 10:00. They bought a small cylindrical gift box for their daughter to keep her earrings and hair accessories in, as shown below. d Dimensions: Diameter = 10 cm Height = 20 cm NOTE: Area of a circle = 3,142 × radius2 Volume of a cylinder = 3,142 × radius2 × height [Source: www.google.com ] |
4.1.1 Verify, with the necessary calculations that the total number of hours that Mr and Mrs Thana stayed in the hotel was less than 90 hours. (5)
4.1.2 The volume of their daughter’s cylindrical gift box is 1 571 cm3 with a diameter of 10 cm. Calculate the height of the cylindrical gift box. (4)
4.1.3 The top and the bottom of the cylindrical gift box is made of a special type of wood that costs R144,65/m2. Calculate the total cost of the wood to make the top and the bottom of the cylindrical gift box, if the area of the top is 78,55 cm2. (5)
4.2 Ms Harker asked a builder to draw a scale drawing of a proposed renovation to her house. The floor plan of the proposed renovation is shown below.
| |
4.2.1 The measured length of the main bedroom is 3,4 cm. Use the given scale to calculate the actual length of the main bedroom. (2)
4.2.2 What is the probability of selecting a door that opens to the eastern side? (2)
4.2.3 Given that the house is situated in South Africa, explain which room you think will get the most sun. (2) [20]
TOTAL: 100
MARKS: 100
Symbol | Explanation |
M | Method |
M/A | Method with accuracy |
CA | Consistent accuracy |
A | Accuracy |
C | Conversion |
S | Simplification |
RT/RG/RD/RM | Reading from a table/graph/diagram/map |
SF | Correct substitution in a formula |
O | Opinion/Explanation//Reasoning |
P | Penalty, e.g. for no units, incorrect rounding off etc. |
R | Rounding off |
NPR | No penalty for rounding |
AO | Answer only |
MCA | Method with consistent accuracy |
RCA | Rounding consistent with accuracy |
MARKING GUIDELINES
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- If a candidate has crossed out (cancelled) an attempt to a question and NOT redone the solution, mark the crossed out (cancelled version).
- Consistent Accuracy (CA) applies in ALL aspects of the marking guidelines; however, it stops at the second calculation error.
- If the candidate presents any extra solution when reading from a graph, table, layout plan and map, then penalise for every extra incorrect item presented.
KEY TO TOPIC SYMBOL: F = Finance; M = Measurement; MP = Maps, plans and other representations; P = Probability | |||
QUESTION 1 [20 MARKS] ANSWER ONLY FULL MARKS | |||
Ques. | Solution | Explanation | Level |
1.1.1 | The perimeter of a shape is the total distance around the edges defining the outline of that shape. ✓✓A OR Total distance around the shape. ✓✓A | 2A correct explanation
(2) | M L1 |
1.1.2 | Length of wall = 370/100 ✓C = 3,7 m ✓A | 1C convert cm to m 1A correct answer (2) | M L1 |
1.1.3 | P = length + length + height + height = 3,7 + 3,7 + 2,1 + 2,1 = 11,6 m ✓CA✓M | CA from 1.1.2 1M adding correct values 1CA correct answer from 1.1.2 (2) | M L1 |
1.2.1 | Distance cycled =75 / 0,6214 ✓MA = 120,6952044 ✓A ≈ 120,7 km Accept: 121 km / 120,695 km | 1MA dividing correct values 1A correct answer NPR (2) | M L1 |
1.2.2 | Total distance logged: = 120,7 km + 114,3 km + 271 km + 148,1 km ✓M = 654,1 km ✓CA Accept 654,4 km / 654,095 | CA from 1.2.1 1M adding correct values 1CA correct answer (2) | M L1 |
1.3.1 | Pniel ✓✓RT | 2RT reading from map (2) | MP L1 |
1.3.2 | 5 water points ✓✓RT | 2RT correct answer (2) | MP L1 |
1.3.3 | N1 ✓✓RT | 2RT correct answer (2) | MP L1 |
1.3.4 | SW or Southwest ✓✓RT | 2RT correct direction (2) | MP L1 |
1.3.5 | Helshoogte Pass ✓✓RT | 2RT correct answer (2) | MP L1 |
[20] | |||
QUESTION 2 [24 MARKS] | |||
Ques. | Solution | Explanation | Level |
2.1.1 | Bar Scale ✓✓A OR Linear Scale ✓✓A OR Graphic ✓✓AScale | 2A identifying correct scale (2) | MP L1 |
2.1.2 | N6 ✓RT and N1 ✓RT | 1RT first national road 1RT second national road Accept any order (2) | MP L1 |
2.1.3 | North ✓A North East OR NE ✓A | 1A first direction 1A second direction (2) | MP L2 |
2.1.4 | His wife will be crossing the border between two countries and therefore needs a passport. ✓✓O OR His wife will enter another country. ✓✓O | 2O opinion (2) | MP L4 |
2.1.5 | ✓M % difference = (R22,49 – R21,77) ÷ R21,77× 100% ✓M ✓A = 3,307% ✓CA Statement is invalid – it will cost less than 4% ✓O OR ✓M % difference = ((R22,49 × 75) – (R21,77 × 75)) ÷ (R21.77 × 75)× 100% ✓M ✓A = (1 686,75 – 1 632,75) ÷ 1 632,75 × 100% = 3,307% ✓CA Statement is invalid – it will cost less than 4%. ✓O | 1M subtracting correct values 1M multiplying with 100% 1A correct denominator 1CA simplification 1O opinion OR 1M subtracting correct values 1M multiplying with 100% 1A correct denominator 1CA simplification 1O opinion (5) | F L4 |
2.2.1 | Staff working at the gates need to go home. ✓✓O OR The wild animals in the park make it unsafe to travel or be in unprotected parts during the night. ✓✓O OR Animals are not visible in the dark, park/camp gates open when people can see the animals. ✓✓O OR Access control ✓✓O OR To avoid overcrowding ✓✓O OR Security reasons ✓✓O OR So that people travelling from far or within the Kruger National Park, can plan ahead. ✓✓O OR Accept any other valid reason. | 2O reason (2) | MP L4 |
2.2.2 | Other camps = 5 Main camps = 7 ✓RT Difference = 7 – 5 = 2 ✓CA | 1RT number of both camps 1CA difference with 1 correct camp AO (2) | MP L2 |
2.2.3 | Distance = speed × time ✓RT 54 km = 50 km/h × time ✓SF Time on gravel road follows do not = 54 km / 50 km/h ✓S = 1,08 h = 1h 4 min 48 sec ✓C Time he will arrive at the gate is: 17:15 + 1:4:48 = 18:19:48 ✓CA If calculated as 1h05min 17:15 + 1h05min = 18:20 | 1RT distance 1SF substitution with 50 km/h 1S change the formula 1C converting time 1CA arrival time (5) | MP L3 |
2.2.4 | The roads are not so busy / people drive slower / more animals are visible. ✓✓O OR It is the scenic route. ✓✓O OR To experience a sense of adventure. ✓✓O OR Gravel roads give you more access (short cut) to different parts of the park. ✓✓O OR The route blends in with nature and gives a more authentic bushveld experience. ✓✓O OR Accept any other reasonable answer. | 2O reason (2) | MP L4 |
[24] |
QUESTION 3 [36 MARKS] | |||
Ques. | Solution | Explanation | Level |
3.1.1 | Number of coloured pencils across = 83 ÷ 6 ✓M = 13,833333… ✓CA ≈ 13 pencils ✓R Number of coloured pencils down = 22 ÷ 16,7 ✓M = 1,317365269 ≈ 1 pencil ✓R Total number of pencils in one container = 13 × 1 = 13 pencils ✓CA Number of pencils in 3 containers = 13 × 3 ✓M = 39 pencils ✓CA ⸫ Correct ✓O | 1M dividing diameters 1CA simplification 1R number of pencils 1M dividing heights 1R number of pencils 1CA number of pencils in one container 1M multiply by 3 1CA total number of pencils 1O opinion (9) | M L4 |
3.1.2 | Probability of taking a purple pencil from a container ✓A = 6 / 39 ✓A = 0,153846153 ≈ 0,154 ✓R | CA from 3.1.1 1A numerator 1A denominator 1R 3 decimal places (3) | P L2 |
3.2.1 (a) | Area of rectangle = length × width = 150 mm × 120 mm = 18 000 mm2✓C ✓SF ✓A | 1C convert to mm 1SF substitution 1A area of rectangle (3) | M L2 |
(b) | Area of circle = π × radius2 = 3,142 × 402 ✓A = 5 027,2 mm2 ✓CA OR = 3,142 × 40 × 40 ✓A = 5 027,2 mm2 ✓CA Area without photo = 18 000 mm2– 5 027,2 mm2✓M = 12 972,8 mm2 ≈ 12 973 mm2✓CA | CA from 3.2.1 (a) 1A radius 1CA area of circle 1MCA subtracting two areas 1CA rounding to nearest mm2 (4) | M L3 |
3.2.2 | Surface area of gift box = 2 (length × width) + 2 (width × height) + 2 (length × height) = 2 (38,8 × 27,5) + 2 (27,5 × 30,0) + 2 (38,8 × 30,0) ✓SF✓A = 2 134 + 1 650 + 2 328 ✓S = 6 112 cm2 ✓CA | 1SF substitution 1A correct values 1S simplification 1CA surface area (4) | M L2 |
3.3.1 | Diameter = 31 m × 2 ✓M = 62 m ✓A | 1M multiply radius by 2 1A correct diameter (2) | M L2 |
3.3.2 | Maximum height = 50 m + 31 m = 81 m ✓MA ✓A | 1MA adding correct values 1A answer (2) | M L2 |
3.3.3 | Circumference = 2 × π x radius = 2 × 3,142 × 31 ✓SF = 194,804 × 2 = 389,608 m ✓MA | 1SF substitution 1MA multiply by 2 and answer NPR (2) | M L2 |
3.3.4 | Number of households = 1 750/25 ✓M = 70 households ✓A | 1M dividing by 25 1A correct answer (2) | M L1 |
3.4 | Volume of 2 cylindrical basins used three times a day = π × r2 × h ✓SF✓M = (3,142 × 302 × 45) × 2 × 3 = 763 506 cm3✓CA Litres of water used daily =763 506 / 1 000× ¾ ✓C = 572,6295 litres ✓CA OR Volume of 2 cylindrical basins used three times a day = π × r2 × h ✓SF✓M = (3,142 × 302 × 45) × 2 × 3 = 763 506 cm2 ✓CA Litres of water used daily = 763 506 × ¾ = 572 629,5 cm3 = 572 629,5 ✓C = 572,6295/1 000 litres ✓CA | 1SF substitution 1M multiplying by 2 and 3 1CA volume 1C converting to litres 1CA ¾ litres of water 1SF substitution 1M multiplying by 2 and 3 1CA volume of water 1C converting to litres 1CA ¾ litres of water (5) | M L3 |
[36] |
QUESTION 4 [20 MARKS] | |||
Ques. | Solution | Explanation | Level |
4.1.1 | Total number of hours: Friday: 24:00 – 15:30 = 8,5 hours ✓A Saturday – Monday = 24 hours × 3 days = 72 hours ✓A Tuesday = 10 hours ✓A Total number of hours = 8,5 + 72 + 10 = 90,5 hours ✓MA Invalid ✓O | 1A number of hours on Friday 1A number of hours for 3 days 1A number of hours on day of departure 1MA adding correct values and correct answer. 1O opinion (5) | M L4 |
4.1.2 | radius = diameter / 2= 10 / 2= 5 cm ✓A Volume of cylinder = 3,142 × radius2 × height 1 571 cm3 = 3,142 × 52 × height ✓SF Height = 1 571 / 78,55 ✓M Height = 20 cm ✓CA | 1A find radius 1SF substitution 1M change subject of the formula 1CA finding the height (4) | M L3 |
4.1.3 | Area of top and bottom surface = 78,55 cm2 × 2 ✓M = 157,1 cm2 ÷ 1002 ✓C = 0,01571 m2 ✓S Total cost = 0,01571 m2 × R144,65 ✓M = R2,27 ✓CA OR Area of top = 78,55 cm2 ÷ 1002 ✓C = 0,007855 m2 ✓S Cost of wood of top = 0,007855 × R144,65 ✓M = R1,13622575 Total cost = R1,13622575 × 2 ✓M = R2,27 ✓CA | 1M multiply by 2 1C divide by 1002 1S simplification of answer in m2 1M multiply R144,65 1CA answer OR 1C divide by 1002 1S simplification of answer in m2 1M multiply R144,65 1M multiply by 2 1CA answer (5) | F L3 |
4.2.1 | Actual length = 3,4 cm × 65 ✓M = 221 cm ✓A | 1M multiply correct values and correct answer 1A answer (2) | MP L2 |
4.2.2 | Probability = 3/7✓A | 1A numerator 1A denominator (2) | P L2 |
4.2.3 | The main bedroom. ✓A Room is facing north. ✓O | 1A correct room 1O opinion (2) | MP L4 |
[20] | |||
TOTAL: 100 | |||