GRADE 12 MATHEMATICS PAPER 1 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2016
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 12 questions.
- Answer ALL the questions.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will not necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise,
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTION 1
1.1 Solve for x:
1.1.1 x(x-7)=0 (2)
1.1.2 x? - 6x + 2 = 0 (correct to TWO decimal places) (3)
1.1.3 √x-1+1= x (5)
1.1.4 3x+3 - 3x+2 = 486 (4)
1.2 Given: ƒ(x)= x2 + 3x - 4
1.2.1 Solve for x if ƒ(x)=0 (2)
1.2.2 Solve for x if ƒ(x) <0 (2)
1.2.3 Determine the values of x for which ƒ'(x) ≥ 0 (2)
1.3 Solve for x and y: x=2y and x2- 5xy = -24 (4) [24]
QUESTION 2
Given the finite arithmetic sequence: 5;1; -3 ; ...; -83; -87
2.1 Write down the fourth term (T4) of the sequence. (1)
2.2 Calculate the number of terms in the sequence. (3)
2.3 Calculate the sum of all the negative numbers in the sequence. (3)
Consider the sequence: 5;1; -3; ...; -83; -87 ; ...; 4187 Determine the number of terms in this sequence that will be exactly divisible by 5. (4) [11]
QUESTION 3
3.1 The first four terms of a quadratic number pattem are -1 ; x ;3 x+8
3.1.1 Calculate the value(s) of x. (4)
3.1.2 If x=0, determine the position of the first term in the quadratic number pattem for which the sum of the first n first differences will be greater than 250. (4)
3.2 Rectangles of width 1 cm are drawn from the edge of a sheet of paper that is 30 cm long such that there is a 1 cm gap between one rectangle and the next. The length of the first rectangle is 21 cm and the length of each successive rectangle is 85% of the length of the previous rectangle until there are rectangles drawn along the entire length of AD. Each rectangle is coloured grey.
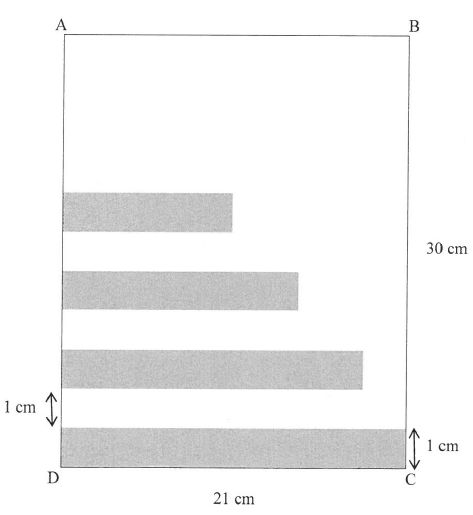
3.2.1 Calculate the length of the 10" rectangle. (3)
3.2.2 Calculate the percentage of the paper that is coloured grey.(4) [15]
QUESTION 4
Sketched below is the graph of h(x)= ax, a > 0. R is the y-intercept of h. The points P(2:9) and 06: lie on h.
The points P(2;9) and 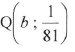 lie on h
lie on h
4.1 Write down the equation of the asymptote of h. (1)
4.2 Determine the coordinates of R. (1)
4.3 Calculate the value of a.(2)
4.4 D is a point such that DQ || y-axis and DP || x-axis. Calculate the length of DP. (4)
4.5 Determine the values of k for which the equation h(x + 2) + k = 0 will have a root that is less than -6. (3) [11]
QUESTION 5
Sketched below is the parabola ƒ, with equation with equation ƒ(x) = -x2 + 4x - 3 and a hyperbola g, with equation (x-p) (y +1)= 3.
- B, the turning point off, lies at the point of intersection of the asymptotes of g. A(-1;0) is the x-intercept of g.
- A (-1;0) is the x-intercept of g

5.1 Show that the coordinates of B are (2:1) (2)
5.2 Write down the range of ƒ. (1)
5.3 For which value(s) of x will g(x)≥0? (2)
5.4 Determine the equation of the vertical asymptote of the h(x) = g(x+4) (1)
5.5 Determine the values of p and t. (4)
5.6 Write down the values of x for which ƒ(x).g' (x) ≥ 0 (4) [14]
QUESTION 6
Given: ƒ(x) = -x+3 and g(x) = log2 x
6.1 On the same set of axes, sketch the graphs of ƒ and g, clearly showing ALL intercepts with the axes. (4)
6.2 Write down the equation of g-1(x), the inverse of g, in the form y=...(2)
6.3 Explain how you will use QUESTION 6.1 and/or QUESTION 6.2 to solve the equation log2 (3-x)= x. (3)
6.4 Write down the solution to log2 (3 - x)= x (1) [10]
QUESTION 7
On 1 June 2016 a bank granted Thabiso a loan of R250 000 at an interest rate of 15% p.a. compounded monthly, to buy a car. Thabiso agreed to repay the loan in monthly instalments commencing on 1 July 2016 and ending 4 years later on 1 June 2020. However, Thabiso was unable to make the first two instalments and only commenced with the monthly instalments on 1 September 2016.
7.1 Calculate the amount Thabiso owed the bank on 1 August 2016, a month before he paid his first monthly instalment. (2)
7.2 Having paid the first monthly instalment on 1 September 2016, Thabiso will still pay his last monthly instalment on 1 June 2020. Calculate his monthly instalment. (4)
7.3 If Thabiso paid R9 000 as his monthly instalment starting on 1 September 2016, how many months sooner will he repay the loan? (5)
7.4 If Thabiso paid R9 000 as a monthly instalment starting on 1 September 2016, calculate the final instalment to repay the loan. (4) [15]
QUESTION 8
8.1 Determine ƒ'(x) from first principles if ƒ(x) = 3x2 (5)
8.2 John determines g'(a), the derivative of a certain function g at x = a, and arrives at the answer:![]()
Write down the equation of g and the value of a. (2)
8.3 Determine 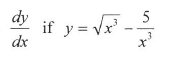 (4)
(4)
8.4 g(x)= -8x + 20 is a tangent to ƒ(x)= x3 + ax2 + bx +18 at x = 1. Calculate the values of a and b. (5) [16]
QUESTION 9
For a certain functions, the first derivative is given as ƒ'(x)=3x2 +8x - 3
9.1 Calculate the x-coordinates of the stationary points of ƒ (3)
9.2 For which values of x is ƒ concave down? (3)
9.3 Determine the values of x for which ƒ is strictly increasing (2)
9.4 If it is further given that ƒ(x) = ax3 + bx2 + cx+d and ƒ(0) = -18, determine the equation of ƒ. (5) [13]
QUESTION 10
The number of molecules of a certain drug in the bloodstream t hours after it has been taken is represented by the equation M(t)= -t3 +3t2 +72t, 0<t<10.
10.1 Determine the number of molecules of the drug in the bloodstream 3 hours after the drug was taken. (2)
10.2 Determine the rate at which the number of molecules of the drug in the bloodstream is changing at exactly 2 hours after the drug was taken. (3)
10.3 How many hours after taking the drug will the rate at which the number of molecules of the drug in the bloodstream is changing, be a maximum? (3) [8]
QUESTION 11
A survey was conducted among 100 boys and 60 girls to determine how many of them watched TV in the period during which examinations were written. Their responses are shown in the partially completed table below.
| WATCHED TV DURING EXAMINATIONS | DID NOT WATCH TV DURING EXAMINATIONS | TOTALS | |
| Male | 80 | a | |
| Female | 48 | 12 | |
| Totals | b | 32 | 160 |
11.1 Calculate the values of a and b. (2)
11.2 Are the events "being a male' and 'did not watch TV during examinations' mutually exclusive? Give a reason for your answer. (2)
11.3 If a learner who participated in this survey is chosen at random, what is the probability that the learner:
11.3.1 Watched TV in the period during which the examinations were written? (2)
11.3.2 Is not a male and did not watch TV in the period during which examinations were written? (2) [8]
QUESTION 12
The digits 1 to 7 are used to create a four-digit code to enter a locked room. How many different codes are possible if the digits may not be repeated and the code must be an even number bigger than 5 000? [5]
TOTAL: 150
